證明Multiset等價其實也是一種置換證明，為什麼這樣說呢?
因為在上一篇的例子中證明Multiset等價就表示存在兩個向量具有一個可證明的置換關係。
假設兩個向量分別是向量q和向量p:

而當兩個向量具有一個可證明的置換關係時，就是它們各自所包含的元素是相同的，只是排列的次序不同。
舉一個例子，假設向量q和向量p是存在一個奇偶位置的互換關係，就是向量q中偶數位置的元素與向量p中奇數位置的元素是相同的，
所以進行互換後是不影響，換角度去思考，兩個向量是有相同的元素，要是把其中一個向量的元素重新排列。為了進行計算，需要將向量通過多項式編碼把向量轉換為多項式。
首先假設向量q存在n個元素，當中的元素排列以向量i表示，而向量p也存在n個元素，當中的元素排列以y(i)表示。
然後可以把向量q、向量i、向量p、y(i)按行列的形式展示出來:
在圖表中可以看到第一行，q0的index是0，p0的index是1, 所以p0會等於q1。第二行，q1的index是1，p1的index是0, 所以p1會等於q0。
由此，看到它們進行了奇偶位置互換。
然後，可以再進一步簡化圖表，將左邊的兩列合併在一起，還有將右邊的兩列合併在一起。
從而轉換成新的圖表如下: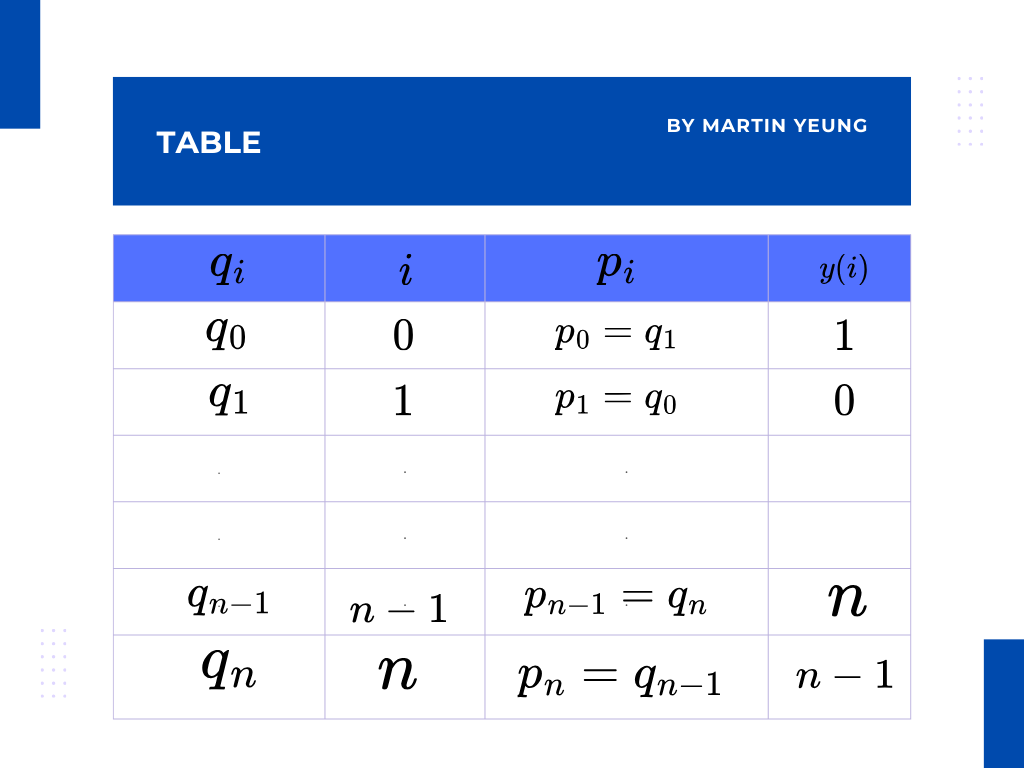

所以只要滿足y(i)的置換，就可以說明向量q和向量p是存在一個Multiset的等價關係。
到了這一步，相信大家都會思考以上的證明存在什麼意思?
其實想透過向量和位置的合併，表示可以通過一個置換證明來把公式轉換為一個多重集合的證明，所以可以更進一步地說，只要置換證明能轉換為一個多重集合就可以避免為特定的置換條件再進行額外證明。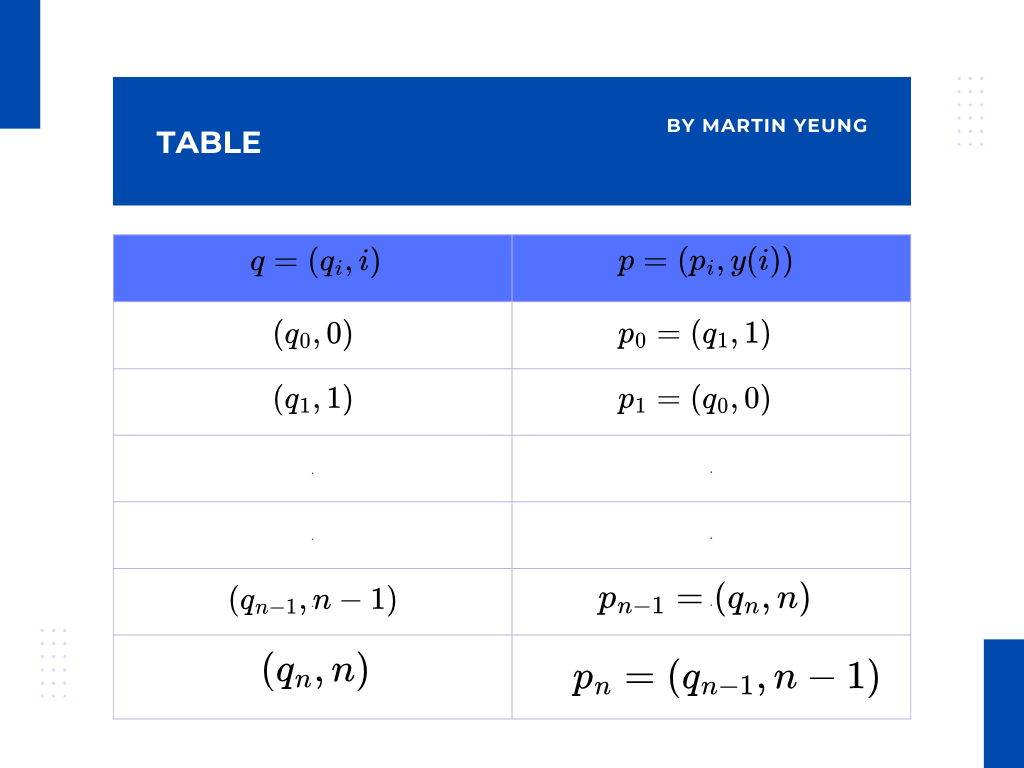

雖然解決到證明的條件，但現在的情況是沒辦法將兩組條件(即向量q和向量i)整合為一個一元多項式的根集合，為了應對這問題，就需要使用到一個技巧，就是從驗證者取到一個隨機數B，然後利用這隨機數與向量i結合再加上向量q而生成一個新的值，如下圖所示: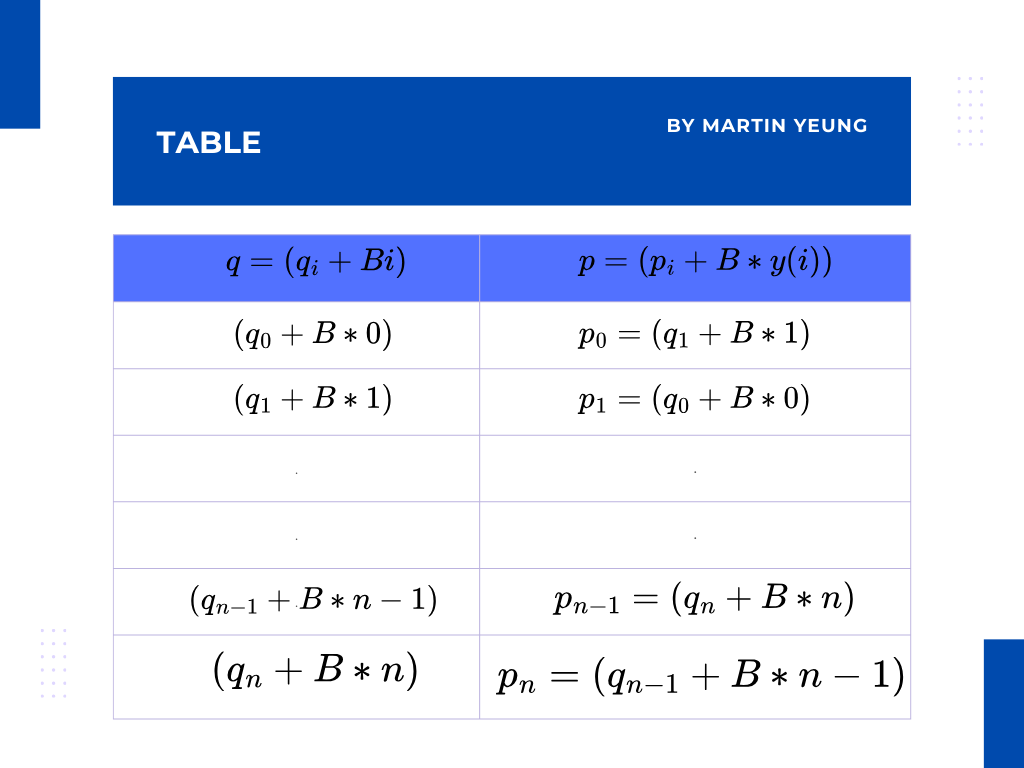

證明者在獲得隨機數B後，再利用它來生成對向量q和向量p的等價證明。

完整的置換證明
0. 必須要準備以下東西
0.1 公共輸入: 置換關係y , y 是一種置換方案，例如奇偶置換
0.2 秘密輸入: 兩個向量q和p
0.3 預先處理: 證明者和驗證者所創建的id(X)及y(X)

1. 證明者創建及發送q(X)及p(X)給驗證者
2. 驗證者向證明者挑戰，包含隨機數B (會用於進行多個數值的整合)和隨機數γ (會用於求值的)
3. 證明者創建一個輔助向量，用於組成多項式，及生成證明發送給驗證者
   
4. 驗證者會發送挑戰隨機數y
5. 證明者創建一個f(X)及r(X)，然後發送r(x)證明給驗證者
   
6. 驗證者會向q(X), p(X), r(X)求在X=δ的值，從而得到q(δ), p(δ), r(δ)。另外，也會在z(X)上分別求取X在δ和w上的值。
   而在y(X)和id(X)上X=δ的值也會用於驗證者的計算，公式如下:
   

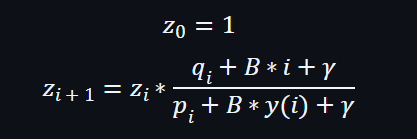
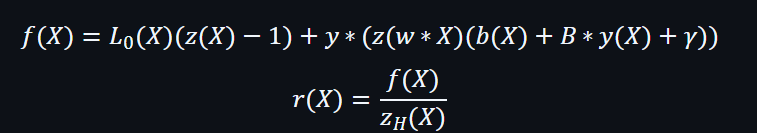
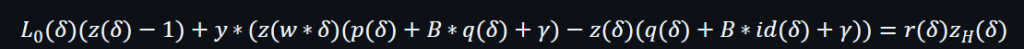
只要通過驗證，就表示證明是真確的。