多項式承諾 (Polynomial Commitment Scheme)

什麼是承諾呢? 就是證明者不可以改變產生承諾所運用的計算的多項式，證明者只能夠對一個多項式提供有效的證明。如果無法提供相關證明或者證明被驗證者拒絕時，這就不是承諾，而是這假。從另一角度說，承諾就是對某一件事的保證，例如數值不變、公式不變、結果不變等。

在多項式承諾中，承諾的值與對象是存在兩個必然關係。

1. 隱藏關係(Hiding):
   是指承諾的值不會透露任何關於對象的資料。
2. 綁定關係(Binding):
   是指不會找到另一個與對象相等的東西。

承諾的例子有很多，最簡單的承諾就是Hash的結果，當一項資料通過Hash運算之後就會產出一個Hash值，
而這個值是不會透露資料的內容，而且更是與資料綁定，所以不會有其他資料能產出相同的Hash值，只有相同的資料才可以產出同一Hash值。

在多項式承諾中是怎樣進行承諾呢?
首先，假設有一個多項式如下: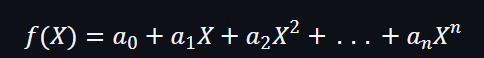

之後將多項式中的所有系數都標示出來，然後進行Hash運算，從而獲得一個數值，這個數值與多項式之間是存在一個綁定關係(Binding)。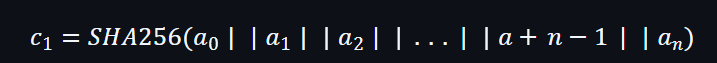

當然，除了Hash運算，還有其他承諾方式，在往後會再討論。
回到多項式承諾，當證明者成功創建多項式承諾後，驗證者就可以基於這個承諾，對產出承諾的多項式進行驗證，
只要向證明者發出一個挑戰，讓證明者在多項式上對某個值進行計算，從而檢查證明者所計算的值是否正確。

假設:
C = Commit(f(X))
驗證者能夠向提出承諾證明的證明者發出一個挑戰，去檢查多項式在X=δ的值，這個時候，證明者需要回覆一個y值，y表示f(X)的值。
同時也需要提供一個證明用於為自己回覆的y值的正確性作證明。

多項式承諾可以被當作是一個輕量級的可驗證計算工具，由原來驗證者的工作(多項式的運算)轉移到去證明者的手中，所以能大大減少驗證者的工作量。另外，多項式承諾更可以用於私隱證明，證明者可以在不透露隱私的情況下證明某些事件的正確性。
在目前，存左各種多項式承諾方法，各有特色，例如: IPA, Pedersen, KZG10, FRI, Dark, Dony 等等的方案。

參考資料:

1. Inner Product Argument (IPA) and a Polynomial Commitment Scheme
   https://blog.lambdaclass.com/ipa-and-a-polynomial-commitment-scheme/