在這篇文章中，我將討論前綴和（prefix sum）

前綴和

有一個整數陣列 nums[:n]，那麼前綴和 prefix[i] 代表的是陣列中從第 0 個元素到第 i 個元素的總和。prefix[i] 用數學公式表達為：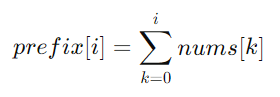

簡單說，prefix[i] 是陣列 nums 前 i 項的總和。

假設 nums = [2, 3, 7, 1]，那麼對應的前綴和序列 prefix 為：

prefix[0] = 2 （因為只加上了第一個數）
prefix[1] = 2 + 3 = 5
prefix[2] = 2 + 3 + 7 = 12
prefix[3] = 2 + 3 + 7 + 1 = 13

因此 prefix = [2, 5, 12, 13]

303. Range Sum Query-Immutable (easy)

主題: 一維的區間和查詢

題目:
給定一個整數數組 nums，有個函式能夠計算索引 left 和 right 之間的 nums 元素的總和。（即 nums[left] + nums[left + 1] + ... + nums[right]）。

我寫法:
我的前綴和與標準前綴和不同。prefix[0] 是保留空間，prefix[i+1] 等於 nums[0] 到 nums[i] 的總和，這樣讓我直接用 prefix[right+1] - prefix[left] 算區間和，而不用 prefix[right] - prefix[left-1]且還要額外處理 left 為 0 的情況。

假若 nums = [2, 3, 7, 1]，那麼 prefix = [0, 2, 5, 12, 13]

以下用 Rust 解題:

struct NumArray {
    prefix: Vec<i32>,
}

impl NumArray {

    fn new(nums: Vec<i32>) -> Self {
        let mut prefix = vec![0; nums.len()+1];
        for i in 0..nums.len() {
            prefix[i+1] = prefix[i] + nums[i];
        }
        Self { prefix }
    }
    
    fn sum_range(&self, left: i32, right: i32) -> i32 {
        return self.prefix[right as usize +1] - self.prefix[left as usize];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * let obj = NumArray::new(nums);
 * let ret_1: i32 = obj.sum_range(left, right);
 */

我對圖論題目相對不熟很多，因此需要比較多的時間練習並寫成文章，預計下周後再繼續寫圖論相關的題目。