線段樹

線段樹是一種二元樹形的資料結構。它將陣列劃分為多個區間，並在每個節點中存儲對應區間的資訊（例如區間總和、最小值、最大值等）。

線段樹的特點：

• 節點結構：每個節點表示一個區間 [l, r]，並存儲該區間的相關資訊。
• 葉節點：區間縮小為單個元素時（即 l == r），該節點為葉節點，直接存儲陣列中的元素值。
• 內部節點：其值由左子樹和右子樹的值組合而成，例如，區間總和樹的內部節點值為其左子樹和右子樹的總和。

線段樹範例: (圖片來源)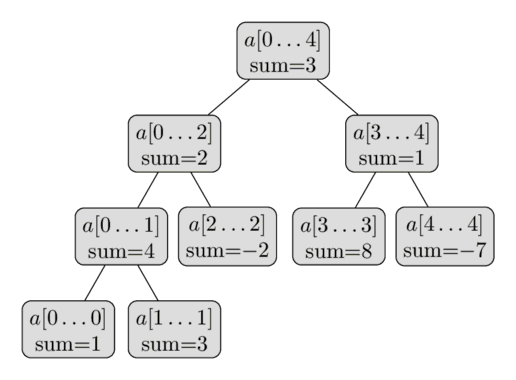

適用場景：

• 多次區間查詢：如區間總和、區間最小值、區間最大值等。
• 區間更新：單點更新或區間更新操作。

線段樹 vs. 前綴和與差分陣列

• 線段樹所有操作(區間查詢、區間修改)是 O(log N) (樹高)

• 前綴和 區間查詢: O(1)
• 差份陣列 區間修改: O(1)

我第14篇寫了前綴和、第16篇介紹了 差分陣列，有興趣的人能看看

307. Range Sum Query - Mutable (Medium)

題目要求:
給一個整數陣列 nums，實作 NumArray 類別：

• NumArray(int[] nums) 使用整數陣列 nums 初始化物件。
• void update(int index, int val) 將 nums[index] 的值更新為 val。
• int sumRange(int left, int right) 傳回索引 left 和 right 之間的 nums 元素的總和（即 nums[left] + nums[left + 1] + ... + nums[right]）。

解題想法:

• 構建線段樹：遞歸地將數組劃分為左右兩部分，直到區間縮小為單個元素，並在每個節點存儲對應區間的總和。
• 更新操作：在線段樹中查找到需要更新的葉節點，更新其值，並向上遞歸地更新受影響的父節點的總和。
• 區間和查詢：根據查詢的區間，在線段樹中遞歸查詢左子樹和右子樹，並累加結果。

struct SegmentNode {
    int sum, l, r;
    SegmentNode *left;
    SegmentNode *right;
    SegmentNode(int sum, int l, int r) {
        this->sum = sum;
        this->l = l;
        this->r = r;
        left = NULL;
        right = NULL;
    }   
};

class NumArray {
public:
    SegmentNode* root;
    SegmentNode* buildTree(vector<int>&nums, int l, int r) {
        if(l == r) {
            return new SegmentNode(nums[l], l, r);
        }
        if (l > r) return NULL;
        int mid = l + (r - l) / 2;
        SegmentNode *tmp = new SegmentNode(0, l, r);
        tmp->left = buildTree(nums, l, mid);
        tmp->right = buildTree(nums, mid+1, r);
        tmp->sum = tmp->left->sum + tmp->right->sum;
        return tmp;
    } 
    NumArray(vector<int>& nums) {
        root = buildTree(nums, 0, nums.size()-1);
    }
    
    SegmentNode* update(SegmentNode* ptr, int index, int val) {
        if (ptr->l == index && ptr->r  == index) {
            ptr->sum = val;
            return ptr;
        }
        int mid = ptr->l + (ptr->r - ptr->l) / 2;
        // decide to recurse left or right
        if (index <= mid) {
            update(ptr->left, index, val);
        }
        else {
            update(ptr->right, index, val);
        }
        ptr->sum = ptr->left->sum + ptr->right->sum;
        return ptr;
    }

    void update(int index, int val) {
        SegmentNode* ptr = root;
        update(ptr, index, val);       
    }
    
    int sumRange(SegmentNode* ptr, int left, int right) {
        if (ptr->l == left && ptr->r == right) {
            return ptr->sum;
        }
        int mid = ptr->l + (ptr->r - ptr->l) / 2;
        
        // The query interval spans the left and right subtrees
        if (left <= mid && right > mid) 
            return sumRange(ptr->left, left, mid) + sumRange(ptr->right, mid+1, right);
        // The entire query range is in the left subtree
        else if (right <= mid)
            return sumRange(ptr->left, left, right);
        // The entire query range is in the right subtree
        else 
            return sumRange(ptr->right, left, right);
    }
    int sumRange(int left, int right) {
        SegmentNode* ptr = root;
        return sumRange(ptr, left, right);
    }
};

時間複雜度:
構建線段樹：O(N)，其中 N 為數組的長度。
更新操作：O(log N)，因為每次遞迴將區間劃分為一半。
區間查詢：O(log N)，同樣是因為遞歸劃分區間