Bellman-Ford 同源最短路徑演算法

Bellman-Ford 演算法和 Dijkstra 演算法一樣，都依賴於「鬆弛操作（relaxation）」來逐步縮短各節點的最短路徑 的同源最短路徑。

Bellman-Ford 的轉移方程式如下：

dp[to] = min(dp[src] + adj[src][to], dp[to]);

它的核心思想是反覆更新所有邊，若某邊的權重能使得目標節點的最短路徑變短，則更新該節點的距離，這稱之為一次「鬆弛」。

原本的 Bellmon ford 是跑 將全部的邊跑 V-1 次轉移式，倘若能讓原本的邊變短，那就是成功的relaxation了

至於為甚麼是 V-1 次

為甚麼 做 V-1次迭代?

那就要想到最差情況，假設這張圖是一直線，而 src 與 dst 是最遠的兩節點

[0]  -> [1]  -> [2] ... [N]

最一開始，所有節點到 src 除了 src 自己以外的最短路徑都是無窮大 (未知的意思)。
我每次做一次 relaxtion，就相當於 從 src 與向外多一邊的節點 (同心圓般擴散)得的最短路徑。而src 與 dst 最遠差V-1條邊。

787. Cheapest Flights Within K stops

問題描述: 給一個整數n，代表有 n 個城市，另外還有一個陣列 flights，代表班機飛次i = [起飛城市i, 降落城市i，價格i]
要求算出，從起飛城市 src 到降落城市dst ，並且要求最多經城市的個數k後最便宜的機票價格。

解題想法:
城市是節點，路徑權重是價格，而最便宜的價格即是最短路徑。

因此 Bellman ford 的演算法的逐步 relaxation的概念，就很適合套用到的這問題，但不用 V-1 求全部節點的最短路徑，而就只要從 src 向外擴展 k+1 條邊。

題目中的輸入輸出範例:

Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1

Output: 700

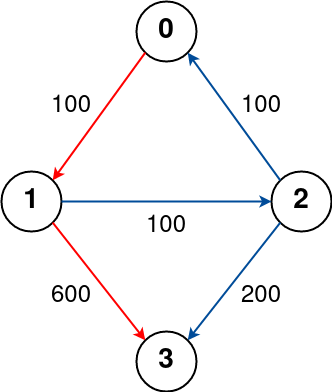
根據以上的Bellmon ford 的逐步鬆弛過程概念，各節點距離起點的最短距離(dp)逐步的更新會是:

src = 0
初始的 dp = [0, INF, INF, INF]
向 src 外走一條邊的 dp = [0, 100, INF, INF]
向外再走一條邊的 dp =  [0, 100, 100+100, 100+600] 

以下是我根據以上想法但有錯誤的程式碼:

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> dp(n, INT_MAX);
        dp[src] = 0;

        for (int i = 0; i < k; i++) {
            for (auto e: flights) {
                int from = e[0], to = e[1], weight = e[2];
                if (dp[from] != INT_MAX) {
                    dp[to] = min(dp[to], dp[from] + weight);
                }
            }
        }
        return dp[dst];
    }
};

當輸入: [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]]
,src = 0, dst = 3,k = 1

dp 變成 [0, 100, 200, 400] 與我以上預期的 dp = [0, 100, 200, 700] 不同

錯誤原因在於，是同一個迭代中的 dp 更新會影響到後續的計算，導致過早更新一些節點的值。

因此，我多引入一個 tmp_dp 陣列，避免同一輪迭代中的更新影響當前計算

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> dp(n, INT_MAX);
        dp[src] = 0;
        for (int i = 0; i <= k; i++) {
            vector<int>tmp_dp = dp;
            for (auto e: flights) {
                int from = e[0], to = e[1], weight = e[2];
                if (dp[from] != INT_MAX) {
                    tmp_dp[to] = min(tmp_dp[to], dp[from] + weight);
                }
            }
            dp = tmp_dp;
        }
        return dp[dst] == INT_MAX? -1: dp[dst];
    }
};

此版本的
runtime : 150ms Beats 5.01%
memory: 53.38MB Beats 5.00%

多做一個優化，加一個 updated的變數，在每次鬆弛操作後檢查是否有任何更新發生。如果沒有任何更新，則提前結束迭代，以節省不必要的計算：

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<int> dp(n, INT_MAX);
        dp[src] = 0;

        for (int i = 0; i <= k; ++i) {
            bool updated = false;
            vector<int> tmp_dp = dp;
            for (auto& e : flights) {
                int from = e[0], to = e[1], weight = e[2];
                if (dp[from] != INT_MAX && dp[from] + weight < tmp_dp[to]) {
                    tmp_dp[to] = dp[from] + weight;
                    updated = true;
                }
            }
            if (!updated) break; // Early stop if no updates
            dp = tmp_dp;
        }

        return dp[dst] == INT_MAX ? -1 : dp[dst];
    }
};

複雜度有提升!
Runtime: 19ms Beats 37.57%
Memory: 16.24MB Beats97.34%