再過去的幾節中我們進星了基礎的機器學習在股價上的探討，在本節中，我們將深入探討時間序列預測，特別是應用於金融市場的預測。時間序列預測在量化金融中扮演著重要的角色，能夠幫助我們預測未來的價格走勢、收益率等。首先，我們將了解時間序列分析的基本概念，如自相關、差分和穩定性等。接著，我們將學習如何使用ARIMA和Prophet等模型進行時間序列預測，並在實際的股票數據中進行應用。深度學習的部份將於下一節去介紹。今日 Colab

一、時間序列分析基礎

1. 時間序列的特點

時間序列是一組按時間順序排列的觀測值，通常具有以下特點：

• 趨勢（Trend）：數據隨時間的長期上升或下降趨勢。
• 季節性（Seasonality）：數據在固定週期內的反復模式。
• 週期性（Cyclical）：數據在不固定週期內的波動。
• 隨機性（Randomness）：數據中無法解釋的隨機波動。

2. 自相關與偏自相關

• 自相關函數（ACF）：衡量時間序列與其滯後值之間的相關性。

  

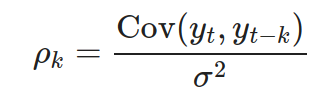
• 偏自相關函數（PACF）：衡量時間序列與其滯後值之間的純相關性，排除了中間滯後值的影響。

3. 平穩性

• 平穩時間序列：統計特性（均值、方差、自相關等）隨時間保持不變。
• 非平穩時間序列：統計特性隨時間變化，需要進行轉換（如差分）以使其平穩。

4. 差分

• 一階差分：用於消除序列的趨勢，使序列平穩。

  

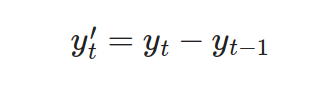
• 二階差分：對一階差分後的序列再進行差分，消除更高階的趨勢。

二、ARIMA模型

1. 模型介紹

• ARIMA模型（自回歸整合移動平均模型）是處理時間序列數據的常用模型。

• 模型組成：

  • AR（AutoRegressive，自回歸）部分：使用過去的值來回歸當前值。

    

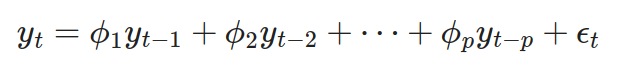
  • I（Integrated，整合）部分：通過差分使非平穩序列變為平穩序列。

  • MA（Moving Average，移動平均）部分：使用過去的誤差項來回歸當前值。

    

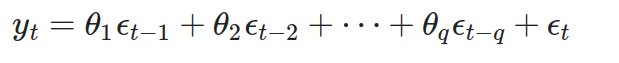
• ARIMA(p, d, q)：

  • p：自回歸項的數量。
  • d：差分次數。
  • q：移動平均項的數量。

2. ARIMA模型的構建流程

1. 檢查平穩性：使用ADF（Augmented Dickey-Fuller）單位根檢驗。

2. 差分處理：對非平穩序列進行差分，直到序列平穩。

3. 確定模型參數（p, d, q）：

   • ACF圖：用於選擇q值。
   • PACF圖：用於選擇p值。

4. 模型訓練與預測。

3. Python實現

(1) 數據準備

import pandas as pd
import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt

# 獲取股票數據
data = yf.download('AAPL', start='2015-01-01', end='2021-01-01')

# 提取收盤價
close = data['Adj Close']

(2) 檢查平穩性

from statsmodels.tsa.stattools import adfuller

# 原始序列的ADF檢驗
result = adfuller(close)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

# 繪製原始數據
plt.figure(figsize=(10,6))
plt.plot(close)
plt.title('原始收盤價時間序列')
plt.show()

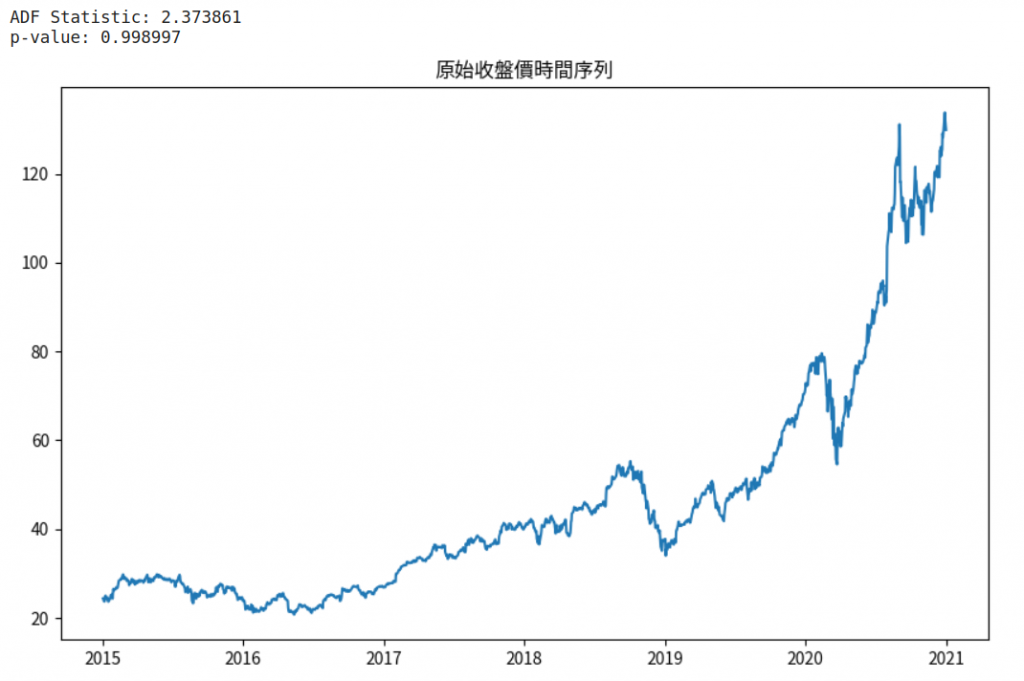
解釋：

• ADF檢驗：如果p-value > 0.05，則序列非平穩。

(3) 差分處理

# 一階差分
close_diff = close.diff().dropna()

# 差分後序列的ADF檢驗
result = adfuller(close_diff)
print('ADF Statistic after differencing: %f' % result[0])
print('p-value after differencing: %f' % result[1])

# 繪製差分後的數據
plt.figure(figsize=(10,6))
plt.plot(close_diff)
plt.title('一階差分後的收盤價時間序列')
plt.show()

(4) 確定p和q值

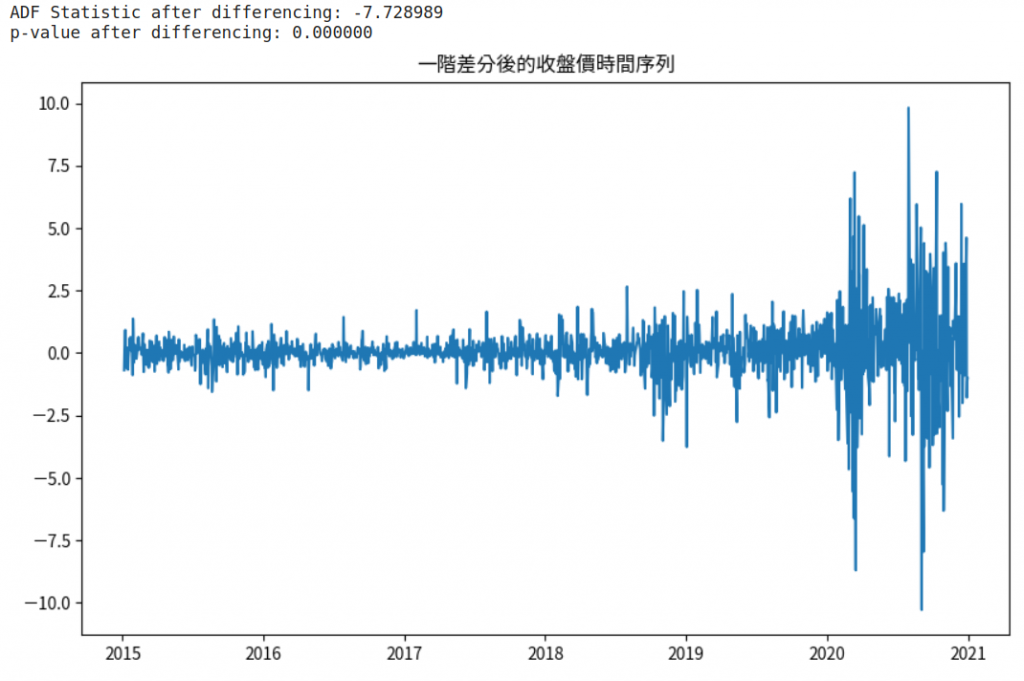
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 繪製ACF和PACF圖
fig, axes = plt.subplots(1,2, figsize=(16,4))
plot_acf(close_diff, lags=20, ax=axes[0])
plot_pacf(close_diff, lags=20, ax=axes[1])
plt.show()

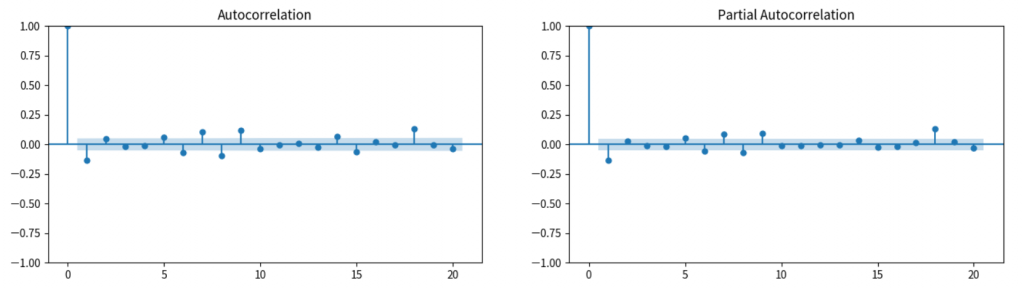
解釋：

• ACF圖：觀察滯後值與序列的相關性，用於確定q值。
• PACF圖：觀察滯後值與序列的偏相關性，用於確定p值。

(5) 建立ARIMA模型

from statsmodels.tsa.arima.model import ARIMA

# 設定模型參數 (p, d, q)
p = 5
d = 1
q = 5

# 建立並訓練模型
model = ARIMA(close, order=(p, d, q))
model_fit = model.fit()
print(model_fit.summary())

(6) 模型診斷

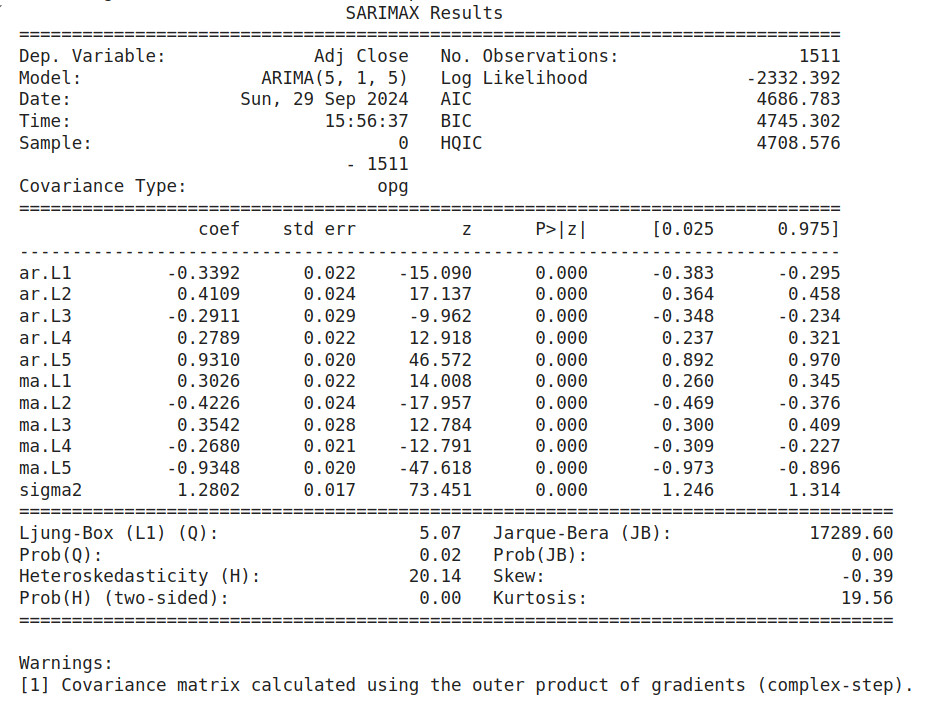
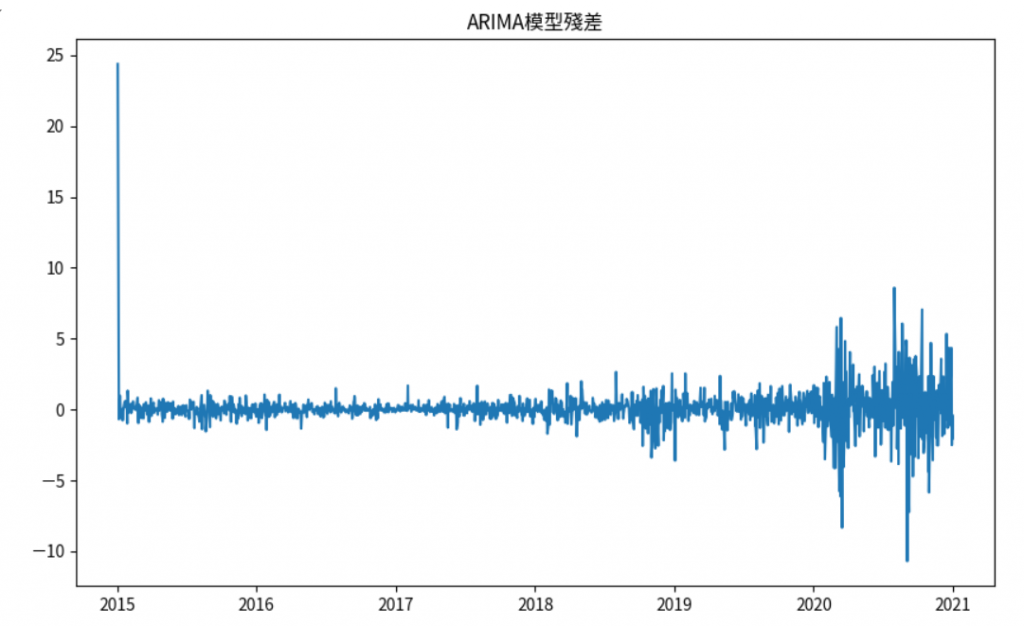
# 檢查殘差是否為白噪聲
residuals = model_fit.resid

# 繪製殘差圖
plt.figure(figsize=(10,6))
plt.plot(residuals)
plt.title('ARIMA模型殘差')
plt.show()

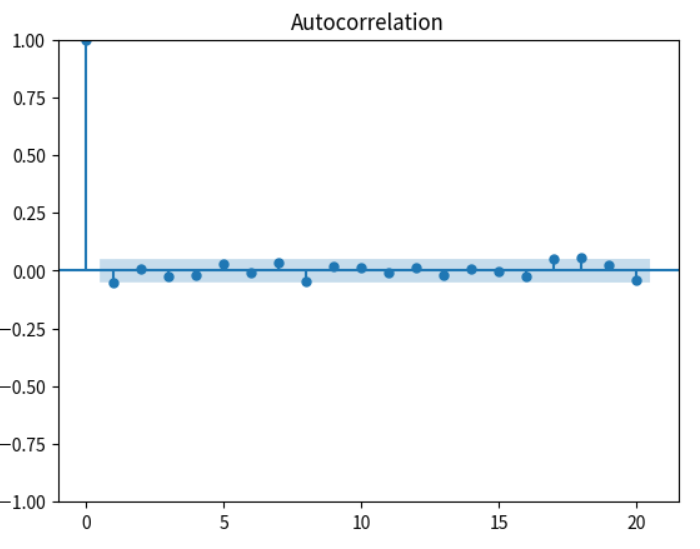
# 殘差的ACF圖
plot_acf(residuals, lags=20)
plt.show()

(7) 預測

# 預測未来 30 天
forecast_steps = 30
forecast_result = model_fit.get_forecast(steps=forecast_steps)

# 獲取預測均值
forecast_series = forecast_result.predicted_mean

# 獲取信賴區間
confidence_intervals = forecast_result.conf_int()

# 創見預測日期 Index
last_date = close.index[-1]
forecast_dates = pd.date_range(start=last_date + pd.Timedelta(days=1), periods=forecast_steps, freq='B')

# 設置預測的 index
forecast_series.index = forecast_dates
confidence_intervals.index = forecast_dates

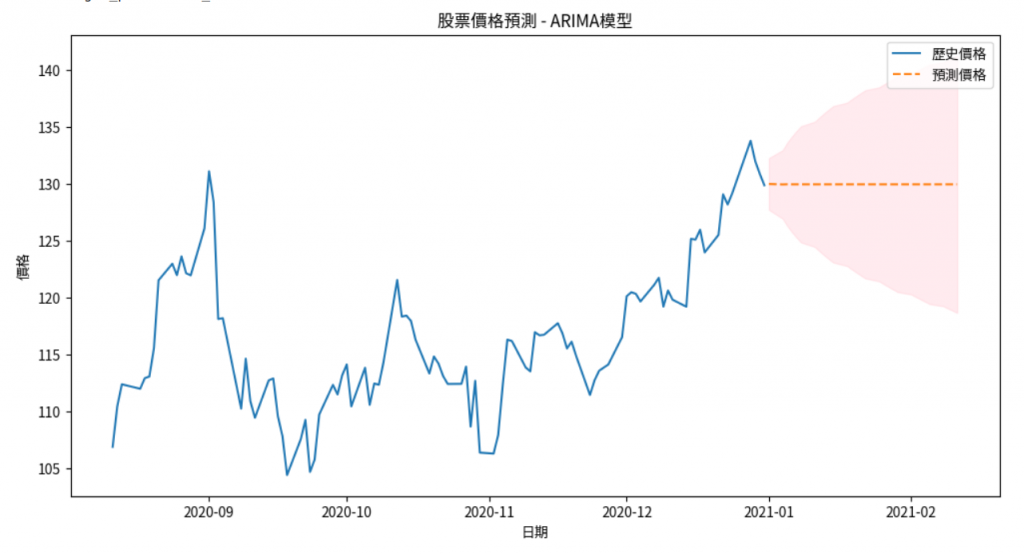
# 繪製預測結果
plt.figure(figsize=(12,6))
plt.plot(close[-100:], label='歷史價格')
plt.plot(forecast_series, label='預測價格', linestyle='--')
plt.fill_between(forecast_dates, confidence_intervals.iloc[:, 0], confidence_intervals.iloc[:, 1], color='pink', alpha=0.3)
plt.title('股票價格預測 - ARIMA模型')
plt.xlabel('日期')
plt.ylabel('價格')
plt.legend()
plt.show()

三、Prophet模型

1. 模型介紹

• Prophet 是由Facebook開發的開源時間序列預測工具，特點是簡單易用，適合具有明顯趨勢和季節性的時間序列數據。

• 模型組成：

  

  • g(t)：趨勢函數，模型長期變化。
  • s(t)：季節性函數，反映週期性變化。
  • h(t)：節假日效應。
  • epsilon_t：誤差項。

2. Python實現

(1) 安裝和導入

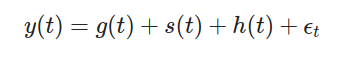
# 在Colab中安裝Prophet
!pip install prophet

from prophet import Prophet

(2) 數據準備

# 重新組織數據為Prophet需要的格式
df = close.reset_index()
df = df.rename(columns={'Date': 'ds', 'Adj Close': 'y'})

(3) 建立並訓練模型

# 建立模型
model = Prophet()

# 訓練模型
model.fit(df)

(4) 預測

# 創建未來日期數據框
future = model.make_future_dataframe(periods=30)

# 進行預測
forecast = model.predict(future)

# 查看預測結果
forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail()

(5) 可視化結果

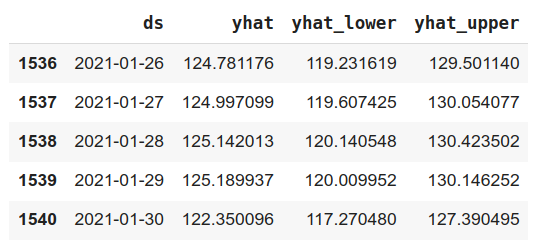
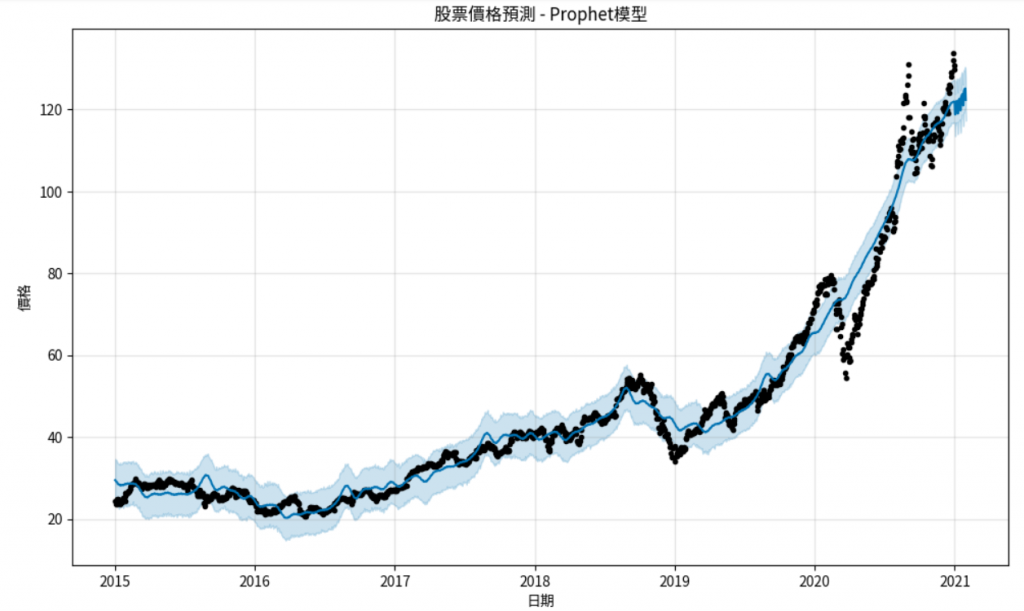
# 繪製預測結果
model.plot(forecast)
plt.title('股票價格預測 - Prophet模型')
plt.xlabel('日期')
plt.ylabel('價格')
plt.show()

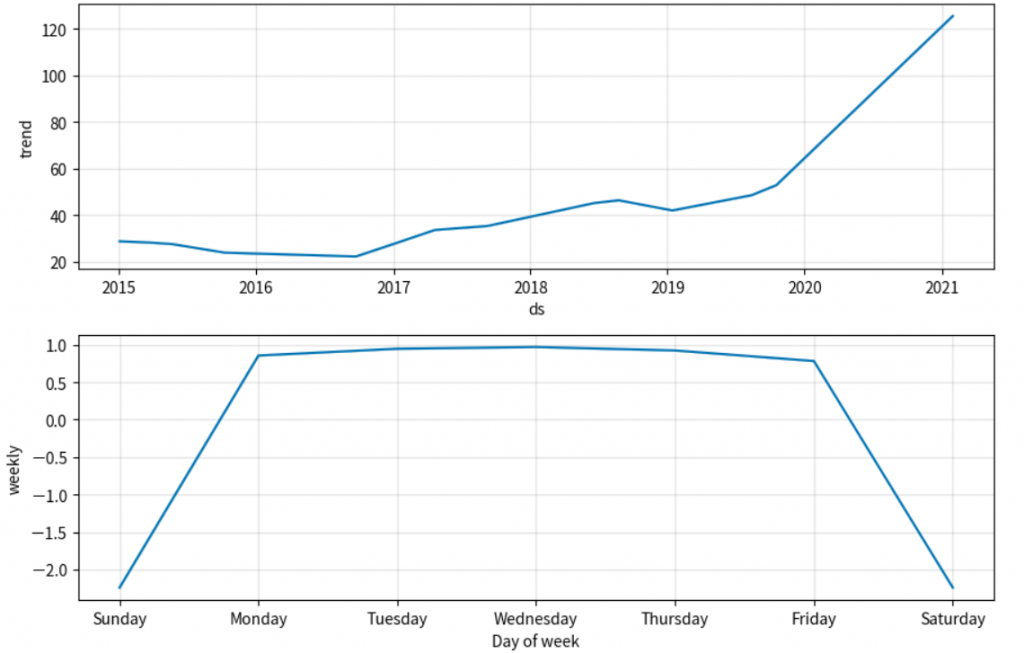
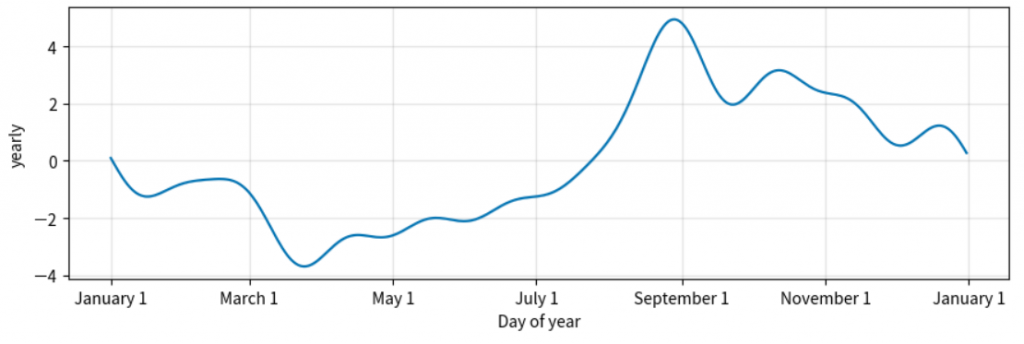
# 繪製組成成分圖
model.plot_components(forecast)
plt.show()

四、時間序列預測的關鍵概念

1. 自相關與偏自相關

• 自相關：序列與其滯後值之間的相關性，反映了時間序列的內在結構。

• 偏自相關：在給定中間滯後值的情況下，序列與其滯後值之間的相關性。

2. 差分與平穩性

• 差分：消除序列中的趨勢和季節性，使其平穩。

• 平穩性：平穩序列的統計特性（均值、方差、自相關）不隨時間變化，是時間序列建模的基本假設。

3. 模型評估與診斷

• AIC（Akaike Information Criterion）：用於模型選擇，AIC值越小，模型越好。

• 殘差分析：檢查模型的殘差是否為白噪聲，以驗證模型的適用性。

五、實際案例：比較ARIMA與Prophet模型

1. 模型性能比較

• 評估指標：均方誤差（MSE）、均方根誤差（RMSE）、平均絕對百分比誤差（MAPE）等。

from sklearn.metrics import mean_squared_error, mean_absolute_error

# 提取實際值和預測值
actual = df['y']
arima_pred = model_fit.predict()  # ARIMA模型的預測
prophet_pred = forecast['yhat']  # Prophet模型的預測

# 計算RMSE
rmse_arima = np.sqrt(mean_squared_error(actual, arima_pred))
rmse_prophet = np.sqrt(mean_squared_error(actual, prophet_pred[:len(actual)]))

print(f'ARIMA模型的RMSE: {rmse_arima:.2f}')
print(f'Prophet模型的RMSE: {rmse_prophet:.2f}')

2. 結果分析

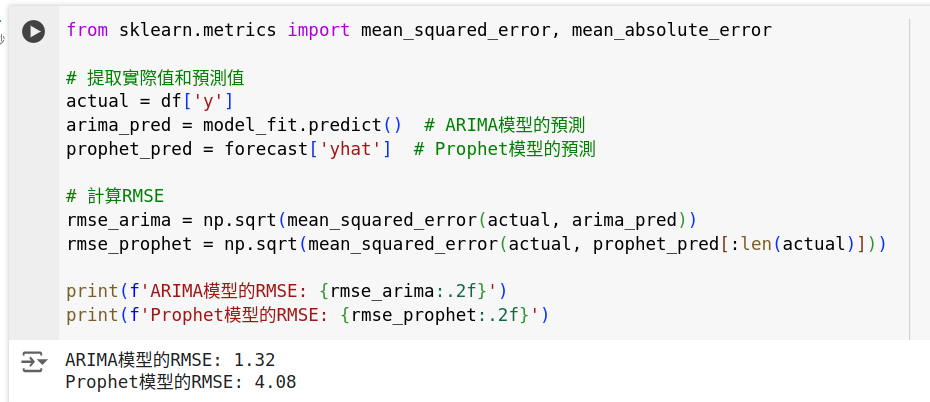
• 選擇模型：根據評估指標選擇表現較好的模型。

• 適用性：ARIMA適合於平穩的時間序列，而Prophet對於具有明顯趨勢和季節性的數據更有效。

六、總結

在本節中，我們：

• 了解了時間序列分析的基本概念，如自相關、差分和平穩性，為時間序列建模奠定了理論基礎。

• 學習了ARIMA模型的構建與應用，包括模型參數的確定和模型診斷。

• 掌握了使用Prophet模型進行預測，並理解了其優勢和適用場景。

• 比較了兩種模型的性能，了解了如何根據數據特性選擇合適的模型。

時間序列預測在金融分析中具有廣泛的應用，熟練掌握這些模型將有助於提高預測的準確性和可靠性。

作業：

1. 應用ARIMA模型：選擇一支股票或其他時間序列數據，進行差分處理，建立ARIMA模型，並進行未來30天的預測。

2. 應用Prophet模型：使用相同的數據，建立Prophet模型，進行預測，並比較兩種模型的結果。

3. 模型優化：嘗試調整ARIMA模型的參數（p, d, q）或Prophet模型的設定（如添加節假日效應），觀察對預測結果的影響。

透過實踐，您將更深入地理解時間序列預測模型的應用，並能夠在實際的金融分析中選擇合適的模型。

提示：

• 模型參數選擇：可以使用自動化的方法（如auto_arima）自動選擇最佳的ARIMA模型參數。

  !pip install pmdarima
  from pmdarima import auto_arima
  
  auto_model = auto_arima(close, seasonal=False, trace=True)
  print(auto_model.summary())
  

• 處理季節性：如果數據存在季節性，可以使用SARIMA或在Prophet中指定季節性參數。

• 模型診斷：在模型訓練後，務必進行殘差分析，確保模型的殘差滿足白噪聲的假設。

注意：

• 數據質量：確保數據的完整性和準確性，避免缺失值和異常值對模型造成影響。

• 預測不確定性：金融市場具有高度的不確定性，模型預測僅供參考，不能完全依賴。

• 避免過擬合：在模型構建時，避免使用過多的參數，導致模型過擬合歷史數據而無法泛化。