昨天講了Math.ceil()，數學中是「上取整函數」；今天要介紹的Math.floor在數學中也有對應的函數「下取整函數」，因為跟昨天的內容很相似，所以會互相比對一下差異，一起來看看吧！

「寐偲，伏漏兒！！」

數學課

數學中的下取整函數floor(x)從字面上也很好理解，就是「地板」的概念，取得了比自己本身小的整數值，一樣來看看他的函數圖形吧！

p(x) = floor(x)：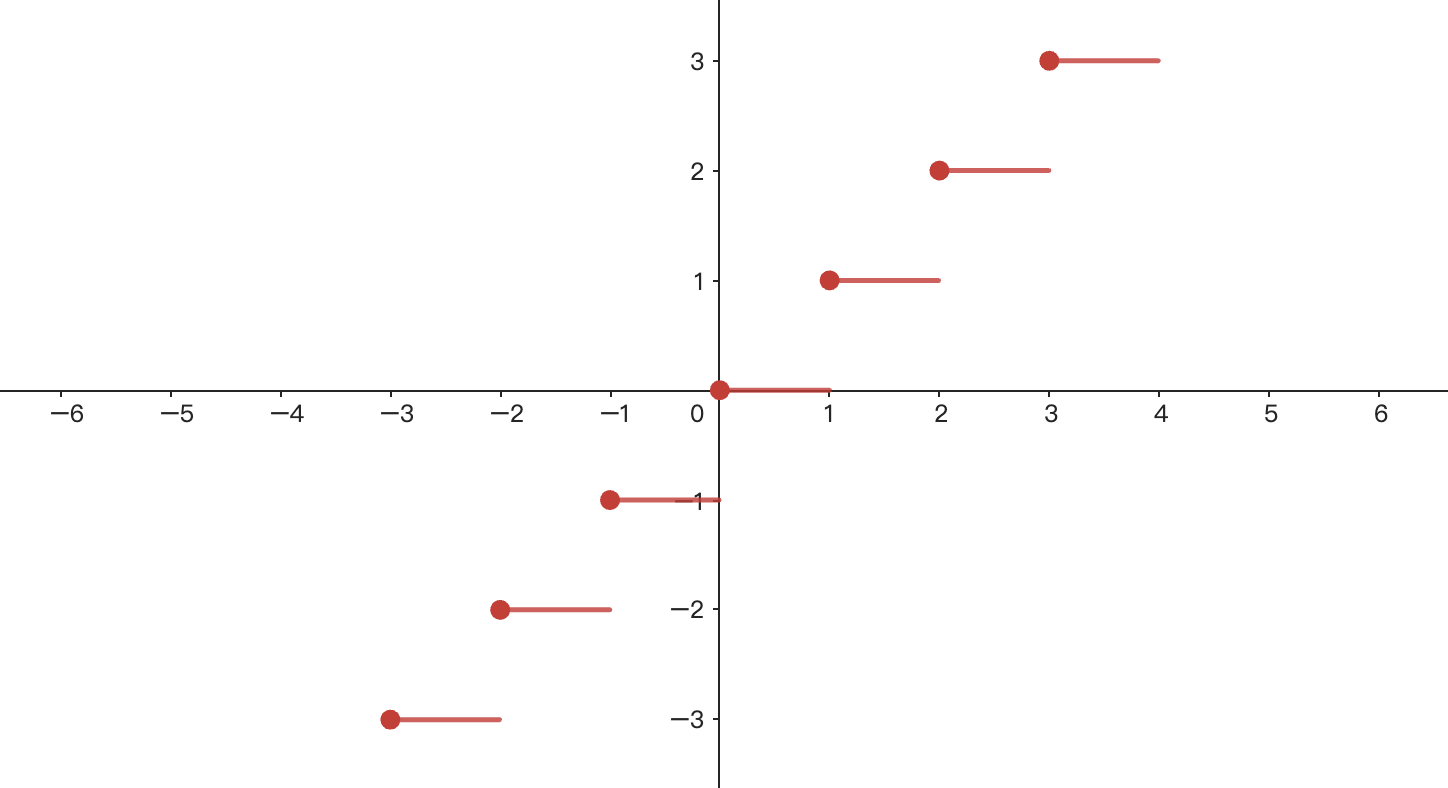

熟悉的階梯圖形～但跟p'(x) = ceil(x)不一樣的地方就在於每個線段的最左及最右側點，p(x) = floor(x)的線段最左側是實心（包含），最右側是空心的（不包含），跟p'(x) = ceil(x)是相反的。舉例來說就是floor(1)回傳1，比1小一點的數代進去：floor(0.999999)就會回傳0，一樣有疑惑可以去搜尋「下取整函數」。

進入重頭戲Math.floor()！！

Math.floor()

有了數學的下取整函數，Math.floor()就很好理解了！來看看如何使用吧！

語法

Math.floor(x)

參數

傳入一個數字

回傳值

它會回傳小於或等於x的最大整數。值會跟-Math.ceil(-x)的值一樣。

規範

這個函式會回傳不大於x的最大整數。
如果x已經是整數，那就回傳x。

有了昨天的經驗，那個greatest(closest to +∞)應該就不是問題了吧！

我的裡解就是他先向下取了比x小的整數，再從中往+∞方向取最大的整數。

一樣如果有不同看法歡迎留言討論！

最後來用用看就輕鬆結束這一天吧～

console.log(Math.floor(0.00003)); //0
console.log(Math.floor(-0.003)); //-1
console.log(Math.floor(4.7)); //4
console.log(Math.floor(-4.7)); //-5

與Math.ceil()的差異

• Math.ceil(x)：是天花板！所以是「往上」取最小整數，可以理解成無條件進位，不管正數負數，保持「往正」的方向取整數。
  • Math.ceil(4.7)回傳5。
  • Math.ceil(-4.7)回傳-4。
• Math.floor(x)：是地板！所以是「往下」取最大整數，可以理解成無條件捨去，不管正數負數，保持「往負」的方向取整數。
  • Math.floor(4.7)回傳4。
  • Math.floor(-4.7)回傳-5。

參考資料：
維基百科-取整函數
MDN-Math.floor()
ECMAScript-Math.floor()