使用 Merkle 樹在簽章系統中的主要好處是：有效管理多個密鑰對、減少公開金鑰的數量、提高簽名驗證的效率、增強安全性和靈活性，同時提供了防篡改的保證。這使得 Merkle 樹非常適合於在需要大量單次簽名的系統中應用。

Merkle Tree （雜湊樹）的結構

雜湊樹是一個二元樹，意思是形如以下的樹狀結構

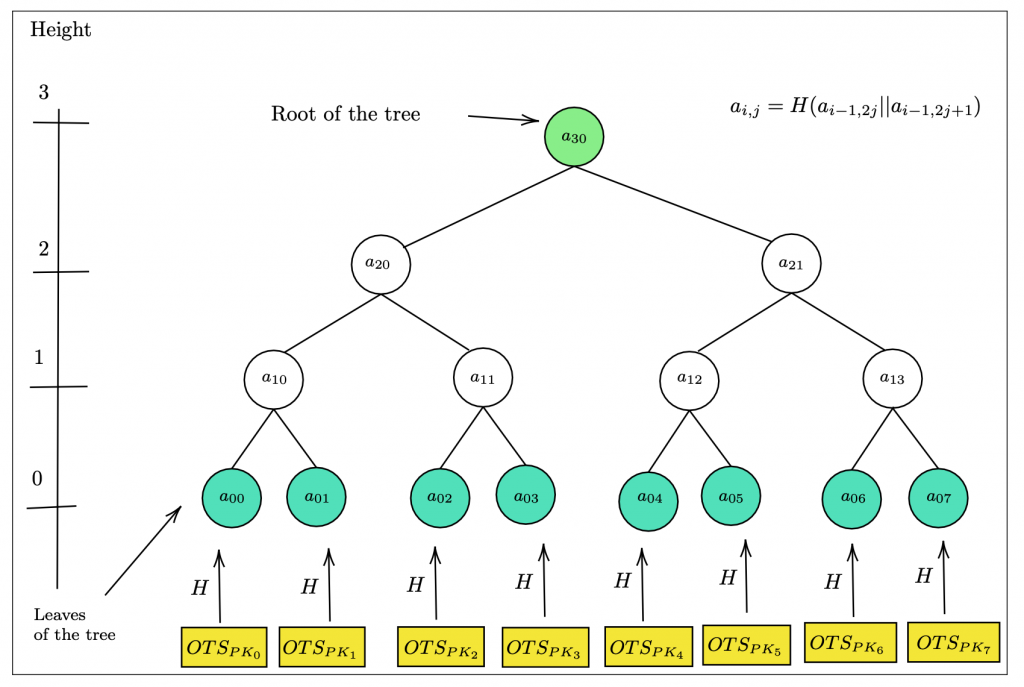
其中

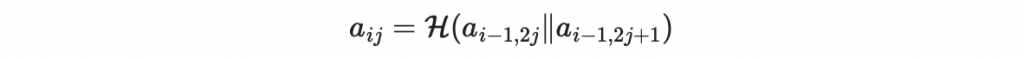
看起來有點複雜。所以我們舉例來說：

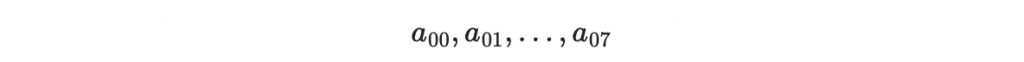
都是給定的字串，在今天的討論裡這些字串會是某八次的一次性簽章的公鑰（等等會細講）。接著

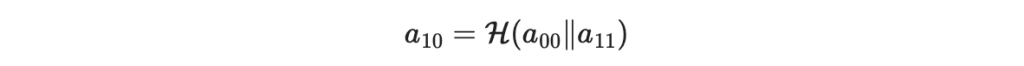
意思是 a_10 是由 a_00 嫁接 a_11 後代入 hash 函數的結果。你可以從圖片上看到，這個操作就是 a_10 他低一層的兩個字串嫁接後代入 hash 的結果。

以此類推來生成所有的樹狀節點，再舉一例：第二層第一個字串為

如何幫助簽章

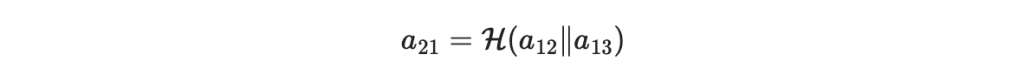
開頭提到：「有效管理多個密鑰對」、「減少公開金鑰的數量」。

我們結合 Merkle tree 與 WOTS+ 來進行實例說明：

原先的系統

• 鑰匙生成：
  • 選擇 w 為系統參數，我們會把要簽章的對象以每 log2(w) 位元為一區塊逐區塊進行簽章
  • 生成私鑰為 n 位元二進位字串，生成 r 為 w-1 個 n 位元二進位字串。

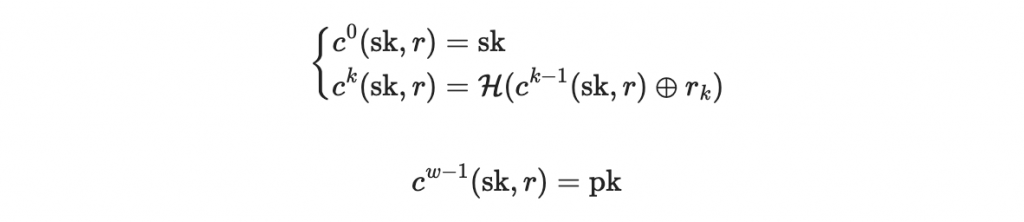
並發布所有公鑰

• 簽章過程

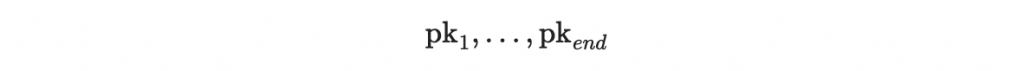
根據區塊值 M_i 生成

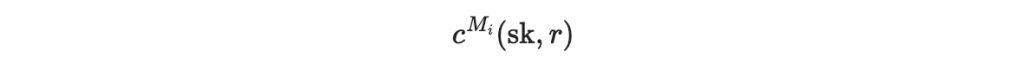
發布此區塊簽章為

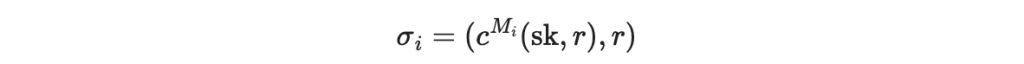
整個文件的簽章為

• 驗章過程
  對每個區段的簽章逐一進行驗章

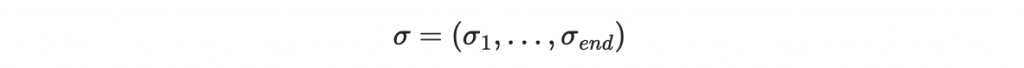
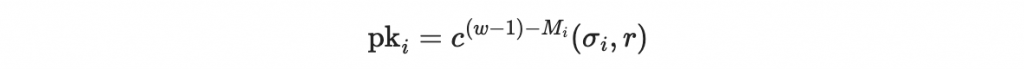
你可以注意到，驗證方必須在一開始保存一堆公鑰，事後一塊一塊進行驗章，若使用 Merkle tree 的不可篡改性，這個儲存公鑰的步驟可以簡化。

使用 Merkle tree 改進的系統

鑰匙生成一樣照做。生成每個區段的公鑰後

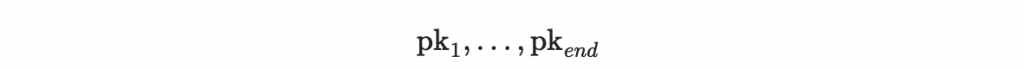
使用一個足夠大小的 Merkle tree 將這些公鑰作為節點，找出 Merkle tree 的最上層（Merkle tree root）將其發布為公鑰

如果 WOTS+ 公鑰數量不恰好是 2 的倍數，那你可以把剩下的節點隨機生成更多公鑰或者更多隨機字串。

簽章步驟照做，但最後要發布出去：

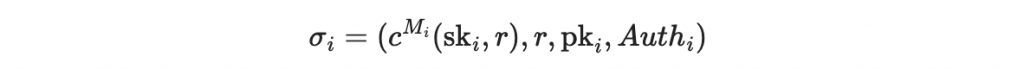
最後的 Auth 我們驗章時解釋。

你可能會問說，那這不是還是要把每個區段的公鑰都發出去嗎？有什麼改進？

答案是，對，這個公鑰還是得發，但是這是在上面那個 Merkle root 總公鑰發不完了之後才發出的區段公鑰，意思是說，「因為一開始沒有把區段公鑰給發出去，所以好像區段公鑰是可以偽造的（也就是簽章的時候順便做出來反正沒人知道），但是因為總公鑰 Merkle root 的存在，所以這個區段公鑰不能被更動，簽章者（攻擊者）不能偽造簽章」

驗章步驟就變成有兩步驟：

1. 檢查

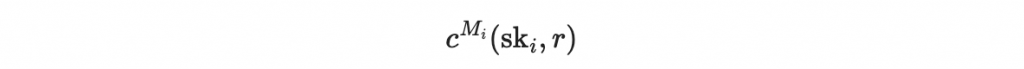
確實為區段公鑰 pk_i 的簽章
2. 檢查區段公鑰 pk_i 確實是 Merkle tree 的一部分。剛剛簽章一併發出來的

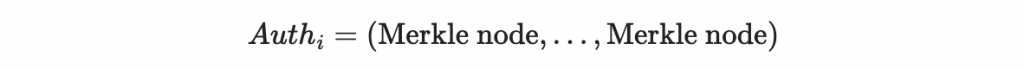
是從 pk_i 到 Merkle root 總公鑰途中所有需要的 Merkle 節點，為了讓驗章者可以算上去確認總公鑰，我們需要提供這個路徑與節點給他。

ref:

SRIVASTAVA, Vikas; BAKSI, Anubhab; DEBNATH, Sumit Kumar. An overview of hash based signatures. Cryptology ePrint Archive, 2023.