2024 iThome 鐵人賽

DAY 19

Security

「後量子密碼學」- 未來資訊安全的基礎系列第 19 篇

Day19 WOTS+ 區塊化的一次性簽章

16th鐵人賽

cesare381

2024-09-30 23:51:39

70 瀏覽

分享至

我們昨天介紹了 LD-OTS 簽章，這個系統是對訊息的每個位元逐一進行簽章，也因此最後的簽章大小非常大。今天來修改一下做法，我們對訊息字串的四個四個，或八個八個一塊一塊進行簽章，這也許可以大大降低最後的簽章大小。

概念介紹

假設我們要簽章的訊息為

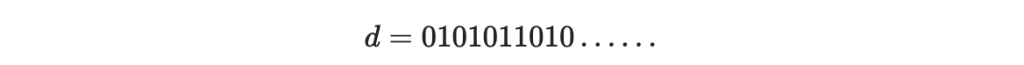
那其實可以不用逐個位元進行簽章，而是一段一段進行簽章，我們這裡一次對四個位元進行簽章。

其中最尾端的部分如果有缺項就補零進去。

每個區塊都可以計算其區塊值，就是他這個區塊所表達的二進位數值

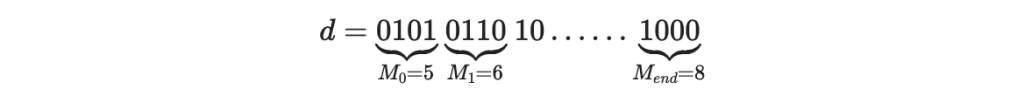
現在我們將對每個區塊進行簽章，過程中會用到
私鑰：首先會對這個區塊生成一把私鑰 sk ，基本上可當作一個 n 位元的隨機二進位字串。

公鑰：
一個 hash 函數 H
生成 15 個 n 位元的隨機二維字串 r = r_1, r_2, ..., r_15。
驗證用的鑰匙 pk 會用以下的方式來計算：

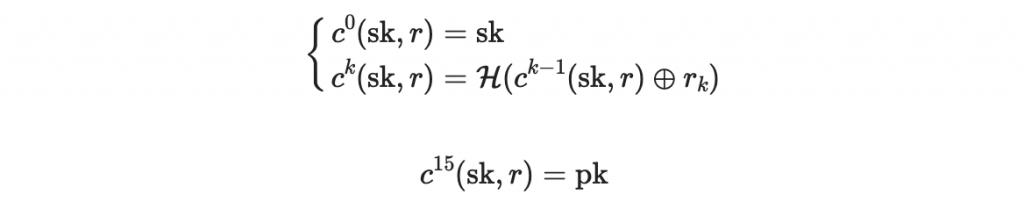
（你很快會看到為什麼這裡是十五）

以第一個區塊 0101 為例，其區塊值為 M0。此區塊的簽章會根據以下方程決定

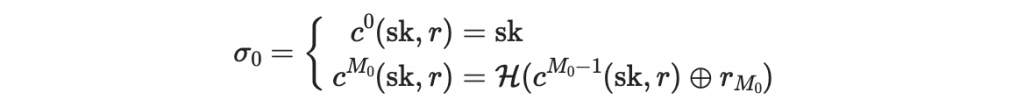
在這個例子裡， M0 = 5，所以

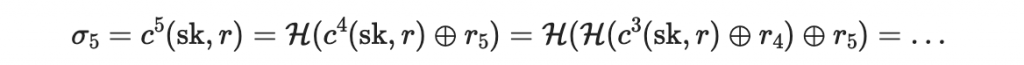
以此類推，就可以對每一個區塊進行簽章（請注意每個區塊都共用一樣的 r 字串、另外也請注意 M0 的最大值為 15 因此 r 字串只需準備十五個）

至於驗證的部分，驗證者拿到

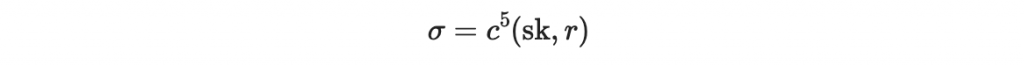
以及公鑰裡面的 r 、文件的區塊值 M0，就可以繼續做出

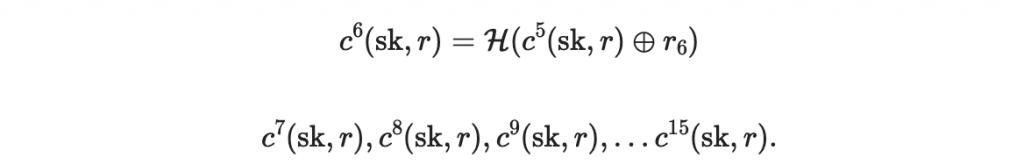
（因為知道文件的區塊值，所以同樣計算 c 的規則再做 15 - M0 次即可得到 c^15(x,r) 。）
而上面最後一個數值就恰好是我們之前設定的驗證用鑰匙 pk

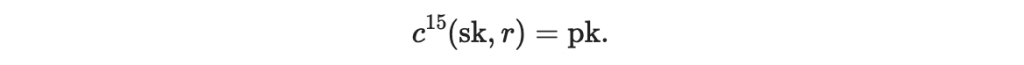
若這個等式成立，則這個區塊的簽章為有效。

將同樣的流程重複於文件的每一區塊，最後就可以得到所有的簽章，在對每一區塊進行同樣的驗章流程，即可確認簽章是否有效。

但是有一個小問題

通常一個有數字的文件很可能是重要的敏感資訊，這類文件也通常要使用簽章系統來保護。

假設有一個要簽章的文件，裡面包含數字 1000，而且很不幸的，這個 1000 就剛好完美地落在一個區塊裡面：

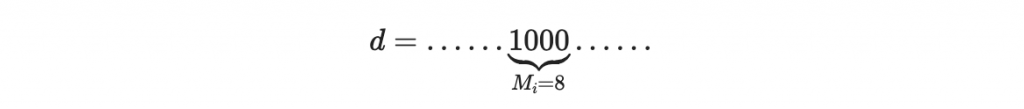
那麼根據簽章流程，這個區塊的簽章為

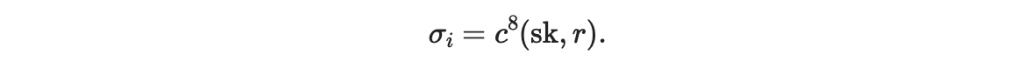
正常的簽驗章流程都能如預期進行。

但是如果今天有不肖人士（攻擊者）想要把文件裡面的 1000 改成 1001，那麼他完全可以計算

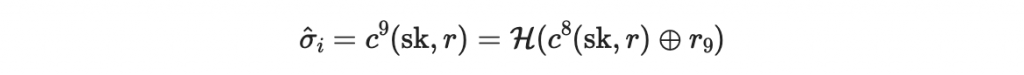
因為 r_9 是公鑰的一部分， H 也是公鑰的一部分。攻擊者計算完畢後，可以把原本的簽章

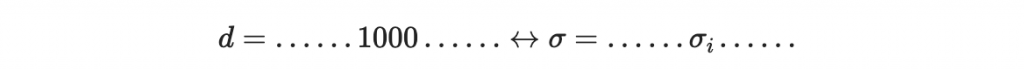
替換為

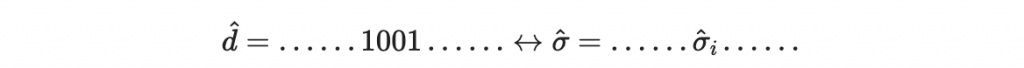
於是，偽造的簽章就流出在網路上了，而且根據簽章的特性，原本的簽章者不能否認攻擊者偽造的文件。

解決方法

這個攻擊之所以有效，是因為從 c^i 計算 c^(i+1) 是簡單的，但是反之，從 c^(i+1) 算回 c^i 是極其困難，因為當中涉及到要計算 hash 函數的反函數。（我們甚至可以說這個計算是不可能的，因為 hash 的不可逆性是整個 hash-based cryptography 的最基礎的假設。）

借用「錯誤更正碼」的想法：假設我們可以在文件 d 的後面，加上一些「冗余」（redundancy），好滿足說「當前面文件裡的某個區塊值增加的時候，後面『冗余』的某區塊其區塊值會減少」。

如此一來，同樣的攻擊，雖然確實可以在前面文件裡某個區塊值增加的時候簽出一個正確簽章，但是卻沒辦法在後面冗余部分，區塊值減少的地方簽出正確的簽章。這裡再重複一次：「從 c^(i+1) 算回 c^i 是極其困難，因為當中涉及到要計算 hash 函數的反函數」

那麼具體的設計該怎麼做呢？我們可以設計一個英文叫 checksum 的冗余在後面，我將中文翻譯為「數值和檢查碼」（基本上就是直翻😂）

我們令「數值和檢查值」為

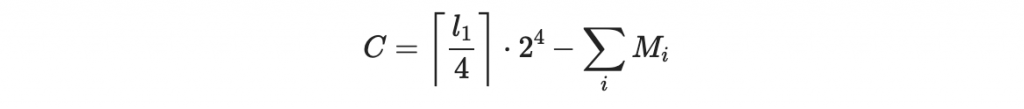
其中 l_1 為文件 d 的二進位長度。這個 C 永遠是正數，因為每個 M_i 都不超過 15 ，而且 M_i 的個數不超過 l_1 除以 4 的天花板函數。你馬上注意到當某個區塊值 M_i 增加時，這個數值和檢查值 C 是變小的。

接著我們講 C 寫成二進位，並嫁接在原本要簽章的 d 後面：

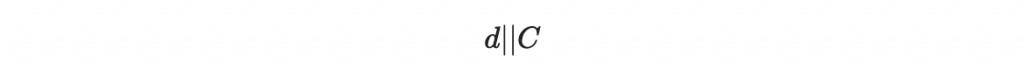
然後根據我們上面第一章的做法，對這個 d 與 C 的大字串進行逐區塊的簽章。於是，我們就成功防禦了本章一開頭所介紹的攻擊。

最後的一點功課

注意到 C 最大為

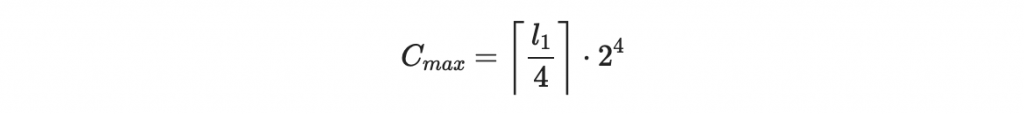
所以將他表為二進位字串時，最大長度為

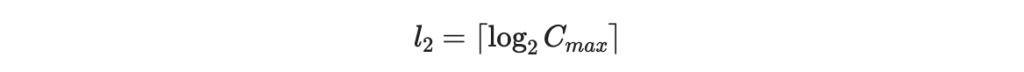
所以我們可以直接在原本的文件後面加上 l_2 個位元，缺項直接補零。

完整系統

好！到目前為止我們都使用 4 為一個區塊的大小，實際上這個數字是可以更改的，並且是公鑰的一部分。

鑰匙生成

決定區塊大小，一個區塊由

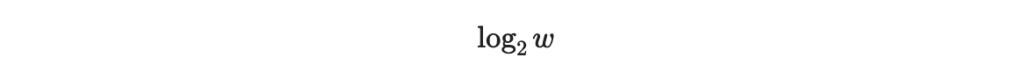
個位元組成，其中 w 為二的某次方。（上面的舉例中 w = 16, log_2(w) = 4）

數值和檢查值最高為

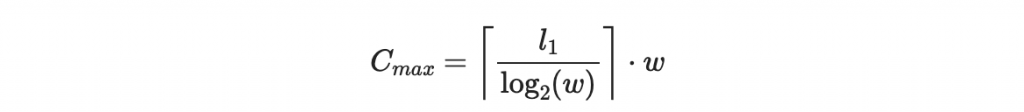
其中 l_1 為本來要簽章的文件 d 的二進位字串長度。所以我們將會在 d 後面增加

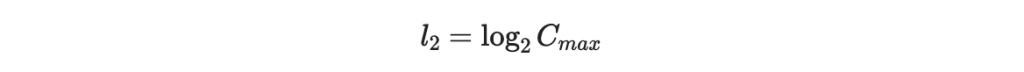
位元的數值和檢查碼。全長為

每個區段為 log_2(w) 位元，所以我們最多需要

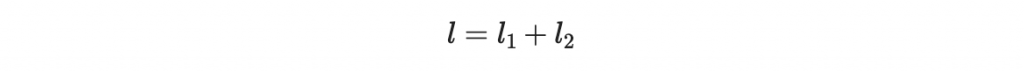
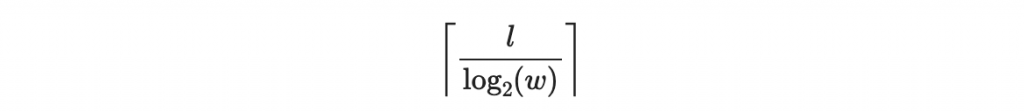
個私鑰 sk ，這個私鑰本質上就是一個 n 長度的隨機二進位字串。
4. 公鑰另外還包含 w-1 個長度 n 的隨機二進位字串 r = r_1, r_2, ...
5. 驗證用的鑰匙 pk 會用以下的方式來計算：

簽章

將文件 d 分為長度為 log_2(w) 的區塊

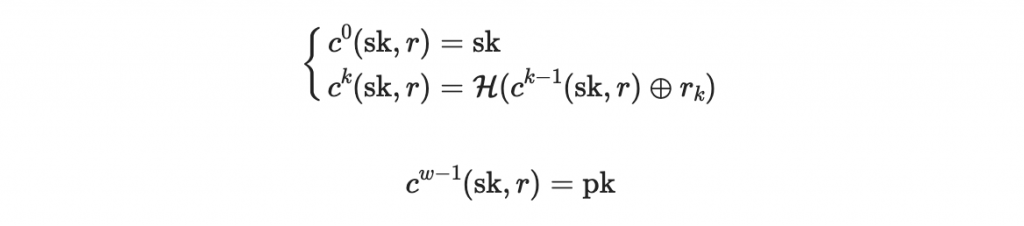
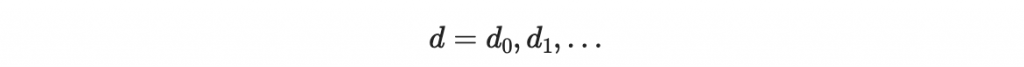
並計算每個區塊的區塊值 M_i 。
2. 計算數值和檢查值

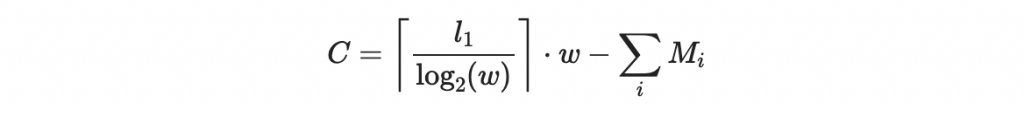
並以二進位表示法嫁接在文件 d 的後面。
3. 對於大字串

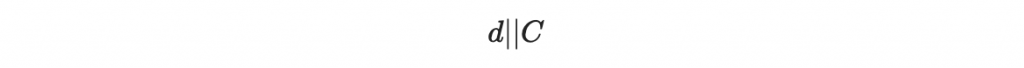
逐區段進行簽章。每個區塊根據其區塊值 M_i 生成簽章

發送簽章

驗章

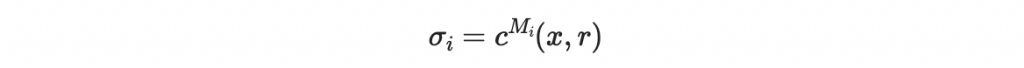
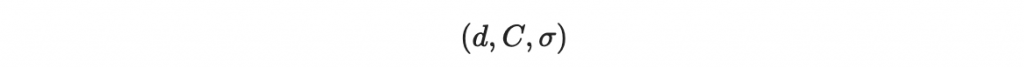
直接針對大字串

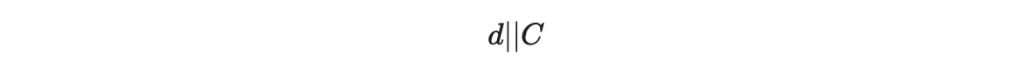
逐區段進行驗章即可。

進行實作

首先先設定 hashlib 以及要使用的 hash 函數

import hashlib
import random

# 定義哈希函數 (SHA-256)
def hash_func(data):
    # 計算 SHA-256 哈希值
    sha256_hash = hashlib.sha256(data.encode()).digest()
    
    # 將哈希結果轉換為二進制格式，並返回 256 位的二進制字串
    return ''.join(f'{byte:08b}' for byte in sha256_hash)

# 將訊息轉換為二進位字串
def message_to_binary(message):
    return ''.join(format(ord(c), '08b') for c in message)

訊息與參數選擇

# 訊息與參數選擇
message = "Hi! This is Cesare!"
binary_message = message_to_binary(message)
print(f"訊息的二進位表示: {binary_message}")
l1 = len(binary_message)
print("l1 = ", l1)

w = 256 
logw = 8 # 我們使用八個位元為一個區段

# Outputs:
# 訊息的二進位表示: 01001000011010010010000100100000010101000110100001101001011100110010000001101001011100110010000001000011011001010111001101100001011100100110010100100001
# l1 =  152

鑰匙生成

# 鑰匙生成

# 首先計算最大可能的數值和檢查和

C_max = ((l1//logw)+1)*w

# 最長可能的數值和檢查碼

l2 = len(bin(C_max))-2

print(f"最大可能的數值和檢查碼: {C_max} ({l2} bits)")

# Outputs:
# 最大可能的數值和檢查碼: 5120 (13 bits)

# 鑰匙生成
# 生成私鑰
l = l1 + l2
print(f"l1 = {l1}, l2 = {l2}, l = {l}")

# 計算最多需要幾把私鑰
num_of_sk = (l//logw)+1
print(f"需要的私鑰數量: {num_of_sk}")

# 生成私鑰
# 生成 n 位元的私鑰（256 位元）
def generate_n_bits_string(n=256):
    random.seed(42)  # 設定種子
    return ''.join([str(random.randint(0, 1)) for i in range(n)])

private_keys = [generate_n_bits_string() for i in range(num_of_sk)]
print(private_keys[0])

# Outputs:
# l1 = 152, l2 = 13, l = 165
# 需要的私鑰數量: 21
# 0010000010000000101100111001001011101010110000100011110110100001110100011100101110100111100100000101111001101101010010010011001100000100010110011111000010000000001001100101100011111000110000101011001000000111010010111111001000100100000001000011101011011100

# 鑰匙生成
# 計算公鑰

# XOR 兩個字串 
def xor_bits(a, b):
    result = ""
    for i in range(len(a)):
        result += str(int(a[i]) ^ int(b[i]))
    return result

def c_value_iterate(c_value_prev, r_to_be_xor):
    return hash_func(xor_bits(c_value_prev, r_to_be_xor))  # XOR 和哈希操作
    
def pk_gen(sk, r):
    result = sk
    for i in range(1,w):
        result = c_value_iterate(result, r[i])
    return result

# 生成公鑰裡面的 r  
r = [(generate_n_bits_string(n=256)) for _ in range(w)]
# 為了方便使用下標，我們多生了一個 r[0] 但我們不會用它
# 現在起 r1 = r[1], r2 = r[2], ..., r_{w-1} = r[w-1]




pk = [pk_gen(private_keys[0], r) for _ in range(w)]
print("The first public key is:\n"+str(pk[0]))

# Outputs
# The first public key is:
# 1010101101010110010000010000110101110000001011010101110100111010100010001101101111111011011000010100110101001001101001111101010011100110010110100110101101001010110101010001111001001000011110111010011001001101011110010110100001010110001111001001001010100111

簽章

# 簽章
# 計算數值和檢查值

print(binary_message)

segment = []
for i in range(0, len(binary_message), logw):
    segment.append(binary_message[i:i+logw])
    if len(segment[-1]) < logw:
        segment[-1] = segment[-1] + "0"*(logw-len(segment[-1]))
print(segment)

# 計算區塊值
segment_values = [int(s, 2) for s in segment]
print(segment_values)

C = ((l1//logw) + 1) * w - sum(segment_values)
print(f"數值和檢查值: {C}")
print(f"數值和檢查值的二進位表示: {bin(C)[2:]}")


# Outputs: 
# 01001000011010010010000100100000010101000110100001101001011100110010000001101001011100110010000001000011011001010111001101100001011100100110010100100001
# ['01001000', '01101001', '00100001', '00100000', '01010100', '01101000', '01101001', '01110011', '00100000', '01101001', '01110011', '00100000', '01000011', '01100101', '01110011', '01100001', '01110010', '01100101', '00100001']
# [72, 105, 33, 32, 84, 104, 105, 115, 32, 105, 115, 32, 67, 101, 115, 97, 114, 101, 33]
# 數值和檢查值: 3558
# 數值和檢查值的二進位表示: 110111100110

# d || C 大字串
dC = binary_message + bin(C)[2:]
print(f"d || C 大字串: {dC}")

segment = []
for i in range(0, len(dC), logw):
    segment.append(dC[i:i+logw])
    if len(segment[-1]) < logw:
        segment[-1] = segment[-1] + "0"*(logw-len(segment[-1]))
print(segment)
print(len(segment))


# Outputs:
# d || C 大字串: 01001000011010010010000100100000010101000110100001101001011100110010000001101001011100110010000001000011011001010111001101100001011100100110010100100001110111100110
#
# ['01001000', '01101001', '00100001', '00100000', '01010100', '01101000', '01101001', '01110011', '00100000', '01101001', '01110011', '00100000', '01000011', '01100101', '01110011', '01100001', '01110010', '01100101', '00100001', '11011110', '01100000']
#
# 21

# 簽章
signatures = []
for i in range(len(segment)):
    sg = segment[i]
    signature = private_keys[i]
    sg_value  = int(sg, 2)
    for j in range(1, sg_value+1):
        signature = c_value_iterate(signature, r[j])

    signatures.append(signature)

print(signatures[0])
print(len(signatures))


# Outputs:
# 1000100011111011010000001001111110110011000001001100010010110000100110001010111110001111001100110001110000101110010111011001011000111111101101101100101100001100101000101010110011111001011100110111000110101101101000101100011111100100001011111110111011000011
# 21

驗章

# 驗章
valid = 1
for i in range(len(segment)):
    sg = segment[i]
    signature = signatures[i]
    sg_value  = int(sg, 2)

    for j in range(sg_value+1, w):
        signature = c_value_iterate(signature, r[j])
    
    valid = valid and (signature == pk[i])
print(valid)

# Outputs:
# Ture

Takeaway

簽章區塊化以減少大小：透過將訊息分為多個位元區塊並逐區塊進行簽章，可以大幅減少簽章的大小，提升整體系統的效率。這樣的區塊化策略在現實中具備重要意義，特別是對於長度較長的訊息。
使用數值和檢查碼來增強安全性：加入「數值和檢查碼」（checksum）作為冗餘，可以有效防止攻擊者在某些區塊中篡改訊息。這個方法透過建立前後區塊間的依賴性，使篡改單一區塊變得困難。

ref
HÜLSING, Andreas. W-OTS+–shorter signatures for hash-based signature schemes. In: Progress in Cryptology–AFRICACRYPT 2013: 6th International Conference on Cryptology in Africa, Cairo, Egypt, June 22-24, 2013. Proceedings 6. Springer Berlin Heidelberg, 2013. p. 173-188.