今天來跟著助教和chatGPT了解一下菲涅耳光強方程式！ （今天來輕鬆一下！）

菲涅耳方程式（Fresnel Equations）是用來描述當光線從一個介質傳播到另一個介質時，在兩個介質交界面上發生的反射和折射現象。
這些方程式主要用來計算反射和折射光的振幅及強度，並取決於入射光的偏振方向。
這些現象遵循斯涅耳定律（Snell's Law），同時也受 Fresnel 方程式的描述。

Fresnel 方程式分為兩種情況：

1. 垂直偏振（S-偏振）： 電場振動方向垂直於入射面（即光線的入射平面）。在這種情況下，反射光和折射光的振幅與入射角和折射角有關，並由以下方程式給出：

   • 反射系數（反射振幅）：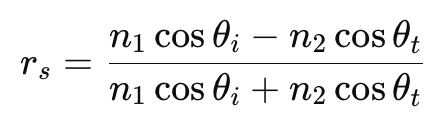

   • 折射系數（折射振幅）：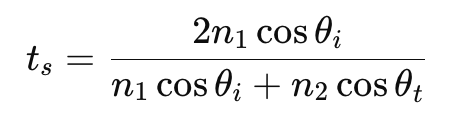

2. 平行偏振（P-偏振）： 電場振動方向平行於入射面。在這種情況下，反射和折射的振幅則由以下方程式描述：

   • 反射系數（反射振幅）：
   • 折射系數（折射振幅）：

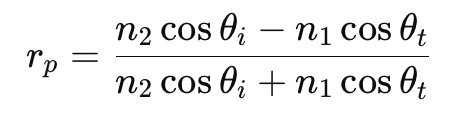
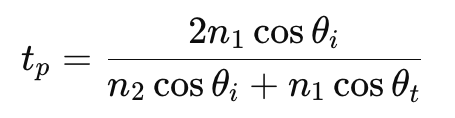
n1 和 n2 分別是兩個介質的折射率，θi 是入射角，θt 是折射角。

以下是將公式寫成程式：

import numpy as np
import matplotlib.pyplot as plt
from numpy import sin, pi, cos, arcsin
#因為後面會一直用不想重複寫np.故這邊先一次import


#定義介質折射率
n1 = 1
n2 = 1.5


#定義入射角，從0到pi/2之間切成200個等距點
theta_incident = np.linspace(0, pi/2, 200)
#定義折射角，依照snell定律利用反正弦得出角度
theta_transmit = arcsin((n1/n2)*sin(theta_incident))

#垂直偏振光的反射系數
r_TE = (n1*cos(theta_incident)-n2*cos(theta_transmit))/(n1*cos(theta_incident)+n2*cos(theta_transmit)) #穿透係數垂直偏振
#平行偏振光的反射系數
r_TM = (n2*cos(theta_incident)-n1*cos(theta_transmit))/(n2*cos(theta_incident)+n1*cos(theta_transmit)) #反射係數垂直偏振

#垂直偏振光的折射系數
t_TE = 2*n1*cos(theta_incident)/(n1*cos(theta_incident)+n2*cos(theta_transmit)) #垂直偏振
#平行偏振光的折射系數
t_TM = 2*n1*cos(theta_incident)/(n2*cos(theta_incident)+n1*cos(theta_transmit)) #垂直偏振

#繪製圖表，乘以180/pi是將入射角從弧度轉換為度數，alpha調整顏色透明度，--為虛線
plt.plot(theta_incident*180/pi, r_TE, 'b', label = 'r_TE')
plt.plot(theta_incident*180/pi, r_TM, 'r', label = 'r_TM')
plt.plot(theta_incident*180/pi, t_TE, 'b--', label = 't_TE', alpha = 0.5)
plt.plot(theta_incident*180/pi, t_TM, 'r--', label = 't_TM', alpha = 0.5)

#則在 y=0 的位置畫了一條水平線
plt.axhline (y=0,color='r', linestyle=' ', linewidth=1)

plt.xlabel('incident degree')
plt.legend()
plt.show()

畫出來圖表如下：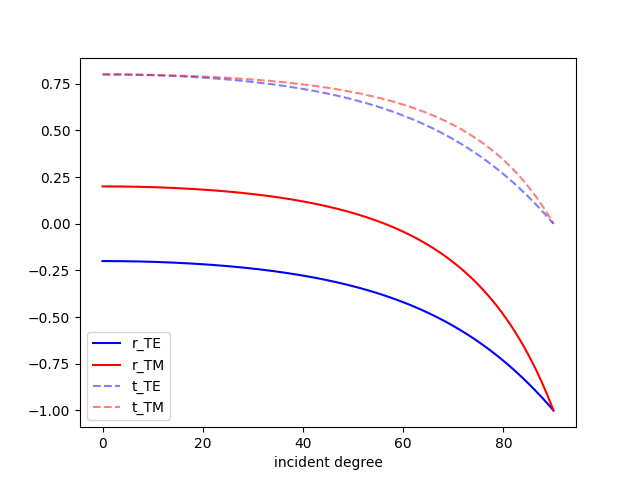

這樣就可以看到不同偏振方向和角度所對應的折射/反射率。

我們來接著畫這個：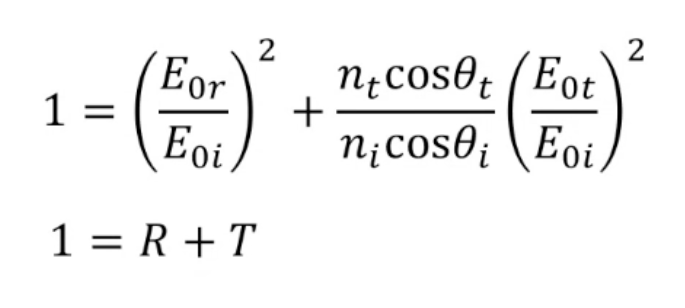

這個公式其實是與菲涅耳定律相關的光學現象中的能量守恆表達式。光波從一種介質入射到另一種介質時，反射率 R 和透射率 T 的和為 1。
公式中的 E0i E0r 和 E0i E0t 是反射和透射波的電場幅值相對於入射波電場幅值的比值。這些比值的平方分別表示反射率和透射率。

程式碼如下：

import numpy as np
import matplotlib.pyplot as plt
from numpy import sin, pi, cos, arcsin
#因為後面會一直用不想重複寫np.故這邊先一次import

#入射係數
n1 = 1

#出射係數
n2 = 1.5

#定義入射角，從0到pi/2之間切成200個等距點
theta_incident = np.linspace(0, pi/2, 200)
#定義折射角，依照snell定律利用反正弦得出角度
theta_transmit = arcsin((n1/n2)*sin(theta_incident))


#垂直偏振光的反射系數
r_TE = (n1*cos(theta_incident)-n2*cos(theta_transmit))/(n1*cos(theta_incident)+n2*cos(theta_transmit)) 

#垂直偏振光的折射系數
t_TE = 2*n1*cos(theta_incident)/(n1*cos(theta_incident)+n2*cos(theta_transmit)) 

#反射率
R = (r_TE)**2
#透射率
T = ((n2*cos(theta_transmit))/(n1*cos(theta_incident)))*t_TE**2

#製圖
plt.plot(theta_incident*180/pi, R, 'cadetblue', label = 'Reflection')
plt.plot(theta_incident*180/pi, T, 'salmon', label = 'Transmission')
plt.xlim(0,90)
plt.ylim(0,1)
plt.legend()
plt.show()

畫出圖如下：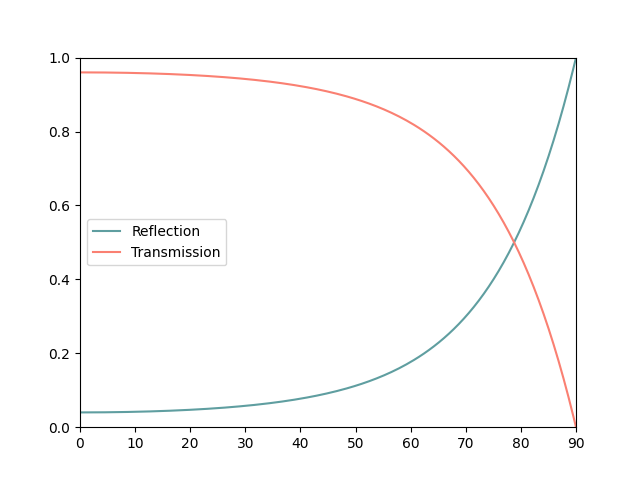

可以看到反射和折射和為1以及兩者的關係～代表著能量守恆！