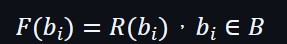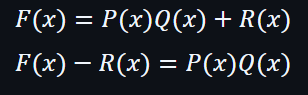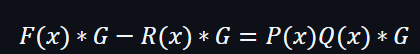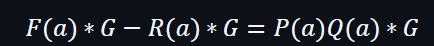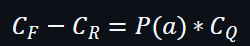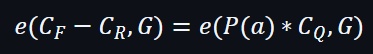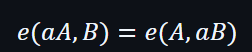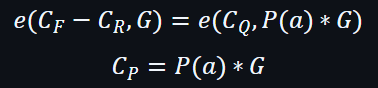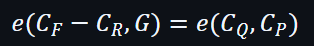不對稱配對

在多項式承諾中，除了會用到對稱配對，其實還有不對稱配對來進行正確性的證明。
在真實應用當中，不對稱配對也是常見的，與對稱配對的證明方式是相近的。
用以下例子加以說明一下: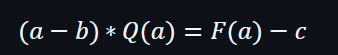

然後在公式的兩邊都加上G1: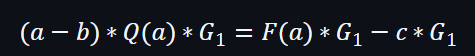

再簡化轉換: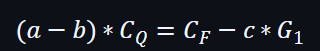

運用配對下: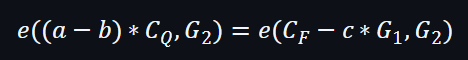

運用雙線屬性下: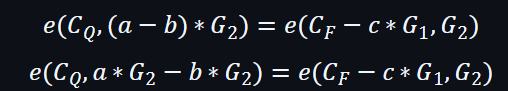

其實除了a值，G2也能在G1的SRS中被計算或者找到的。由於G2能被找到出來，所以在G2的SRS可以找到(a * G2)的值。
換言之，以上公式也是具可驗證的。

批量模式

批量模式 - 單個多項式和多個點

KZG 承諾還可以使用單一證明在多個點進行打開和驗證。
在一個獨立的打開，證明者可以評估 F(x) 在 b 上的值，從而計算 F(b) = c ，以及向驗證者提供證明 c 。
在一個批量模式，驗證者可以向證明者發出一組B: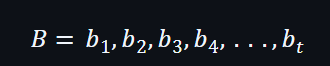

而證明者可以評估: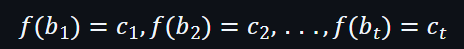

因此，可以建立出 C :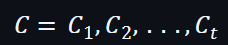

所以就可以有以下公式: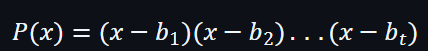

由於F(x)的degre是 d ，和存在一個條件是 t < d ，因此F(x)可以被P(x)整除的。
假設除法的商數為 Q(x) 而餘數為 R(x)。公式如下:
F(x) = P(x)Q(x) + R(x)

證明者會計算出Q(x)的值，及Q(x)的證明CQ，另外，也會向驗證者發出 C 集合。
證明者同時也可以發送 R(x) 給驗證者。另一方面，驗證者也可以自行通過以下方式找到多項式 R(x):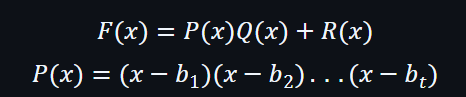

另外: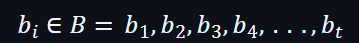

所以明顯地留意到，當P(x)為0時: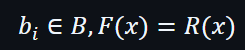

由於:

同樣地:

由於Q(x)的 degree 是 t ， 而R(x) 是 F(x)除以Q(x)的餘數，R(x) 的 degree 會必然小於 t 。
作為驗證者，是能夠知道R(x)在t點的值，所以可以通過Lagrange’s Interpolation找到R(x)，換言之，驗證者是會知道R(x)的。
驗證者也可以知道多項式P(x):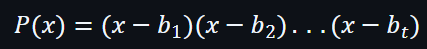

所以驗證者可以計算出 P(x) 和 R(x) 的承諾。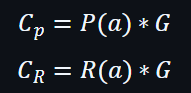

針對批量評估，驗證者可以根據以下步驟完成:

1. 驗證者可以檢查
   
   證明者會提供針對F(x)的評估 - C集合。
   再加上驗證者是知道 R(x)，所以只要集合上述的資料，就可以進行驗證。
2. 驗證者必須驗證以下等式是否成立
   
   在兩邊同時乘以產生器G
   
   評估在a點上的值:
   
   F(a) * G 、 R(a) * G 及 Q(a) * G 都是屬於G的元素，可以組成承諾，所以公式可以變成以下形式:
   
   去到這一步，驗證者是不知道a值，所以也沒辦法去計算到P(a)，不過驗證者可以運用配對方式。
   正如剛才提到F(a) * G 、 R(a) * G 及 Q(a) * G 都是屬於G的元素，因此所有由它們組成的承諾都是屬於G的元素，
   P(a)是一個標量，所以一個承諾乘以一個標量的值也是屬於G的元素。換言之，可以利用配對圖輔助證明:
   
   基於配對圖中的雙線屬性及P(a)是標量的條件下會有以下等式:
   
   將公式再進行轉換:
   
   因此:
   
   所以驗證者可以基於以上等式來進行驗證。