部分打開(Partial Open or Evaluation Proof)

在KZG中，證明者還可以進行部分打開(即是只進行單一值的評估)，這個也稱為評估證明。
在這裡會用其他例子說明，也希望讓大家可以更易理解學習。

驗證者可以由有限域Fp中隨機選一個b值發送到證明者，證明者會評估多項式 F(x) 在 x = b 時作為 F(b) = c 及發送
一個 c 到驗證者。證明者需要提供一個證明給驗證者 F(b) = c 。
而這個證明是由證明者向驗證者發出的一個商多項式證明 Q(x)。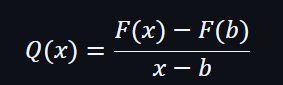

因此，假如F(x)是一個多項式，則F(x) - F(b) 是能夠被(x - b)整除的，餘數為0。
所以 Q(x) 是一個多項式，而它的分母中是沒有任何變數，同時也沒有任何負指數。
由於 Q(x) 是一個多項式，所以證明者可以計算出Q(x)的證明使用參考字串為: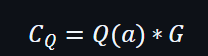

如果 F(x) 不能夠被(x -b)整除，就表示 Q(x) 存在一個變數分母或負指數，
而且證明者無法單單使用參考字串來評估它及不知道a值。

驗證部份

在承諾方案中所指的"完成"，是指所有真確的事，都能夠被證明的。
當所有真確的事能通過驗證，而且假的證明不能通過驗證之下，就表示這證明是足夠可靠的(soundness)

驗證者會有以下資料: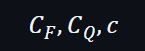

因此，驗證者可以進行驗證: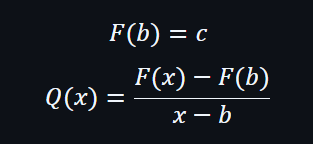

所以可以轉換為: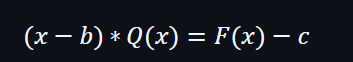

當評估 x = a 時: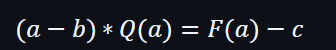

在公式中加上產生器G: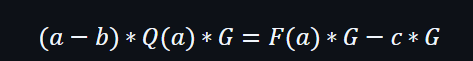

因此: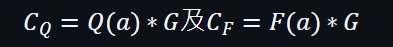

再通過轉換: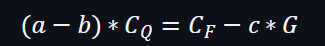

假如驗證者能夠驗證上述所有等式的成立，就表示驗證者已經驗證了承諾。由於驗證者不知道a值，所以驗證者都無法直接進行驗證，就需要通過其他資訊輔助完成驗證。
不過，驗證者可以利用橢圓曲線配對來進行驗證，在這情況之下，就算驗證者不知道a值，也是能夠直接去進行驗證。

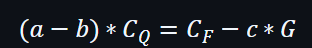
在上面的公式中，每一個輸入在配對圖中有需要是群內的元素，任何承諾都是該組生成器G的標量的倍數。
所以:

因此:

所以大家也可以看到，在公式上的所有輸入都是G的元素，也可以是配對圖中的輸入。
透過將等式的每一邊作為第一個參數，然後傳遞給映射和傳遞到 G 作為每一邊的第二個參數，可以將要驗證的相等性變成: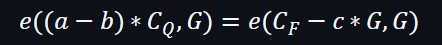

由於不知道a值，所以還需要其他輔助。不過配對圖中的雙線屬性可以表示: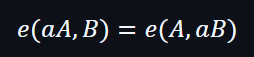

可以把公式修改為: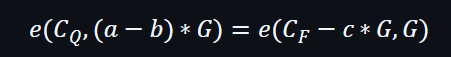

然後再進一步簡化: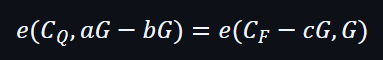

雖然仍然不知道a值，但是通過參考字串能知道G元素內的值，所以驗證者能夠完成到相關驗證。