為了介紹「編碼密碼學」，我們首先需要介紹「編碼理論」（Coding Theory）

編碼理論起源於訊息傳遞過程中遇到的「雜訊」問題。這些雜訊可能來自於不同來源，比如當我們將資訊透過電磁波從一個地點傳遞到另一個地點時，外太空的電磁干擾會影響訊號的完整性；又或者是當我們五年前將檔案存入電腦磁碟後，隨著時間經過，熱雜訊的累積導致資料出現損壞，今天提取該檔案時可能無法正確打開。這些現象都反映了在實際傳輸或儲存數據時，必須採用某些方法來抵禦這些錯誤。

為了解決這個問題，編碼理論提供了許多糾錯碼（error-correcting codes），能夠幫助檢測並修復錯誤。今天我們來詳細討論編碼理論裡面「線性編碼」（Linear Code）的概念。

線性編碼

首先訊息都是一串 0 和 1 組成的字串，例如：

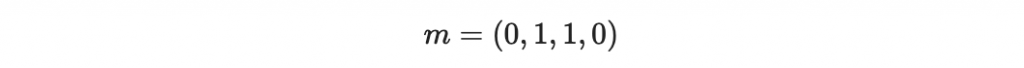
所以我們也可以把訊息當作一個「向量」來看待。

一種檢查錯誤的方式就是在訊息的後面增加一個「奇偶檢查碼」，例如上面的 m ，他的奇偶檢查碼就是

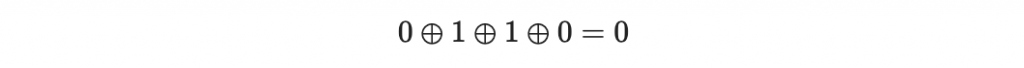
所以我們傳送 m 時就順帶將奇偶檢查碼 0 附加在後面一起傳送：

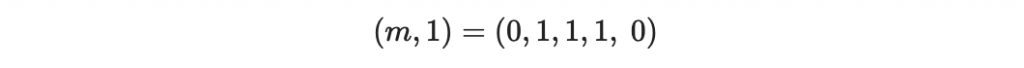
我們把這個組合的訊息叫做「碼字」（codeword）。

如果在過程中，有其中一個位元壞掉了（從零變成一或是從一變成零）：

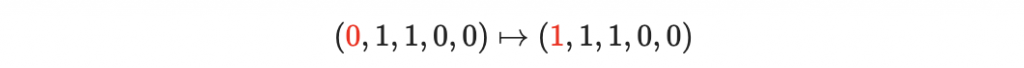
那麼接收者透過檢查奇偶檢查碼，發現

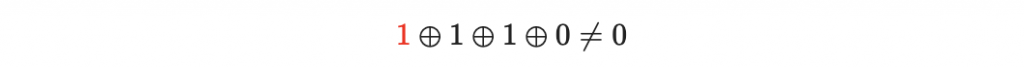
就可以馬上得知這個碼字，在傳遞的過稱中壞掉了。於是要求傳送者重新傳送一次。

聰明的讀者很快就注意到，如果碼字裡有兩處壞掉的話，那接收者是檢查不出來的。你的擔心一點也沒錯！所以以上的編碼方式並沒辦法完全依賴，我們需要尋找更多更好的編碼方式！接下來我們考慮另一種編碼方式：

一樣的訊息

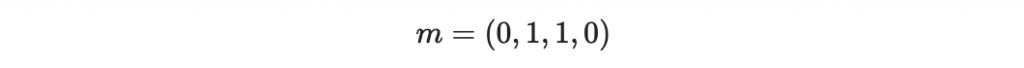
把每個位元都重複三次，形成以下的碼字

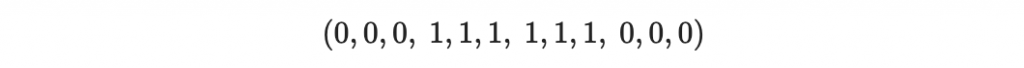
如果傳輸過程中兩個位元壞掉了，形成以下碼字

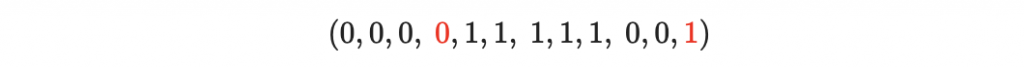
那接收者很快可以猜到訊息本身是

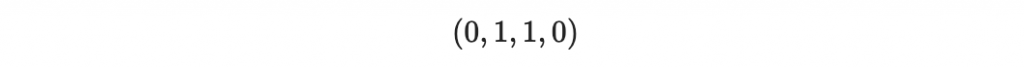
聰明的讀者很快就注意到，傳輸過程中也可以是以下兩個位元壞掉

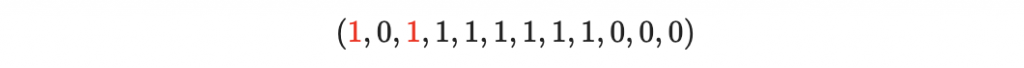
接收者就會誤會正確訊息是 (1,1,1,0) 。這表明，即使重複編碼也不是完美的解決方案。

（不過若從工程的角度考量，實際傳輸中同時出錯在一個區段的機率通常較低。因此，只要我重複的次數夠多次，我們可以將出錯的機率降到很低，但這會提升通訊成本。不過，這些工程問題並不是我們在「編碼密碼學」中關注的重點。詳情請洽關鍵字「編碼理論」以及最後的 ref）

生成矩陣

上面提到的編碼方式都可以使用一個「生成矩陣」 G 來描述。生成矩陣 G 是編碼過程中的核心工具，它將訊息向量轉換為碼字。

奇偶檢查碼

假設訊息為

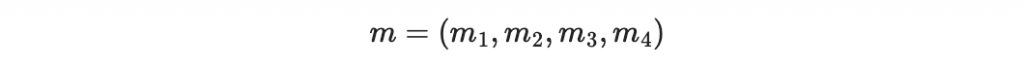
其奇偶檢查碼碼字為

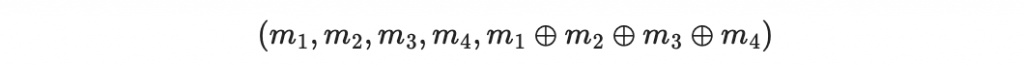
可以寫成以下的矩陣乘法

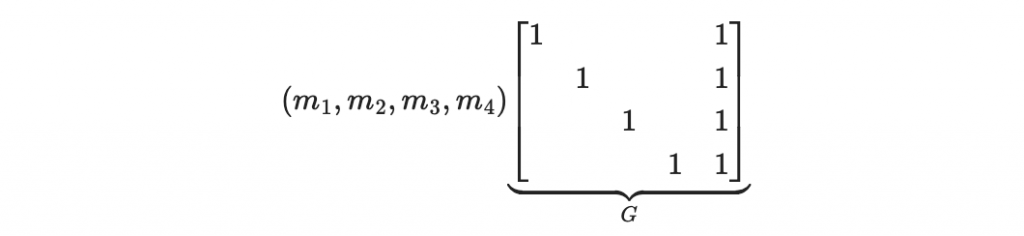
這個 G 就叫做該編碼方式的「生成矩陣」。

重複編碼

同樣地，假設訊息為

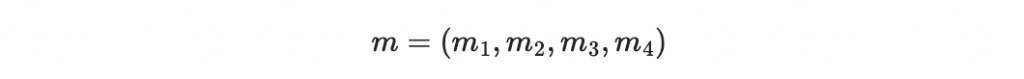
其重複編碼碼字為

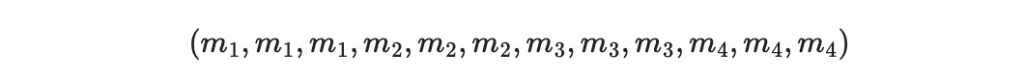
可以寫成

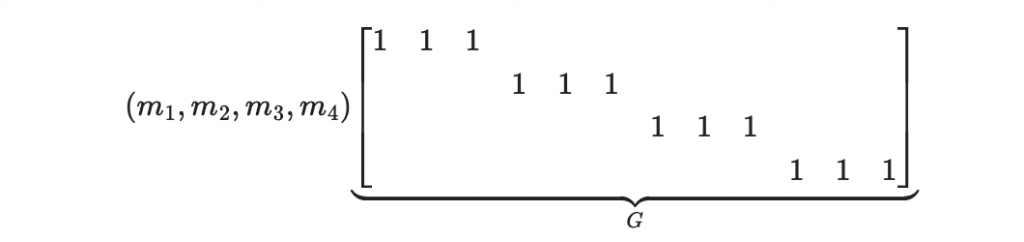
這個 G 就是重複編碼的「生成矩陣」

結論

生成矩陣 G 是 McEliece 密碼系統中的核心概念，因此我們首先介紹了這一點。明天的文章，我們將探討另一個重要的線性編碼——漢明編碼（Hamming Code），並了解如何檢查和定位錯誤。

ref:
GURUSWAMI, Venkatesan; RUDRA, Atri; SUDAN, Madhu. Essential coding theory.