漢明編碼是一種基本的錯誤更正碼（Error-Correction Code），他可以定位並更正一個錯誤。我們今天來詳細研究它：

漢明編碼 Hamming Code

延續昨日，假設我們有一個四位元的訊息要傳送

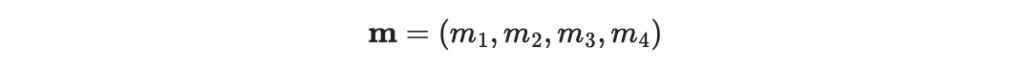
為了應對過程中可能產生的訊號干擾，我們昨天想到了「奇偶檢查碼」以及「重複編碼」等編碼方法，但他們各有優缺點......

Hamming Code 將以上訊息編碼為

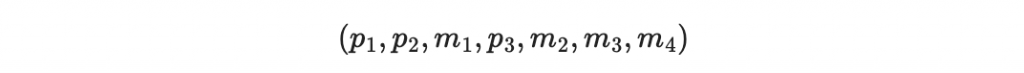
其中 p1 p2 p3 稱為「檢查碼」：

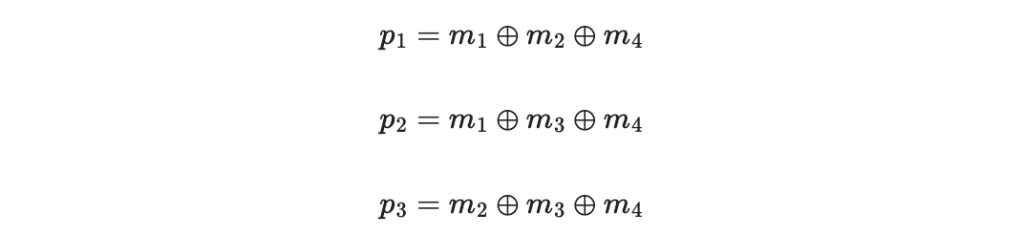
我們可以把這個編碼寫成生成矩陣

這樣訊息 m 的碼字就是 mG

好吧，那這個編碼的厲害之處在哪呢？

錯誤更正分析

假設碼字在傳遞過程中有一個位元發生錯誤，我們來分別看這個單位元錯誤會對碼字裡的檢查碼造成什麼效果

假設傳遞過程中是檢查碼出現錯誤，我們分情況做簡單的分析：

• 第一碼 p1 錯誤：
  則傳來的訊息是

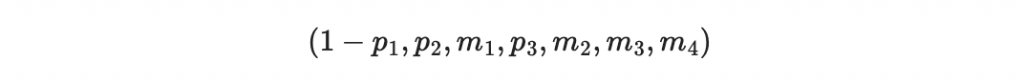
接收者可以根據收到的 m1, m2, m3, m4 來重新計算「收到後重算的檢查碼」 ，這個「收到後重算的檢查碼」因為訊息 m1 - m4 沒有出錯，所以就是初始的 p1, p2, p3 。因此我們有

進行同樣的分析：

• 第二碼 p2 錯誤：
  則傳來的訊息是

• 第四碼 p3 錯誤：
  則傳來的訊息是

有沒有發現一個規律！

把最右手邊的三元數組反向寫出來，你分別可以得到 001, 010, 100 ，這正好是 1, 2, 4 的二進位表示法！

這樣的巧合並不只有在檢查碼的位元發生，我們繼續做分析：

• 第三碼 m1 錯誤：
  則傳來的訊息是

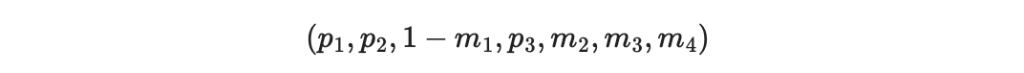
接收者現在根據收到的 1-m1, m2, m3, m4 計算「收到後重算的檢查碼」：

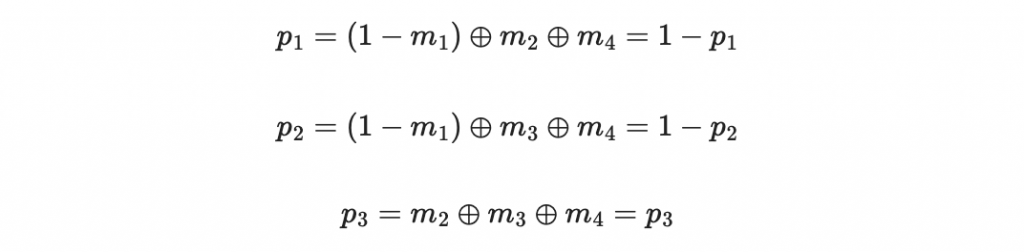
因此得到

（註解：很不好意思寫到這裡才說明，因為訊息都是以 0 與 1 表示，且我們使用的加法是異或運算（XOR）所以在這個世界 1 + 1 = 0 ）

• 第五碼 m2 錯誤：
  則傳來的訊息是

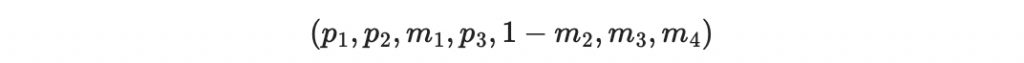
接收者現在根據收到的 m1, 1-m2, m3, m4 計算「收到後重算的檢查碼」：

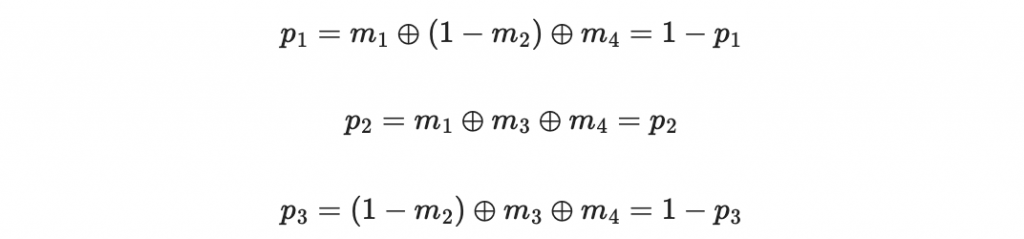
因此得到

把結果反著寫得到 101 ，也就是五的二進位表示法

• 第六碼 m3 錯誤：
  則傳來的訊息是

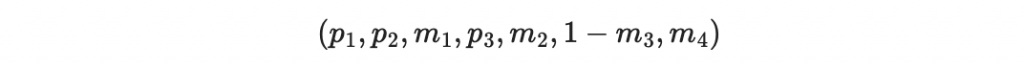
接收者現在根據收到的 m1, m2, 1-m3, m4 計算「收到後重算的檢查碼」：

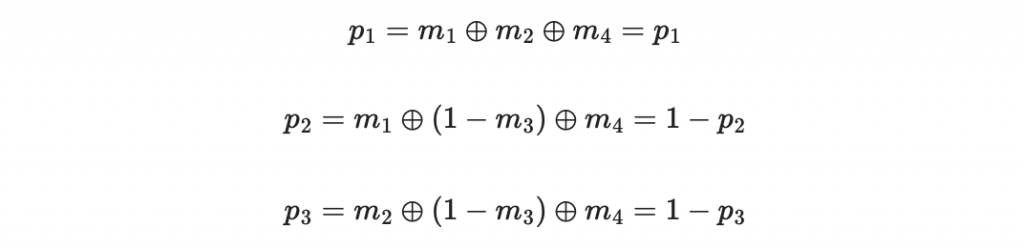
因此得到

把結果反著寫得到 110 ，也就是六的二進位表示法

• 第七碼 m4 錯誤：
  則傳來的訊息是

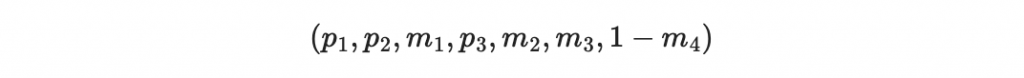
接收者現在根據收到的 m1, m2, m3, 1-m4 計算「收到後重算的檢查碼」：

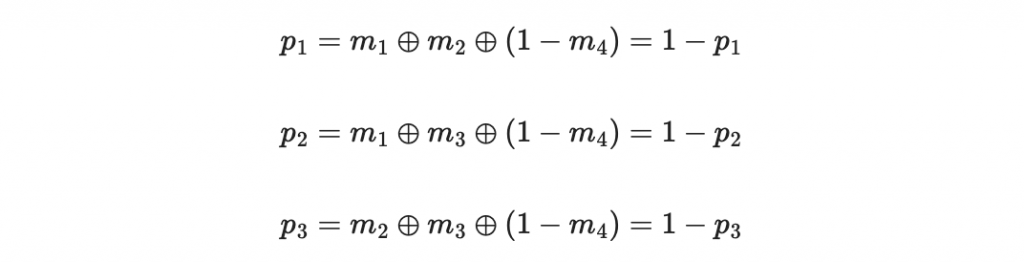
因此得到

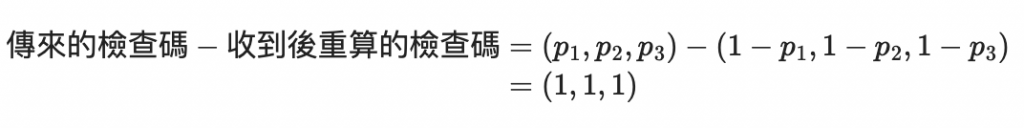
把結果反著寫得到 111 ，也就是七的二進位表示法

我們將這樣的分析總結在以下章節：

單一錯誤更正演算法

0. 傳送者將要傳送的訊息 m = (m1,m2,m3,m4) 進行編碼到碼字

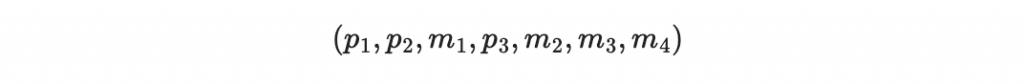
其中：

1. 接收者收到訊息，假設其中有一個位元發生錯誤，並將收到的訊息寫成

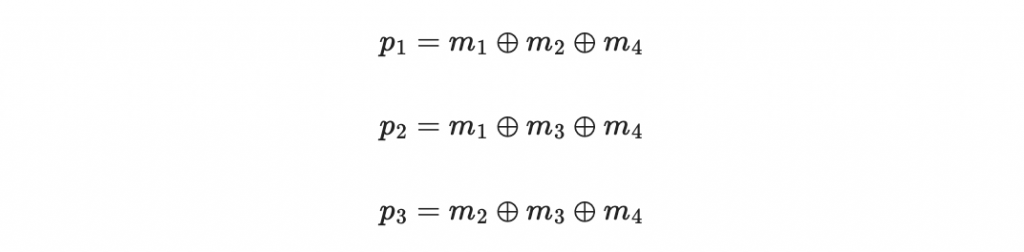
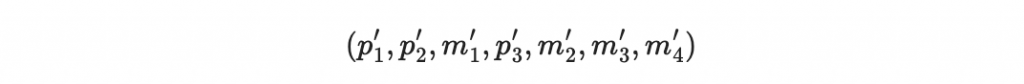
使用 m1', m2', m3', m4' 計算「收到後重算的檢查碼」，並將其與「收到的檢查碼」p1', p2', p3' 相減：

2. 將剛剛相減的結果（共三數字）反向寫出
3. 將反向寫出後的三數字做為二進位整數解釋，得到一個整數 n
4. 則此段傳來的碼字是在第 n 位元發生錯誤，將其更正之，於是得到正確訊息。

SageMath 實作

message = [randint(0, 1) for _ in range(4)]
print(f"原始數據: {message}")
 
# Outputs:
# 原始數據: [1, 1, 1, 0]

# 計算檢查碼

p1 = message[0] ^^ message[1] ^^ message[3]
p2 = message[0] ^^ message[2] ^^ message[3]
p3 = message[1] ^^ message[2] ^^ message[3]

# 組合碼字
codeword = [p1, p2, message[0], p3, message[1], message[2], message[3]]
print(codeword)

# Outputs:
# [0, 0, 1, 0, 1, 1, 0]

# random error
error_position = randint(0,6)
received = codeword.copy()
received[error_position] ^^= 1

print(f"錯誤位置（從1開始數）: {error_position+1}")
print(f"收到的碼字（有錯誤）: {received}")

# Outputs:
# 錯誤位置（從1開始數）: 4
# 收到的碼字（有錯誤）: [0, 0, 1, 1, 1, 1, 0]

# 重新計算檢查位
p1_re_calc = received[2] ^^ received[4] ^^ received[6]
p2_re_calc = received[2] ^^ received[5] ^^ received[6]
p3_re_calc = received[4] ^^ received[5] ^^ received[6]

print(f"收到的檢查碼: {received[0]}, {received[1]}, {received[3]}")
print(f"收到後重算的檢查碼: {p1_re_calc}, {p2_re_calc}, {p3_re_calc}")

# 相減並反向寫出
syndrome = [p1_re_calc ^^ received[0], p2_re_calc ^^ received[1], p3_re_calc ^^ received[3]]
print(f"診斷出錯誤位置: {syndrome[::-1]}")


# Outputs:
# 收到的檢查碼: 0, 0, 1
# 收到後重算的檢查碼: 0, 0, 0
# 診斷出錯誤位置: [1, 0, 0]

# 修正錯誤
syndrome_position = sum([v * 2**i for i, v in enumerate(syndrome)])
print(syndrome_position)

corrected = received.copy()
corrected[syndrome_position-1] ^^= 1
print(f"更正後的碼字: {corrected}")

# 提取原始數據
original = [corrected[2], corrected[4], corrected[5], corrected[6]]
print(f"提取的原始數據: {original}")
print(f"原始數據: {message}")

# Outputs:
# 4
# 更正後的碼字: [0, 0, 1, 0, 1, 1, 0]
# 提取的原始數據: [1, 1, 1, 0]
# 原始數據: [1, 1, 1, 0]

明天我們來看更加複雜的 Reed-Soloman 編碼！

Takeaway

• Hamming code 如何將訊息編碼
• Hamming code 如何發現並更正一個位元錯誤？