今天一樣是跟著助教來做傅立葉級數分析，不過要來畫看看三角波，而三角波長得像這樣：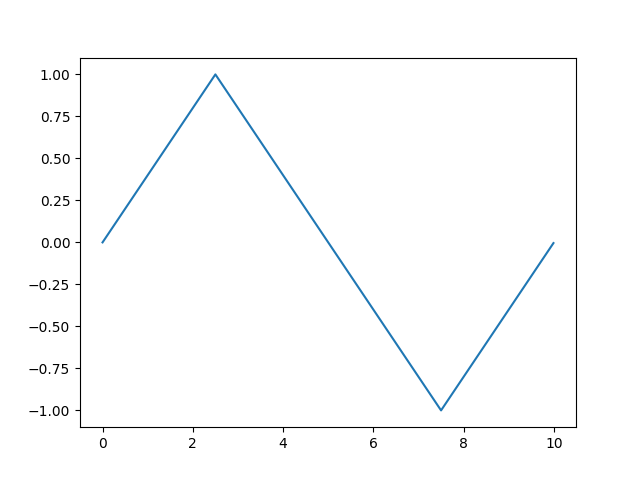

在波型建立上，我們會將一個週期內的三角波依照轉折點分成三份，先向上，再向下，最後再向上。

在python中是長這樣的：

import numpy as np
import matplotlib.pyplot as plt

#定義三角波
def triangular_wave(T, t): #T週期, t時間點
    # 切成三段 0~T/4, T/4~3T/4, 3T/4~T
    tinT = np.mod(t, T) #找出t在週期中是哪個階段，mod為餘數函數，取t除以Ｔ之後的餘數
    if tinT <= 0.25*T:
        return 1*tinT/(0.25*T)+0 #如果時間點位於週期0.25以內，則自0開始行進1*tinT/(0.25*T)
    elif 0.25*T < tinT <= 0.75*T:
        return -2*(tinT-0.25*T)/(0.5*T)+1#如果時間點位於週期0.25T~0.75T之間，則自位置1開始行進-2*tinT-0.25*T/(0.5*T)
    else:
        return 1*(tinT-0.75*T)/(0.25*T)+-1 #時間點位於0.75T~1T，則自-1開始行進1*(tinT-0.75*T)/(0.25*T)

#製圖精度
N = 1000

#定義週期
T = 10

#時間的最大值
t_max = T

#定義方波的高波比例
D = 0.5

#時間範圍
t_list = [t_max*i/N for i in range(N)]
#空間範圍
field_list = [triangular_wave(T, t_list[i]) for i in range(N)]

#兩個函數做內積（兩個函數相乘對空間做積分
#這裡直接將兩個函數的內容定義為陣列array去做對位相乘
def inner_product(list1, list2, dx):
    #先將兩筆函數內容list定義為array型式
    array1 = np.array(list1)
    array2 = np.array(list2)
    product = array1*array2*dx*2/t_max #乘以*2/t_max進行歸一化處理。
    return product.sum() #將相乘結果加總


#設定cos傅立葉級數
def Fourier_series_cos(field_list, n):
    cos_list = [np.cos(n*f0*t_list[i]) for i in range(N)]
    return inner_product(cos_list, field_list, T/N)

#設定sin傅立葉級數
def Fourier_series_sin(field_list, n):
    sin_list = [np.sin(n*f0*t_list[i]) for i in range(N)]
    return inner_product(sin_list, field_list, T/N)

#設定基礎頻率
f0 = 2*np.pi/T

#定義傅立葉級數序號，可自行帶入數值，這裏示範為100
n_max = 100
n_list = [i for i in range(n_max)]

#定義傅立葉級數轉換結果cos list
Fourier_series_list_cos = [Fourier_series_cos(field_list, n_list[i]) for i in range(n_max)]

#定義傅立葉級數轉換結果sin list
Fourier_series_list_sin = [Fourier_series_sin(field_list, n_list[i]) for i in range(n_max)]


#建立繪圖迴圈，以畫出級數範圍內n的組合圖，這裏以sin為例
plt.subplot(1,2,1)
plt.plot(t_list, field_list)
sum_array = np.zeros(N) #定義陣列及為陣列

for n in range(n_max):
    sin_list = [Fourier_series_list_sin[n]*np.sin(n*f0*t_list[i]) for i in range(N)]
    sin_array = np.array(sin_list) #將sin_list做成array
    sum_array += sin_array #加總arrays
    #plt.plot(t_list, sin_list)

plt.plot(t_list, sum_array, "--")

plt.subplot(1,2,2)
plt.bar(n_list, Fourier_series_list_sin)
plt.show()

傅立葉級數分析後，得出圖如下：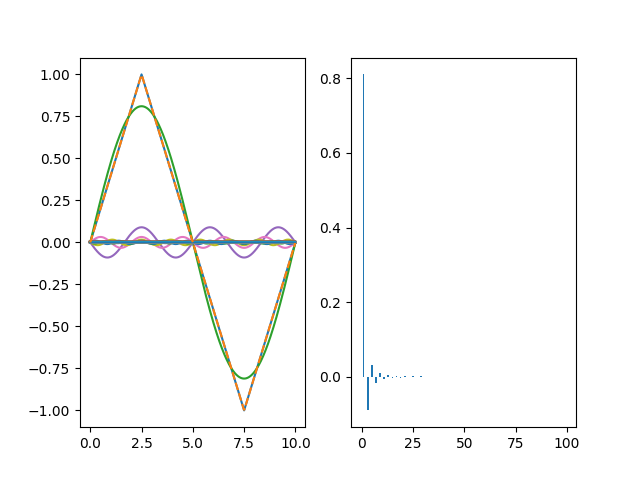

在模擬三角波過程中，我們自方波的程式碼改了以下內容：

1. 建立三角波程式
2. 對內積結果乘以*2/t_max 做歸一化處理
問chatGPT為什麼要歸一化呢？解釋如下：
2/t_max: 這個常數的作用是將內積結果與信號長度無關的量級進行調整，這樣內積的結果將與傅立葉級數的預期幅度匹配，並且能夠準確地表示信號在某個頻率成分上的強度。
3. sum_array那條顯示呈現為虛線，這單純是sum_array近似三角波效果太好了，兩者近乎重疊，只好改成虛線，才可以同時看出三角波和疊加的波型。

以上，感謝助教和AI，我感覺對傅立葉級數又更深入瞭解了：Ｄ