如題，今天將以最簡單的單狹縫為例，示範DFT離散傅立葉轉換分析的成果。

AI補充一下概念：
離散化（Discretization）是將連續的數學模型、數據或現象轉換為離散形式的一個過程。在許多科學和工程應用中，我們常需要處理連續的數據或方程，但電腦只能處理離散的數據，因此需要進行離散化。這個過程通常包括將連續的時間、空間或其他變量劃分成有限的離散點。

熱騰騰程式碼如下：

import numpy as np
import matplotlib.pyplot as plt


# 定義函數內積
def inner_product(list1, list2, dx):
    array1 = np.array(list1)
    array2 = np.array(list2)
    tmp = array1*array2*dx
    return tmp.sum()

# 定義單狹縫
def slit(x, w):
    if (D/2-w/2) < x <= (D/2+w/2): #D 是空間範圍，w 是狹縫寬度
        return 1/w  # 當 x 落在狹縫的範圍內時，得1/w  
    else:
        return 0 # 當 x 落在狹縫的範圍內時，得0

# 定義離散傅立葉轉換
# 將狹縫函數 input_list 從空間域轉換到頻域，計算每一個頻率成分對應的傅立葉係數
def DFT(input_list, x_list, dx):
    N = len(input_list) # N 是取樣點的數量
    output = []  
    for n in range(N): #建立取樣點迴圈
        k = 2*np.pi/D * n #k為空間頻率
        phi = [np.exp(complex(0, -k*x_list[i]))for i in range(N)] #phi是相位因子 ，帶入空間頻率和座標求出
        inner = inner_product(input_list, phi, dx) #內積結果，使空間頻率對應到每個頻率
        output.append(inner) #將每個取樣點的結果加入output中
    return output


#取樣點的數量
N = 501

#空間範圍
D = 10

#總波數範圍
K = N*2*np.pi/D

#狹縫寬度
w = 1
# 設定空間變數的列表
x_list = [i*D/N for i in range(N)]
kx_list = [i*K/N for i in range(N)]

# 計算單狹縫函數在空間中的分佈 ，然後對其進行離散傅立葉轉換，得到頻域的分佈 DFT_slit
slit = [slit(x_list[i], w) for i in range(N)]
DFT_slit = DFT(slit, x_list, 1/N)

# 畫圖
plt_phi1 = [slit[i] for i in range(N)]
plt_phi2 = [abs(DFT_slit[(i+int(N/2))%N]) for i in range(N)]

plt.subplot(1,2,1)
plt.plot(x_list, plt_phi1, label = 'slit')
plt.legend()
plt.subplot(1,2,2)
plt.plot(kx_list, plt_phi2, label = 'DFT')
plt.legend()
plt.show()

跑出圖如下：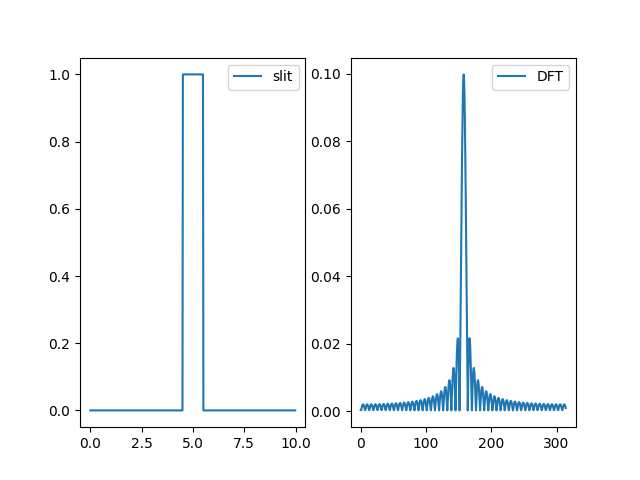

比較先前一維傅立葉轉換的圖（同狹縫規格）：

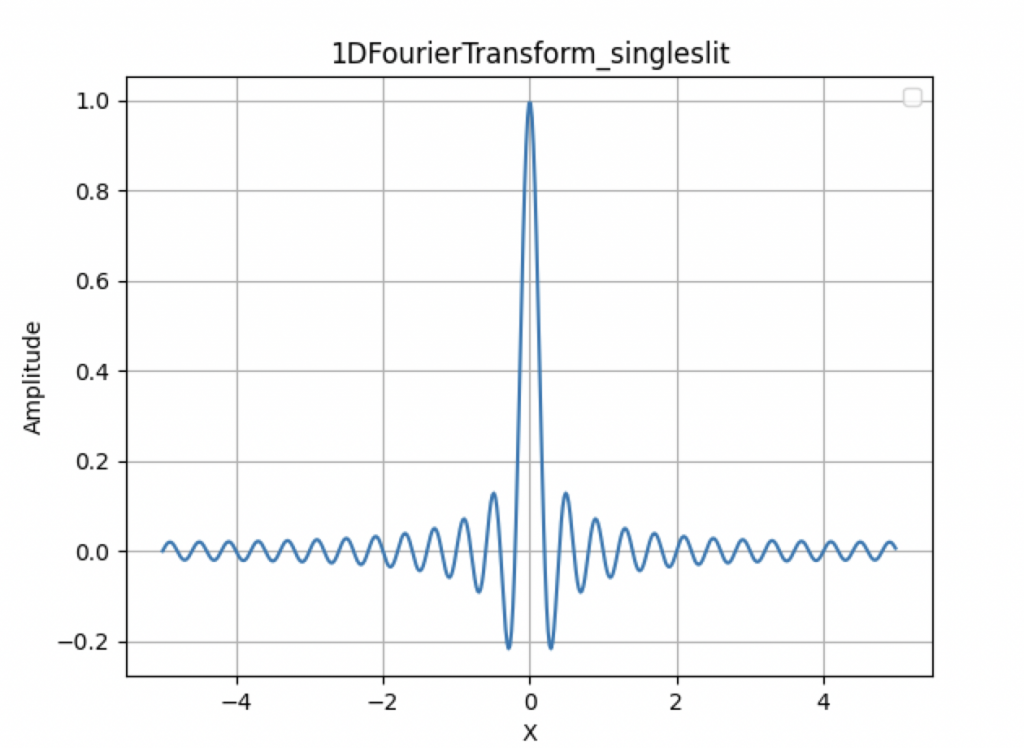
主要差異：

1. 計算方法:
   • 一維傅立葉轉換：使用數值積分計算Fraunhofer衍射圖樣，這是透過直接積分的方法。
   • 離散傅立葉轉換：使用離散傅立葉變換（DFT）來計算頻譜，是一種數值方法來近似傅立葉變換。
2. 頻域表示:
   • 一維傅立葉轉換：直接在空間域上呈現衍射圖樣。
   • 離散傅立葉轉換：呈現傅立葉轉換後的頻域，並顯示了衍射圖樣在頻域上的幅度。

這兩段程式碼都有效地展示了單狹縫的衍射現象，但採用了不同的數值方法來實現。第一段程式碼專注於數值積分的方法，而第二段程式碼則使用了離散傅立葉變換的數值計算方式。