Hey~ 這裡是鐵匠史密斯，
昨天我們聊到玩家的視線方向 fPlayerA 和視野範圍 AoV，
但只知道方向還不夠，今天我們要探討——方向的正負定義，以及如何用它計算玩家的單位向量，這可是 Ray Casting 的基礎之一!
為了怕大家混淆方向(角度)的正/負，我們來畫個圖，做簡單的比喻:

到底哪個方向角度是正/負?

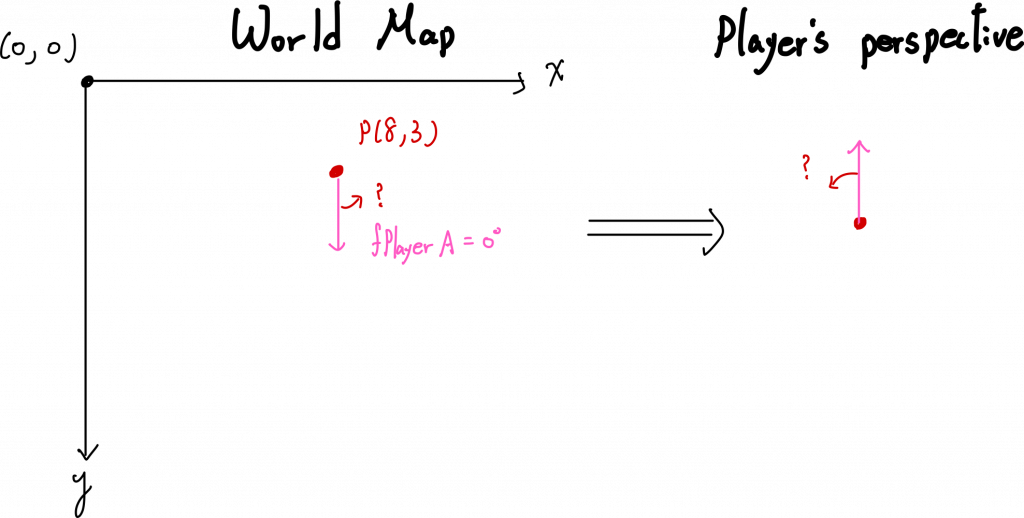
我們在玩家的視角，如果是向左邊旋轉，那角度是正的，還是負的呢?
好，我們旋轉個30 degree，查看一下狀態: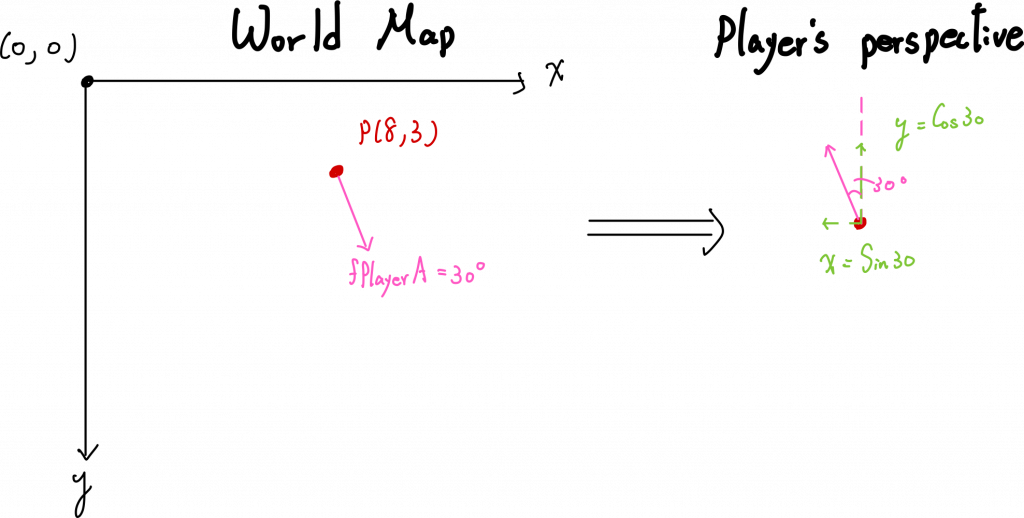

假設，我們在玩家的正視方向，向左旋轉30度，可以看到 x 分量、 y 分量為:
x = sin30
y = cos30
這是不是有一種既視感?
我們再看下一張圖:

這樣不就像是玩家正視角 fPlayerA = 0 像在笛卡爾 2-D 座標的 x 軸上，
並以逆時針30度旋轉玩家方向嗎?
那我們可以自己設立以下條件開發遊戲:

1. 遵守數學座標的定義: 以 玩家視角 0 度為基線，角度逆時針(Counterclockwise)為正、順時針(Clockwise)為負
2. 只是因計算機圖學座標系的影響，在這個專案中我們的水平方量x、垂直分量y的算法與數學座標剛好相反
   因為螢幕的 y 軸是向下遞增，而數學座標的 y 軸是向上遞增，這會影響三角函數分量的對應。

單位向量

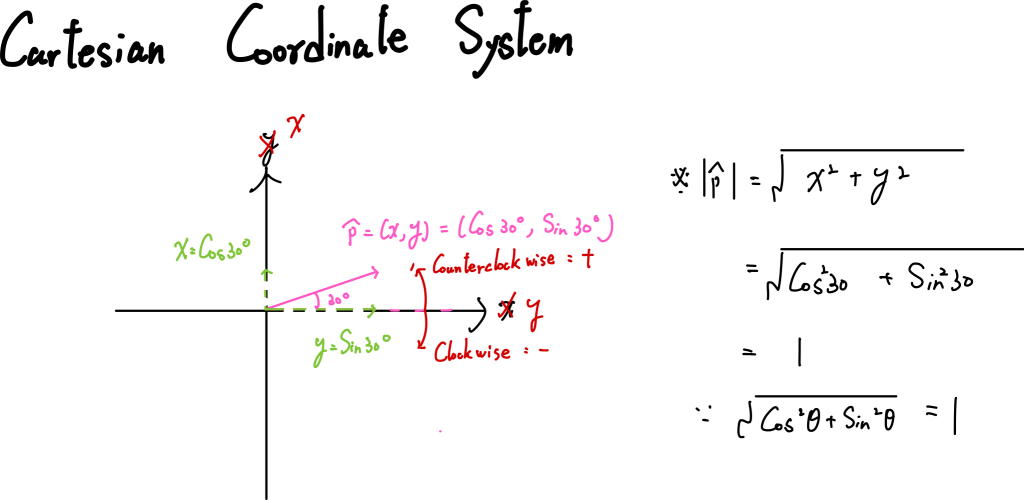
我們可以知道，在我們設計的遊戲中
x = sin30
y = cos30
x 、 y 方向，都有其大小，其可以組成向量

又因為三角函數的定理:

direction = sqrt(x^2 + y^2) = sqrt( cos30 * cos30 + sin30 * sin30) = 1

我們可以把當前玩家正視的方向，以角度可表示成玩家即將要前進的單位向量!
單位向量這個概念會在後面Ray Casting時會使用到~

今日總結

• 玩家旋轉角度的正/負定義
• 單位向量

遊戲背後的運作原理可不簡單啊~
今天的方向正負定義與單位向量雖然只是小小一步，但它們會在後面的 Ray Casting 中發揮大作用。
如果有錯誤，再請大佬們不吝指正~ 我們繼續走下去！