Hey~ 鐵匠史密斯又來了~
我們今天就來小補充一下如何求得左/右方向的單位向量吧!

如何求得左/右方向的單位向量?

由順時針為負，逆時針為正的規則可知:

• 玩家的正左單位向量(分量 x): sin(fPlayerA + pi/2)
• 玩家的正左單位向量(分量 y): cos(fPlayerA + pi/2)
• 玩家的正右單位向量(分量 x): sin(fPlayerA - pi/2)
• 玩家的正右單位向量(分量 y): cos(fPlayerA - pi/2)

其實就可以搭配三角函數的定理從上面的方式去修改程式碼了
不過，其實也有另一種方法，叫做旋轉矩陣
我們先上一張圖片:

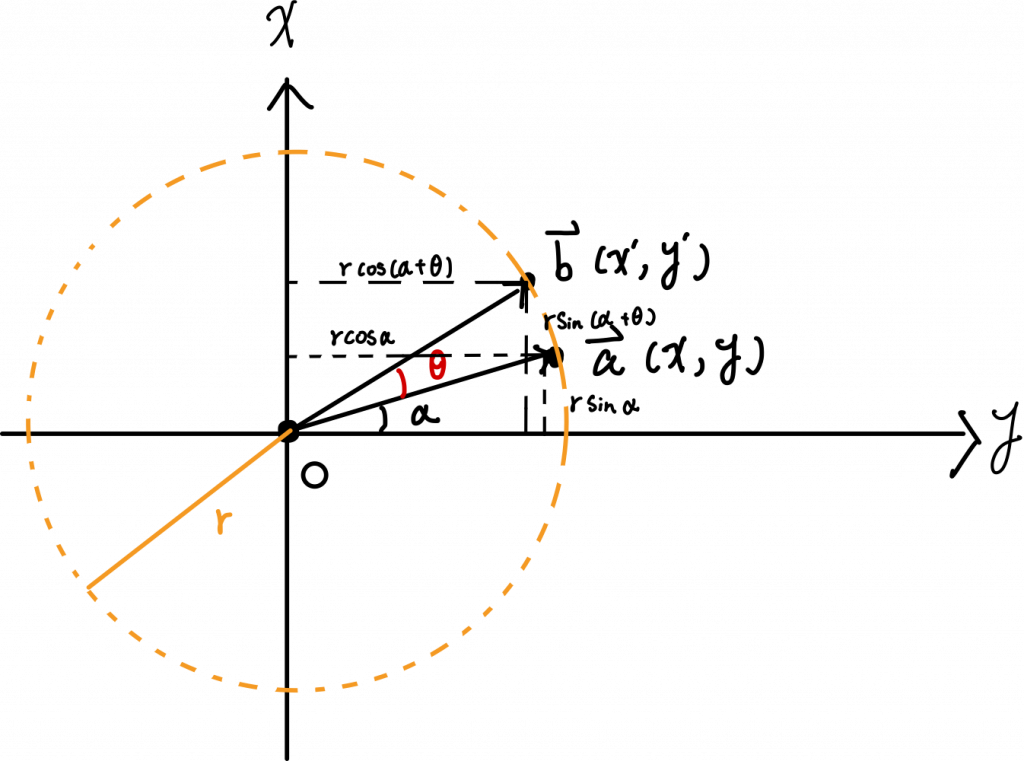
對的，這張圖就是以計算機圖學的座標進行繪製
假設，一開始有一個向量，其夾角為 α。
其實我們可以把**y軸 視為 fPlayerA = 0 延伸的軸線**
我們以幾何的方式來證明 α + θ 的新向量的 x 、 y 分量分別為多少:
當然，簡單的三角函式 - 和角公式就可以達成目的(可以參考 三角函式─公式證明)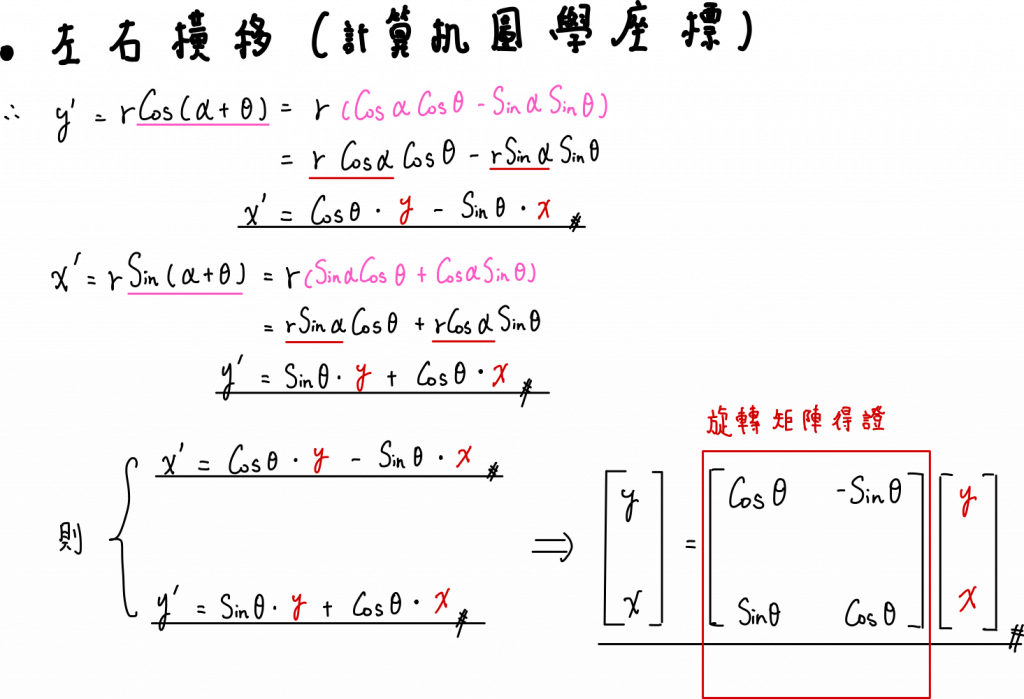

得出 x 、 y 分量後，我們就可以用矩陣表示原向量 (x, y) 與新向量 (x', y') 之間的差別 這個差別就可以用旋轉矩陣表示
p.s. 其實，這個旋轉矩陣之後可以另外寫成一個函示，這樣以後應用到一些特殊的場景(ex: 玩家精神異常、喝醉後，左/右 橫移的向量會改變等等)**

又我們在遊戲內得知:
玩家向量的水平分量: x = sinf(fPlayerA)
玩家向量的垂直分量: y = cosf(fPlayerA)

我們用旋轉矩陣就可以得知 原本玩家向量的角度fPlayerA 加上 +pi/2 以及 -pi/2 後的新向量─左向量、右向量的結果了

自然就可以將左/右向量的結果套用在我們的code 上啦

// Move Left&Right in the map
if (GetAsyncKeyState((unsigned short)'A') & 0x8000)
{
    fPlayerX += cosf(fPlayerA) * fElaspedTime * 5;
    fPlayerY -= sinf(fPlayerA) * fElaspedTime * 5;
}

if (GetAsyncKeyState((unsigned short)'D') & 0x8000)
{
    fPlayerX -= cosf(fPlayerA) * fElaspedTime * 5;
    fPlayerY += sinf(fPlayerA) * fElaspedTime * 5;
}

今日總結

• 左/右方向的單位向量可以直接用三角函數公式（± pi/2）求得
• 旋轉矩陣其實就是在數學上幫我們**「統一處理向量旋轉」**的工具，能更有系統地推導出 (x', y')
• 實作上，只要掌握「順時針為負、逆時針為正」的方向規則，就能正確算出 A / D 鍵的橫移效果

今天我們用旋轉矩陣拆解了「左右橫移」的向量計算，這其實是遊戲操作裡很重要的一環──因為只有能夠前後 + 左右移動，玩家才算真的能「自由走動」在 2D 世界裡。
明日我們要談論碰撞檢測(Collision Detection) 的概念
繼續走下去~

Reference

1. 三角函式─公式證明