MDP（馬可夫決策過程）
MDP 是一種數學框架，用來形式化描述「在不確定環境下，Agent 如何決策」的問題。
它包含：

（States 狀態集合） — 環境可能的狀態。
（Actions 行動集合） — Agent 可以採取的動作。
（轉移概率函數） — 做某動作後，從一個狀態轉移到另一狀態的機率。
（獎勵函數） — 每次行動後的即時回饋。
（折扣因子） — 決定未來獎勵的重要性。

Agent 為什麼要用 MDP？
MDP 的存在，是為了給 Agent 一個明確的決策遊戲規則。
可以想成：
Agent 是玩家
MDP 是遊戲的規則說明書
遊戲過程中，Agent 每回合根據當前的「狀態」選擇一個「動作」，然後 MDP 告訴你：
行動後會以什麼機率到哪個新狀態（P）。
你得到多少分數（R）。
在 MDP 框架下，Agent 與環境的互動循環是：

觀察狀態
例：自駕車現在的位置、速度、路況。
選擇動作
例：加速、減速、左轉、右轉。
環境回應：
根據轉移概率
決定新狀態
根據轉移概率𝑃(𝑠𝑡+1∣𝑠𝑡,𝑎𝑡)決定新狀態𝑠𝑡+1
根據獎勵函數𝑅(𝑠𝑡,𝑎𝑡)給 Agent 一個分數。
重複直到完成任務。
數學上這是一個：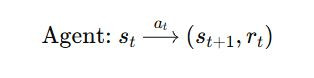

其中 P 和R 是由 MDP 定義好的。