特徵工程

如果我們要跟一個沒見過貓的朋友敘述貓的長相，我們正常不會說「他左上的第一個像素顏色是什麼」，而是敘述他的眼睛、耳朵、尾巴長怎麼樣。對電腦來說，讓他主動尋找一張影像中重要的部分，我們會稱之為特徵工程 (feature engineering)，他的目標是從原始的像素數據中，提取出這些有意義、有鑑別度的資訊。

特徵的需求

一個好的特徵，常會滿足以下幾個條件

1. 不變性 (invariant): 這是最重要的一點。無論物體在影像中如何移動（平移）、放大縮小（尺度變化）、旋轉，甚至在不同光照下，一個好的特徵都應該能被穩定地偵測出來。

2. 局部性 (locality): 特徵應該是局部的。這代表它是基於像素周圍的一個小區域計算出來的，而不是整張影像。這使得特徵對於遮擋或背景混亂的情況更具魯棒性。

3. 鑑別度 (distinctiveness): 特徵必須是獨特的，讓人可以輕易地將它與其他特徵區分開來。例如，牆壁上一片白中的某個點就沒有鑑別度，但書本的一個角就很有鑑別度。

4. 數量 (quantity): 一張影像中應該能偵測出足夠數量的特徵，以便能夠完整地描述影像內容。但數量也不宜過多，以免造成過大的計算負擔。

而角點 (corner) 就是一種非常優秀的特徵，它有著很高的鑑別度，並且在物體旋轉時能保持穩定，非常符合我們的需求。接下來，我們就來學習兩種最經典的角點偵測演算法。

Harris 演算法

假設我們在影像上放置一個小小的滑動窗口 ，那麼 Harris 角點偵測演算法是基於下面這三點

• 如果這個窗口在一片平坦的區域（如牆面），那麼無論你將窗口往哪個方向移動，窗口內的內容幾乎沒有變化。

• 如果窗口在一個邊緣上，當你沿著邊緣方向移動時，內容變化不大；但若垂直於邊緣移動，內容就會有劇烈變化。

• 如果窗口在一個角點上，那麼無論你朝哪個方向移動，窗口內的內容都會發生顯著的變化。

Harris 演算法基於這些事情，定義出了一個分數 R，公式為

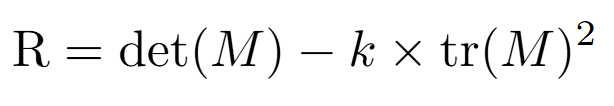
其中 M 是一個 2*2 的梯度矩陣，k 為一個常數。這時 R 的值會有三種情況

1. R > 0：代表是角點

2. R < 0：代表是邊緣

3. |R| ≒ 0：代表是平坦的區域

在 OpenCV，我們可以用 cv2.cornerHarris() 來簡單實現 Harris 演算法。

Shi-Tomasi 演算法

Shi-Tomasi 演算法改進了 Harris 演算法，如果是一個好的角點，那梯度矩陣 M 的兩個特徵值 λ1 跟 λ2 應該都要很大。因此我們只要取特徵值的較小的那一個

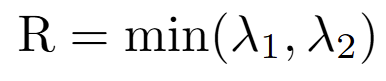
如果他大於設定的閾值的話，那代表他是一個好的角點。

在 OpenCV 內，Harris 跟 Shi-Tomasi 演算法分別可以以下程式碼實作

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取圖片，並轉換成灰階
img_bgr = cv2.imread('bird.jpg')
img_gray = cv2.cvtColor(img_bgr, cv2.COLOR_BGR2GRAY)
img_gray_float = np.float32(img_gray)

# Harris 角點偵測
harris_dst = cv2.cornerHarris(img_gray_float, 2, 3, 0.04)
harris_dst = cv2.dilate(harris_dst, None)

img_harris = img_bgr.copy()
threshold = 0.01 * harris_dst.max()
harris_points = np.where(harris_dst > threshold)

for y, x in zip(harris_points[0], harris_points[1]):
    cv2.circle(img_harris, (x, y), 5, (0, 0, 255), 2)
    cv2.circle(img_harris, (x, y), 2, (0, 255, 255), -1)

# Shi-Tomasi 角點偵測
corners = cv2.goodFeaturesToTrack(img_gray, 
                                  maxCorners=200,
                                  qualityLevel=0.01,
                                  minDistance=8)

img_shi_tomasi = img_bgr.copy()
if corners is not None:
    corners = corners.astype(int)
    for i in corners:
        x, y = i.ravel()
        cv2.circle(img_shi_tomasi, (x, y), 5, (0, 0, 255), 2)
        cv2.circle(img_shi_tomasi, (x, y), 2, (0, 255, 255), -1)

# 顯示結果
plt.figure(figsize=(18, 6))

plt.subplot(1, 3, 1)
plt.imshow(cv2.cvtColor(img_bgr, cv2.COLOR_BGR2RGB))
plt.title('Original Image')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(cv2.cvtColor(img_harris, cv2.COLOR_BGR2RGB))
plt.title(f'Harris Corner Detector ({len(harris_points[0])} corners)')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(cv2.cvtColor(img_shi_tomasi, cv2.COLOR_BGR2RGB))
plt.title(f'Shi-Tomasi ({len(corners) if corners is not None else 0} corners)')
plt.axis('off')

plt.tight_layout()
plt.show()

高斯差

Harris 和 Shi-Tomasi 都是優秀的角點偵測器，但它們有一個共同的弱點：它們對尺度變化很敏感。如果把相機拉遠，原本清晰的角點可能會變得模糊，導致偵測失敗。

為了解決這個問題，研究人員提出在「尺度空間 (scale space)」中尋找特徵。高斯差 (Difference of Gaussian, DoG) 就是一種高效實現尺度空間特徵偵測的方法。

它的原理是：

1. 對原始影像進行不同程度的高斯濾波，產生一系列模糊程度不同的影像（構成尺度空間）。

2. 將相鄰的兩張模糊影像相減。

3. 在這些相減後的差分影像中，尋找局部極值。

這些極值點，就是對尺度變化具有不變性的特徵點，通常被稱為「斑點 (blobs)」。斑點可以看作是角點的一種廣義形式。DoG 不僅是 SIFT 演算法中特徵偵測的基礎，其本身也是一種非常有效的特徵偵測器。