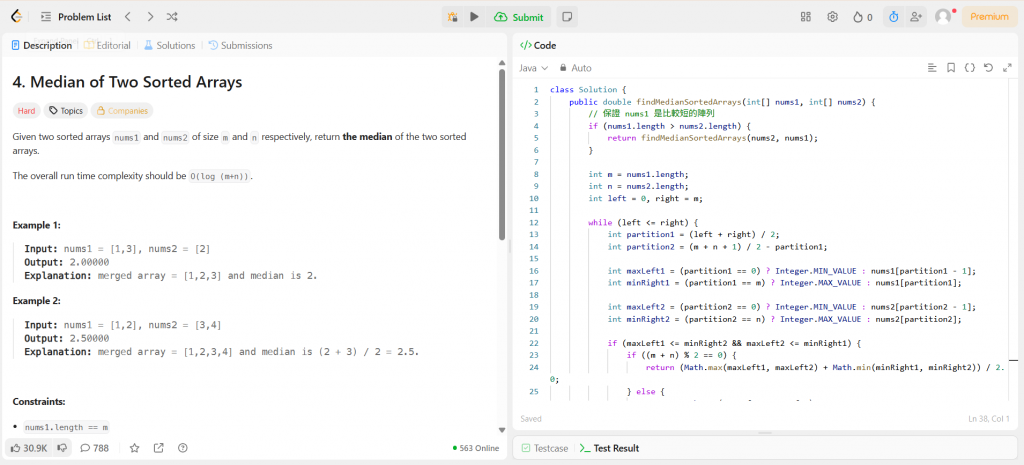
今天挑戰的是一題 Hard 題目：Median of Two Sorted Arrays。
題目很直白，就是給兩個已經排好序的陣列，要求我們找出合併後的中位數。

題目範例

Input: nums1 = [1,3], nums2 = [2]
Output: 2.0
因為合併後是 [1,2,3]，中位數是 2。

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.5
合併後 [1,2,3,4]，中位數是 (2+3)/2 = 2.5。

解題方向

題目要求時間複雜度要 O(log(m+n))，這代表不能直接合併兩個陣列再排序，因為那樣是 O(m+n)。

這裡要用「二分法 (Binary Search)」來處理：

我們想像把兩個陣列切開，左半邊和右半邊數量要平均。

保證左半邊的最大值 ≤ 右半邊的最小值。

中位數就會出現在「切口」附近。

做法是用 Binary Search 去調整切口的位置，直到符合條件。
這個演算法的細節比較 tricky，不過核心概念就是：

透過二分法控制 partition（分割點）。

最後根據陣列長度是奇數還是偶數，決定中位數的公式。

Java 程式碼
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
// 保證 nums1 是比較短的陣列
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}

    int m = nums1.length;
    int n = nums2.length;
    int left = 0, right = m;

    while (left <= right) {
        int partition1 = (left + right) / 2;
        int partition2 = (m + n + 1) / 2 - partition1;

        int maxLeft1 = (partition1 == 0) ? Integer.MIN_VALUE : nums1[partition1 - 1];
        int minRight1 = (partition1 == m) ? Integer.MAX_VALUE : nums1[partition1];

        int maxLeft2 = (partition2 == 0) ? Integer.MIN_VALUE : nums2[partition2 - 1];
        int minRight2 = (partition2 == n) ? Integer.MAX_VALUE : nums2[partition2];

        if (maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {
            if ((m + n) % 2 == 0) {
                return (Math.max(maxLeft1, maxLeft2) + Math.min(minRight1, minRight2)) / 2.0;
            } else {
                return Math.max(maxLeft1, maxLeft2);
            }
        } else if (maxLeft1 > minRight2) {
            right = partition1 - 1;
        } else {
            left = partition1 + 1;
        }
    }

    throw new IllegalArgumentException("Input arrays are not sorted properly.");
}

}

小心得

這題一開始看真的很頭痛，因為不像前幾題那樣能靠暴力法硬解。
關鍵是「用二分法切割陣列」，這樣才能達到 O(log(m+n)) 的複雜度。