題目說明

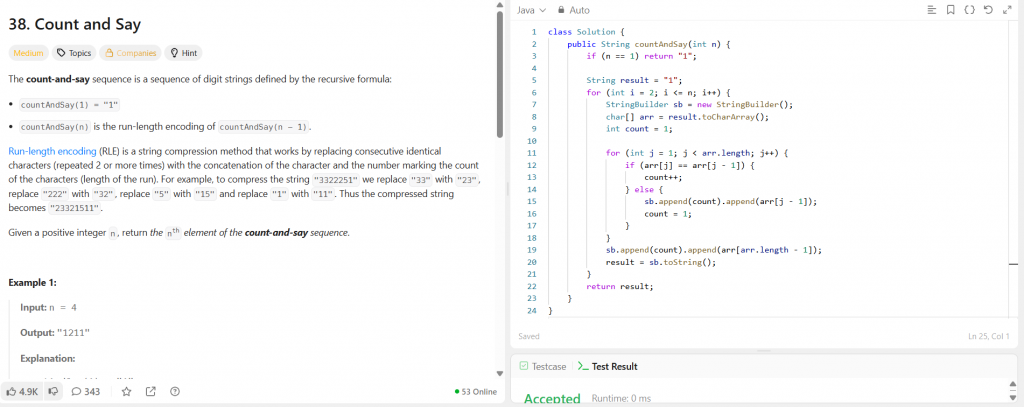
這題的重點是要產生 Count and Say 序列。
它是一個根據「上一項」描述「數字出現次數」的遞迴序列。

定義如下：

countAndSay(1) = "1"
countAndSay(n) = 對 countAndSay(n - 1) 進行“讀數描述”

也就是說每一項都要用「上一項」來產生。

範例解釋

以 n = 4 為例：

n countAndSay(n) 說明
1 "1" 基礎情況
2 "11" 一個 1 → "11"
3 "21" 兩個 1 → "21"
4 "1211" 一個 2、一個 1 → "1211"
類似「壓縮」的概念

這題其實就是在做 Run-Length Encoding (RLE)：
連續的相同數字用「數量 + 數字」表示。

例如：

"3322251" → "23321511"

兩個 3 → "23"

三個 2 → "32"

一個 5 → "15"

一個 1 → "11"

解題思路

這題適合用「迴圈 + 字串處理」來做。

步驟

從基礎 "1" 開始。

每次迴圈產生下一個字串：

用一個 StringBuilder 來建新字串。

從頭開始數相同數字有幾個。

把「數量 + 數字」加進結果中。

重複直到第 n 次。

Java 程式碼
class Solution {
public String countAndSay(int n) {
if (n == 1) return "1";

    String result = "1";
    for (int i = 2; i <= n; i++) {
        StringBuilder sb = new StringBuilder();
        char[] arr = result.toCharArray();
        int count = 1;
        
        for (int j = 1; j < arr.length; j++) {
            if (arr[j] == arr[j - 1]) {
                count++;
            } else {
                sb.append(count).append(arr[j - 1]);
                count = 1;
            }
        }
        sb.append(count).append(arr[arr.length - 1]);
        result = sb.toString();
    }
    return result;
}

}

複雜度分析

時間複雜度：O(n × m)，其中 m 為字串長度（每次生成都需掃一遍）

空間複雜度：O(m)，因為用 StringBuilder 存暫時結果

心得

這題是「字串處理」與「遞迴關係」的綜合練習。
雖然看起來像是壓縮問題，但重點是 理解前一項如何產生下一項。