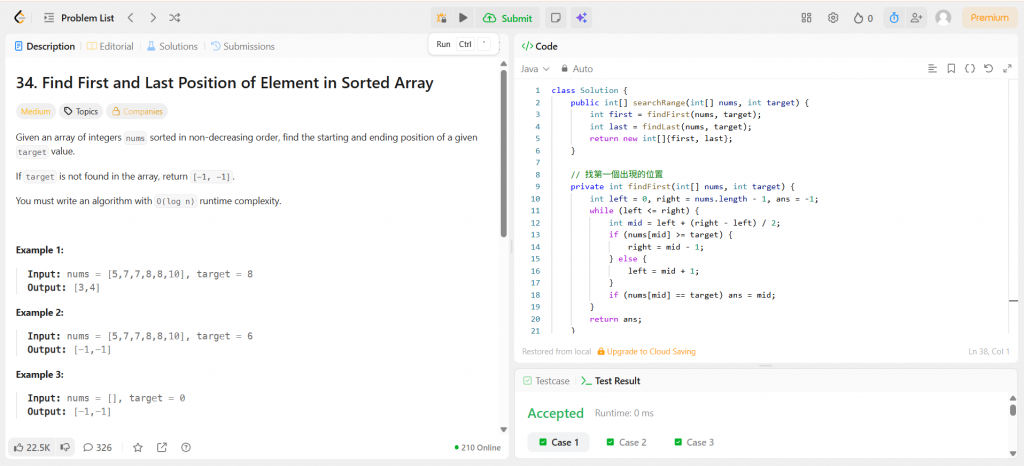
題目說明

給定一個 非遞減排序（升序） 的整數陣列 nums，找出目標值 target 出現的第一個與最後一個索引位置。
如果目標值不存在，回傳 [-1, -1]。

要求演算法的時間複雜度為 O(log n)。

範例
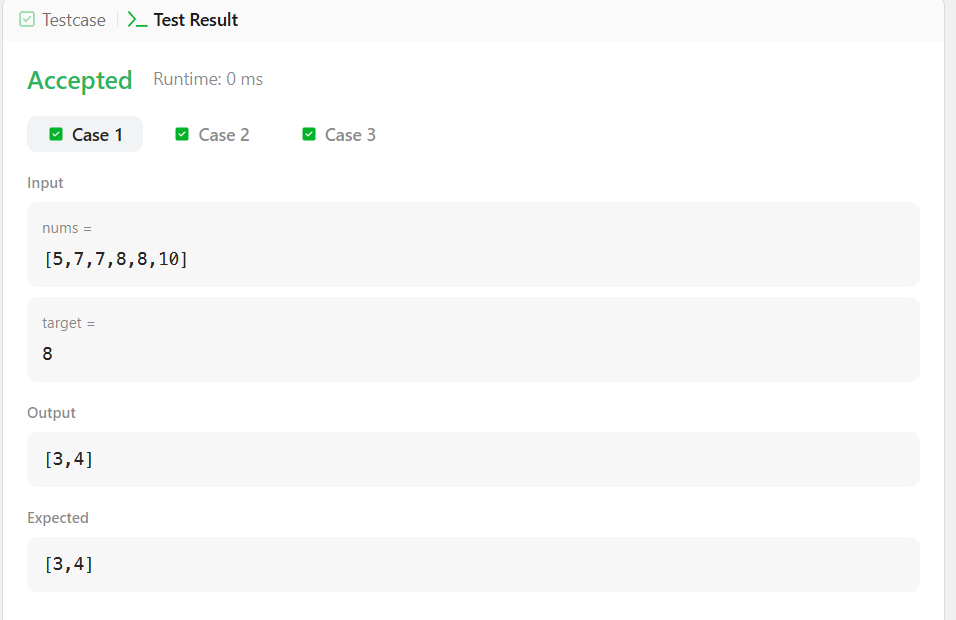
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

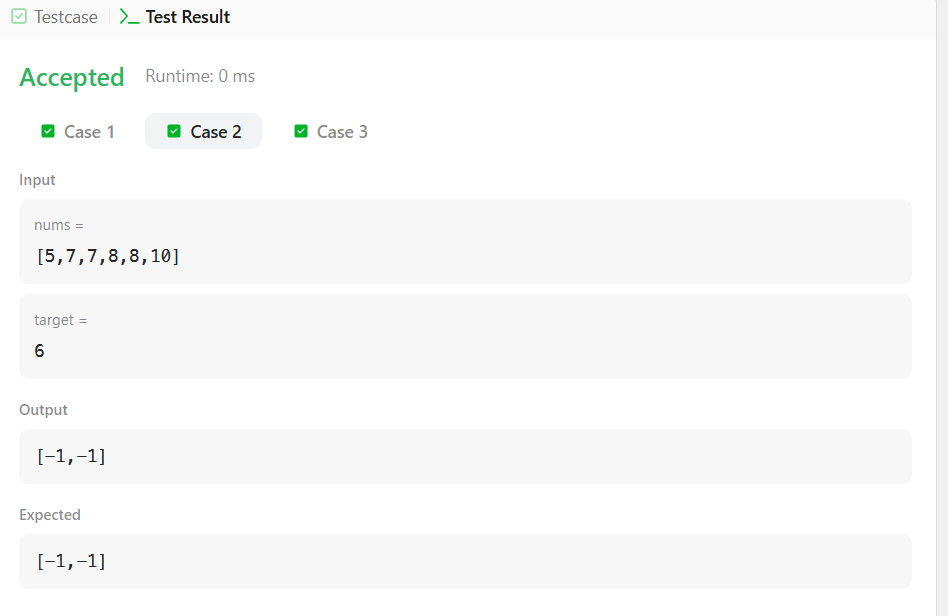
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

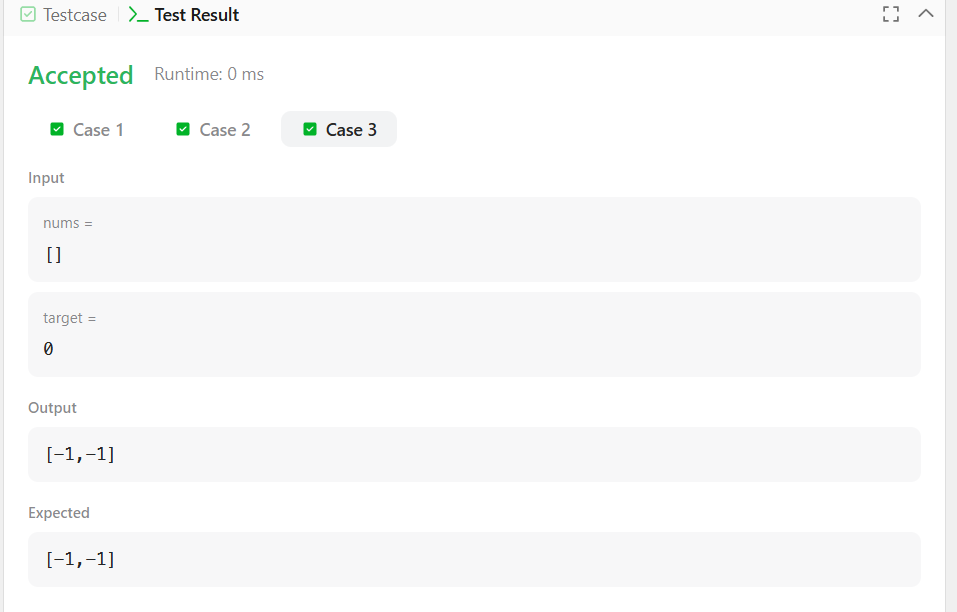
Input: nums = [], target = 0
Output: [-1,-1]

解題思路

這題要求 O(log n)，顯然要用 二分搜尋法 (Binary Search)。
不過這次不是找「單一值」，而是找「範圍」。

目標

我們要分別找出：

first position → 目標第一次出現的位置

last position → 目標最後一次出現的位置

這可以用兩次二分搜尋完成：

第一次找「第一個等於 target 的位置」

第二次找「最後一個等於 target 的位置」

步驟說明

使用二分搜尋。

每次遇到 nums[mid] == target：

如果是找「第一個出現」→ 繼續往左邊找（因為可能還有更前面）

如果是找「最後一個出現」→ 繼續往右邊找

若沒找到，回傳 [-1, -1]

Java 程式碼
class Solution {
public int[] searchRange(int[] nums, int target) {
int first = findFirst(nums, target);
int last = findLast(nums, target);
return new int[]{first, last};
}

// 找第一個出現的位置
private int findFirst(int[] nums, int target) {
    int left = 0, right = nums.length - 1, ans = -1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] >= target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
        if (nums[mid] == target) ans = mid;
    }
    return ans;
}

// 找最後一個出現的位置
private int findLast(int[] nums, int target) {
    int left = 0, right = nums.length - 1, ans = -1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
        if (nums[mid] == target) ans = mid;
    }
    return ans;
}

}

複雜度分析

時間複雜度：O(log n)（因為用了兩次二分搜尋）

空間複雜度：O(1)

心得

這題很適合熟悉「二分搜尋的變形」！
關鍵不是單純找某個數，而是找出「邊界位置」。