屬性基加密 (Attribute-Based Encryption)
屬性基加密 (ABE) 的概念，由 [SW05, GPSW06] 引入，是基於身份加密 (IBE) 的推廣。在 ABE 的一個主要變體中，密文是根據一組屬性 (attributes) 來加密的，並且主私鑰 (master secret key) 可用於為特定類別中的任何謂詞 (predicate) 生成私鑰。如果密文的屬性滿足某個私鑰的謂詞，那麼該私鑰就可以解密密文；否則，底層消息應保持隱藏。（基於身份的加密是特例，其中屬性對應身份（ID）的位元，而謂詞是與特定身份的相等性測試。）自 [GPSW06] 開始，許多基於允許雙線性配對 (bilinear pairings) 的密碼群體的 ABE 方案被設計出來。在 [GPV08, CHKP10, ABB10] 的基於格的基於身份加密方案出現後不久，這些系統的推廣也開始出現在屬性基的環境中。

25.2.1 ABE for Inner-Product Predicates
基於格的 ABE 的第一個例子是一個用於(相對比較大的)有限域 FF 上的 inner-product predicates 的系統，由 Agrawal、Freeman 和 Vaikuntanathan [AFV11] 提出，並經由 Xagawa [Xag13] 改進。該構造繼承了第 5.5.3 節描述的 [ABB10] 的 HIBE，但是針對一個謂詞的金鑰生成和解密涉及對主公鑰和密文的線性同態操作。在此描述這些構造的一個版本。

• 在上幾篇提到，對於質數 q，有限域 同構於一個特定的矩陣子環 。特別是，H 中任何兩個不同矩陣之間的差都是可逆的。

• 主公鑰 (master public key) 包含一個近似均勻隨機的 ，該矩陣使用陷門生成，一個均勻隨機的
  ，
  其中每個 的維度與小工具矩陣 G 相同，且 ℓ 是屬性向量在 F 上的長度；以及一個均勻隨機的綜合徵 (syndrome)  主私鑰 (master secret key) 是 的陷門。

• 對於一個屬性向量 定義矩陣
  以及
  
  要在屬性
  下加密一個位元 μ，我們只需像在對偶 LWE 密碼系統中一樣，向金鑰
  進行加密:
  
   (25.2.1)
  其中 s 是一個隨機的 LWE 秘密，近似關係隱藏了適當的小誤差，並且分量 分別對應於 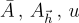正如預期的那樣。

• 要為一個謂詞向量  生成一個私鑰 ，使用 的陷門，定義短整數矩陣 
  
  定義
  
  並生成一個滿足下式的高斯分佈解 是
  

• 對於解密，觀察到對於任何 有 
  
  因此，要使用針對某個謂詞向量 滿足 的私鑰 來解密具有屬性向量 的密文
  計算
  
  並恢復 μ，其中的近似關係由方程式 (25.2.1) 成立，並且因為  和 是短的。另注意，如果 那麼 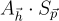會包含一個 G 的非零倍數與
  。這會阻止使用 進行解密。

在適當的 LWE 假設下，上述方案在選擇性屬性攻擊 (selective attribute attack) 下是語義安全的。在此類攻擊中，對手必須在見到主公鑰之前指定目標屬性向量 並且可以請求任何滿足 的謂詞向量， 所對應的私鑰。
安全性證明與第19篇中提到的數字簽章和基於身份的加密描述的證明密切相關，模擬器將其輸入樣本構造成矩陣 並將剩餘的主公鑰矩陣構造為 從而統計上隱藏了。

在這些矩陣中的標籤。此設置「穿刺 (punctures)」了公鑰，使得對於任何合法的謂詞查詢 滿足 。

參考資料
[SW05] A. Sahai and B. Waters. Fuzzy identity-based encryption. In EUROCRYPT, pages 457–473.
2005.

[GPSW06] V. Goyal, O. Pandey, A. Sahai, and B. Waters. Attribute-based encryption for fine-grained access control of encrypted data. In CCS, pages 89–98. 2006.

[GPV08] C. Gentry, C. Peikert, and V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In STOC, pages 197–206. 2008.

[CHKP10] D. Cash, D. Hofheinz, E. Kiltz, and C. Peikert. Bonsai trees, or how to delegate a lattice basis. J. Cryptology, 25(4):601–639, 2012. Preliminary version in Eurocrypt 2010.

[ABB10] S. Agrawal, D. Boneh, and X. Boyen. Efficient lattice (H)IBE in the standard model. In EUROCRYPT, pages 553–572. 2010.

[AFV11] S. Agrawal, D. M. Freeman, and V. Vaikuntanathan. Functional encryption for inner product
predicates from learning with errors. In ASIACRYPT. 2011.

[Xag13] K. Xagawa. Improved (hierarchical) inner-product encryption from lattices. In PKC, pages 235–252. 2013.