
不知道大家平常開發的時候,有沒有遇過這種狀況?一個看似正常的函式,當你試圖幫它撰寫單元測試時,卻發現需要模擬 API 資料、偽造 DOM、處理全域狀態...,簡直是場惡夢,很容易最後就頭痛的乾脆放棄了,這不是單純程式碼長度的問題,而是邏輯糾纏的問題——當一個函式試圖一次做太多不同性質的事情時,它的內部就形成了一團混亂的線球。若以前端的 React 開發來說,當一個元件裡面處理太多不同性質的事情時,也會讓我們感到頭痛而無法輕易去更動它。
在前幾篇文章中,我們已經建立了「不可變性 (Immutability)」以及將程式碼分類為 Actions、Calculations 和 Data (簡稱 ACD)的心智模型。不可變性是一種防禦性的策略,防止程式中的資料被意外的修改;而 ACD 模型則給了我們分析程式碼的依據,可透過這種方式來歸類並分析程式。
今天這篇想輕鬆點,介紹一點實務應用,看看如何用 ACD 模型,來將程式碼中混亂的計算邏輯和與外部世界的互動(也就是副作用)分離。雖然我們無法將所有程式都變成純函數,但是可以盡量提高純函數的比例,而擷取 Actions 中的 Calculations 就是一種提高純函數比例的方式。
如同先前文章提過的,Action 是任何會與其自身範疇之外的世界互動,或產生可觀測副作用的函式。現在來看一個常見的前端應用:購物車。
以下是這段程式碼會透過一個函式處理「新增商品至購物車」的邏輯,而這就是一個典型的 Action。
let shoppingCart = {
items: [{ id: 1, name: "簡約的軟體設計", price: 500, quantity: 1 }],
total: 500,
};
function handleAddItemToCart(itemToAdd) {
const existingItem = shoppingCart.items.find(item => item.id === itemToAdd.id);
if (existingItem) {
existingItem.quantity++;
} else {
shoppingCart.items.push({...itemToAdd, quantity: 1 });
}
let newTotal = 0;
for (const item of shoppingCart.items) {
newTotal += item.price * item.quantity;
}
shoppingCart.total = newTotal;
updateCartUI(shoppingCart);
}
這段程式看起來很正常,也有達到購物車的功能,看起來就像我以前會寫的程式(?😅,把所有要做的事都寫在一起 XD
但其實這段程式裡面耦合太多外部狀態,不符合 FP 純函數的原則,所以我們現在來看看它有哪些缺陷:
handleAddItemToCart(itemToAdd) 這個函式看似只依賴 itemToAdd 這一個參數,但實際上,它的行為完全取決於一個看不見的外部依賴——全域變數 shoppingCart。若不檢視函式的內部實作,任何人都無法僅從參數得知這個隱藏的依賴關係。shoppingCart 物件和呼叫 updateCartUI 來實現的。這些都是隱藏的副作用,程式碼的呼叫者無法預期執行這個函式會對系統的其他部分造成什麼反應。當一個函式隱性地讀寫共享狀態時,任何其他同樣讀寫該狀態的函式,都與它產生了隱性的耦合,這會增加開發者的認知負擔,並讓系統變得極度脆弱。
為了解決混雜 Action 的問題,解決方案的核心就在於「分離」。我們需要將函式中純粹的邏輯部分提煉出來,形成一個獨立、乾淨且可預測的單元。這個單元,我們稱之為「Calculation」,也就是前面提的純函數。
那要如何提取 Calculation 呢?
首先我們可以逐行為我們的程式標上標籤,標出他們屬於 Action、Calculation 還是 Data。
我將標示註解在程式旁如下:
// Action,全域變數的值會隨時改變,視為 Action
let shoppingCart = {
items: [{ id: 1, name: "簡約的軟體設計", price: 500, quantity: 1 }],
total: 500,
};
// Action
function handleAddItemToCart(itemToAdd) {
// Action:直接讀取全域變數 'shoppingCart'
const existingItem = shoppingCart.items.find(item => item.id === itemToAdd.id);
if (existingItem) {
// Action:直接修改全域狀態
existingItem.quantity++;
} else {
// Action:直接修改全域狀態
shoppingCart.items.push({...itemToAdd, quantity: 1 });
}
// Action 與 Calculation 混雜
let newTotal = 0;
for (const item of shoppingCart.items) {
newTotal += item.price * item.quantity;
}
shoppingCart.total = newTotal;
// Action
updateCartUI(shoppingCart);
}
接著我們需要找出這個函式的核心算式,將他抽離出來,我們可以審視 handleAddItemToCart 這個函式,並問自己:「這個函式最核心的決策邏輯是什麼?」
在 handleAddItemToCart 中,核心邏輯並不是更新 UI,也不是直接修改某個變數。它的核心邏輯是在回答一個問題:「給定一個『當前的購物車狀態』和一個『要加入的商品』,那麼『下一個購物車狀態』應該是什麼樣子?」
這個問題的答案,就是我們需要擷取出來的 Calculation。
我們來創建一個新的、純粹的函式,回答上述「給定一個『當前的購物車狀態』和一個『要加入的商品』,那麼『下一個購物車狀態』應該是什麼樣子?」這個問題。
// Calculation
function addItemToCart(cart, itemToAdd) {
//...
}
接著看一下我們預計如何實作 addItemToCart:
function addItemToCart(cart, itemToAdd):接收 cart 和 itemToAdd 兩個參數,透過明確的參數指出:「要完成我的工作,我需要一個購物車物件和一個商品物件。」,沒有任何隱藏的依賴。這個 addItemToCart 函式現在與 DOM、全域狀態、API 或任何系統的其他部分完全解耦。它是一個自給自足、封裝良好、只負責核心商業邏輯的黑盒子。我們可以放心地在任何地方使用它,而不用擔心它會產生意料之外的副作用。
addItemToCart 函式內部該如何實作? 在 addItemToCart(cart, itemToAdd) 函式中,我們要如何計算出新的購物車狀態,同時又不修改傳入的原始 cart 物件?
如果我們在函式內部寫:cart.items.push(...),就違背了「零副作用」的原則,而要解決這問題,就是要實現「不可變性」(Immutability),具體實現方式就是「寫入時複製」(Copy-on-Write),永遠不要修改既有的資料,而是先建立一個複本,然後在複本上進行修改。
addItemToCart以下為 addItemToCart 的實作以及註解說明。
// 採用「寫入時複製」模式實現的純粹 Calculation
function addItemToCart(originalCart, itemToAdd) {
// 檢查商品是否已存在於購物車中
const existingItemIndex = originalCart.items.findIndex(item => item.id === itemToAdd.id);
let newItems;
if (existingItemIndex > -1) {
// 情境一:商品已存在,增加數量
// 1. 建立 items 陣列的淺拷貝
newItems = [...originalCart.items];
// 2. 建立需要被更新的特定品項物件的複本
const updatedItem = {
...newItems[existingItemIndex], // 複製原有品項的所有屬性
quantity: newItems[existingItemIndex].quantity + 1, // 覆寫 quantity 屬性
};
// 3. 在新的陣列複本中,用更新後的品項複本替換掉舊的品項
newItems[existingItemIndex] = updatedItem;
} else {
// 情境二:商品為新品,直接加入
// 1. 建立 items 陣列的複本,並在末尾加入新商品
const newItem = {...itemToAdd, quantity: 1}
newItems = [...originalCart.items, newItem];
}
// 4. 根據全新的 items 陣列,重新計算總價
let newTotal = 0;
for (const item of newItems) {
newTotal += item.price * item.quantity;
}
// 5. 回傳一個全新的購物車物件,組合所有新的資料
return {
items: newItems,
total: newTotal,
};
}
如果要將函式內的邏輯抽得更乾淨,計算總價的那段程式碼可以再另外抽成 calcTotal 這個 Calculation,不過這裡就先不繼續細部拆分。
addItemToCart讓我們看看改使用 addItemToCart 的 handleAddItemToCart 長什麼樣子。
let shoppingCart = {
items: [{ id: 1, name: "簡約的軟體設計", price: 500, quantity: 1 }],
total: 500,
};
// 重構後、被簡化的 Action
function handleAddItemToCart(itemToAdd) {
// 步驟 1:將所有決策邏輯委派給純粹的 Calculation。
// Action 本身不知道、也不關心新的購物車狀態是如何計算出來的。
const newCartState = addItemToCart(shoppingCart, itemToAdd);
// 步驟 2:執行單一、明確的副作用——更新全域狀態。
// 這是整個應用程式中唯一一處修改 shoppingCart 的地方。
shoppingCart = newCartState;
// 步驟 3:執行其他副作用,例如更新 UI。
updateCartUI(shoppingCart);
}
目前我們將計算的邏輯搬到 addItemToCart,但是 shoppingCart 還是屬於全域變數,handleAddItemToCart 引用外部變數 shoppingCart 仍然屬於一種隱性輸入,因此更好的方式是讓 shoppingCart 作為參數傳入。
shoppingCart 作為參數傳入將 shoppingCart 作為參數傳入,並明確傳回新的購物車資料,改寫後如下。
let shoppingCart = {
items: [{ id: 1, name: "簡約的軟體設計", price: 500, quantity: 1 }],
total: 500,
};
// 重構後、被簡化的 Action
function handleAddItemToCart(cart, itemToAdd) {
const newCart = addItemToCart(cart, itemToAdd); // cart 透過參數傳遞
// 執行其他副作用
updateCartUI(newCart);
return newCart // 明確回傳更新後的購物車資料
}
// 實際呼叫 handleAddItemToCart 再傳入 shoppingCart
handleAddItemToCart(shoppingCart, itemToAdd);
目前重構到這告一段落,看一下完整改寫後的程式如下。
let shoppingCart = {
items: [{ id: 1, name: "簡約的軟體設計", price: 500, quantity: 1 }],
total: 500,
};
// Calculation
function addItemToCart(originalCart, itemToAdd) {
const existingItemIndex = originalCart.items.findIndex(item => item.id === itemToAdd.id);
let newItems;
if (existingItemIndex > -1) {
newItems = [...originalCart.items];
const updatedItem = {
...newItems[existingItemIndex],
quantity: newItems[existingItemIndex].quantity + 1,
};
newItems[existingItemIndex] = updatedItem;
} else {
const newItem = {...itemToAdd, quantity: 1}
newItems = [...originalCart.items, newItem];
}
let newTotal = 0;
for (const item of newItems) {
newTotal += item.price * item.quantity;
}
return {
items: newItems,
total: newTotal,
};
}
// Action
function handleAddItemToCart(cart, itemToAdd) {
const newCart = addItemToCart(cart, itemToAdd);
updateCartUI(newCart);
return newCart
}
// 實際呼叫 handleAddItemToCart 再傳入 shoppingCart
handleAddItemToCart(shoppingCart, itemToAdd);
雖然 handleAddItemToCart 目前還是一個 Action,因為它還是有更新 UI 造成副作用,但我們有成功擷取出一個純函數 Calculation 了! 並且將 shoppingCart 作為參數傳遞,減少了 handleAddItemToCart 的隱性輸入和輸出。
上面的案例中,我們以「減少隱性輸入與輸出」的原則完成重構,抽取出 Action 中的 Calculation。而「最小化隱性輸入與輸出」就是重構時的一個核心指導原則。
一個有著隱性輸入與輸出的函式,就像一個被焊死在機器上的零件,它的行為完全由周圍的其他部分決定,無法輕易地被拆卸下來單獨檢視或裝到別的機器上。相反地,當我們將這些隱性的依賴關係轉為明確的參數與回傳值時,就等於是為這個零件裝上了標準的接口,賦予了它「模組化」的特性。
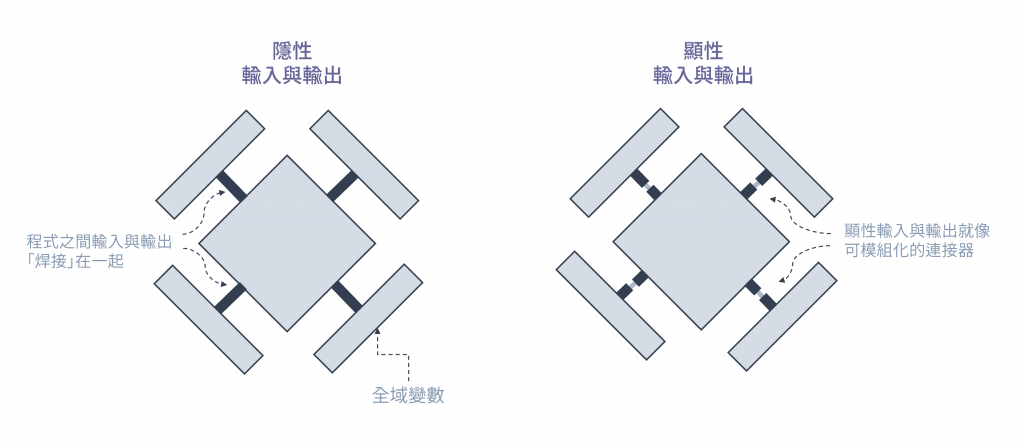
圖 1 最小化隱性輸入與輸出為程式帶來模組化特性(資料來源: 自行繪製)
這種缺乏模組化的特性會限制我們呼叫函式的時機。
這些限制降低了程式碼的可重複使用性。一個被「焊死」在特定 DOM 結構和全域變數上的函式,很難被應用到新的場景中。同樣地,這也讓邏輯的驗證變得困難。隱性輸入與輸出越多,我們在驗證函式正確性時需要準備的前置作業和需要檢查的後續影響就越多。這也是為什麼純粹的 Calculation 如此容易測試——它沒有任何隱性的依賴,給定輸入,驗證輸出即可。
因此,在重構的過程中,我們可以將「減少隱性輸入與輸出」作為一個指導原則,以此提升程式碼的可重複使用性,讓我們寫出更具模組化、更可靠的程式。
小小總結今天的重構案例,我們從一個包含各種任務的單一函式出發,最終將它其轉化為一個由兩個不同元件組成的、富有彈性的系統:一個是包含了我們所有複雜商業邏輯的、純粹的 Calculation;另一個則是負責與外部世界協調互動的 Action。
簡單列下這次重構的幾個核心觀念,如果之後大家想重構程式不知道如何下手的,可以參考看看:
大家有空的話可以在自己專案的程式碼中尋找,看看那些做了太多事情的函式,那些既在計算又在執行副作用的函式。然後問自己一個關鍵問題:「這個函式正在做出的核心決策是什麼?」一旦找到答案,就可以將那個決策邏輯提取到一個純粹的 Calculation 中。
當我們提取越多的 Calculation,我們程式中的 Calculation 比例就會越高,也會越好管理副作用,這就是 FP 程式設計師所注重的思維。
