題目簡介

題目要我們自己實作一個簡化版的正則表達式比對。給定一個字串 s 和一個模式 p，規則如下：

. 可以匹配任何一個字元

• 可以匹配前一個字元零次或多次

要求：必須完全匹配整個字串，而不是部分比對。

例子：

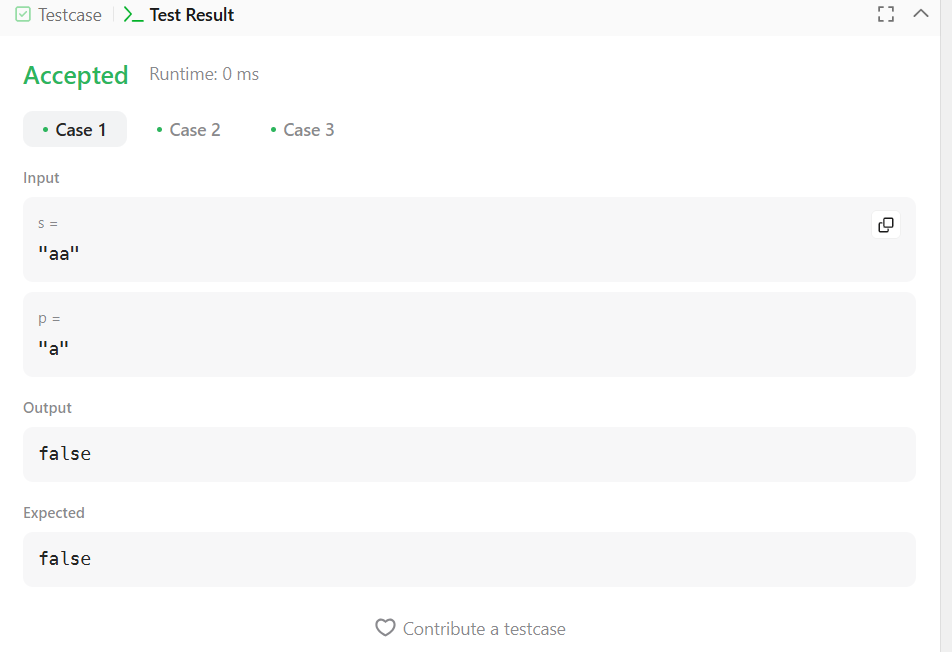
s = "aa", p = "a" → false

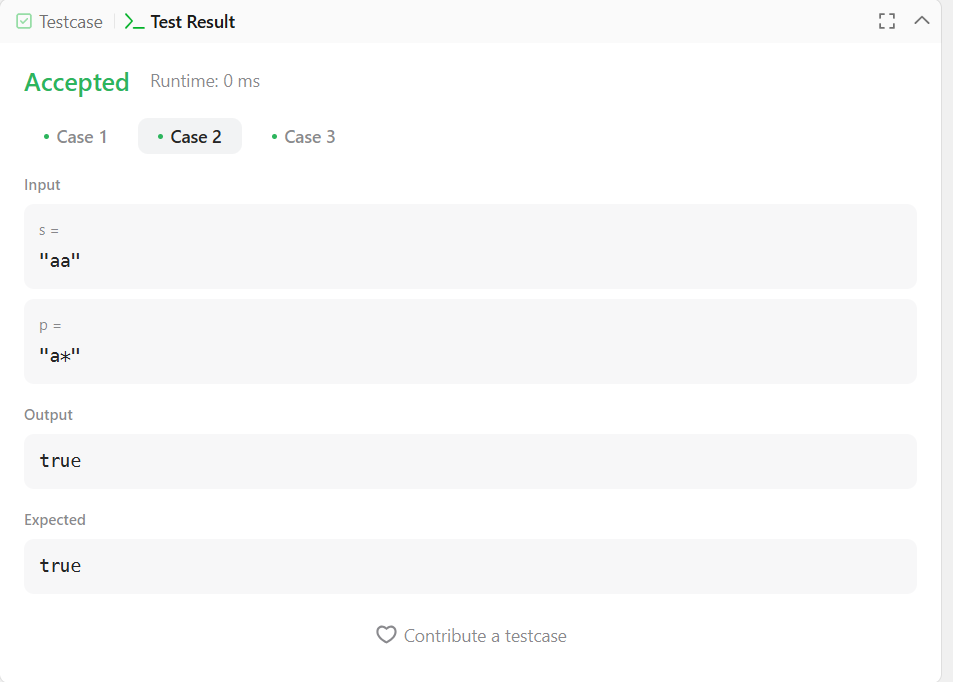
s = "aa", p = "a*" → true

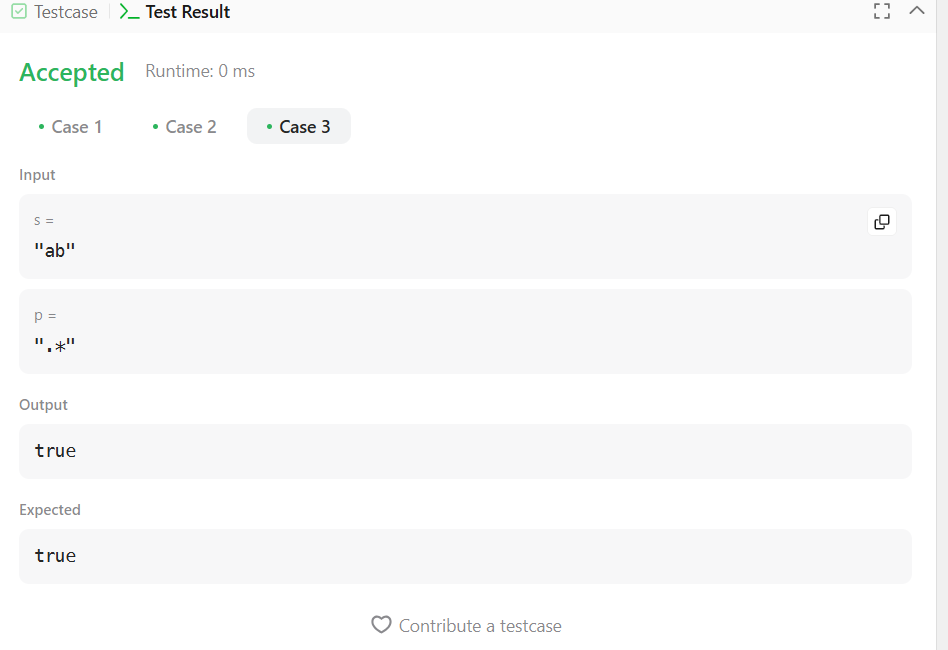
s = "ab", p = ".*" → true

思路

這題難度在於 * 的靈活性：

a* 可以代表 ""（0 次）或 "a", "aa", "aaa"...

所以遇到 *，要考慮「跳過前一個字元」或「繼續匹配前一個字元」。

解法有幾種：

遞迴 (回溯) → 實現容易，但效率差。

動態規劃 (DP) → 最佳解，時間複雜度 O(m × n)，其中 m, n 分別是 s 和 p 的長度。

DP 思路：

定義 dp[i][j] 表示 s[0..i-1] 是否能和 p[0..j-1] 匹配。

遞推關係：

如果 p[j-1] 是一般字元或 .：
dp[i][j] = dp[i-1][j-1] && (s[i-1] == p[j-1] 或 p[j-1] == '.')

如果 p[j-1] == '*'：

忽略 * 和前一個字元：dp[i][j] = dp[i][j-2]

或者繼續匹配：dp[i][j] = dp[i-1][j] && (s[i-1] == p[j-2] 或 p[j-2] == '.')

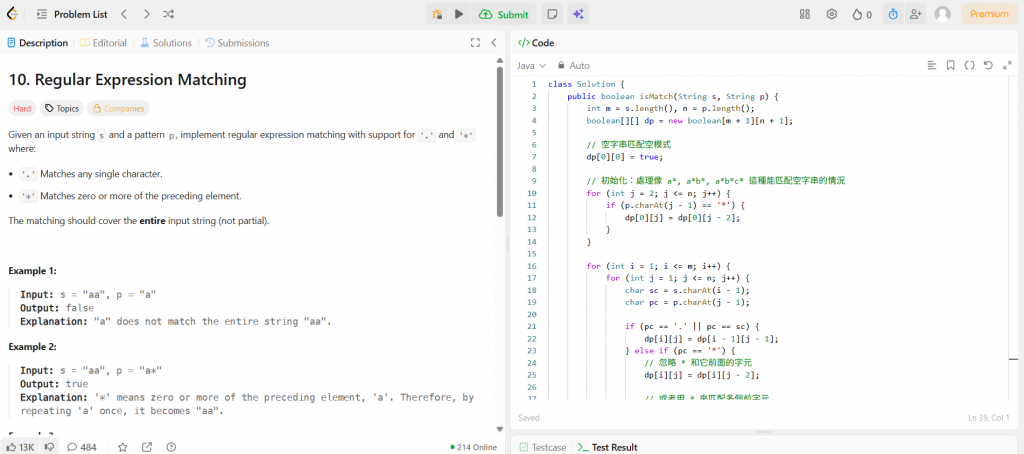
程式碼 (Java)
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length(), n = p.length();
boolean[][] dp = new boolean[m + 1][n + 1];

    // 空字串匹配空模式
    dp[0][0] = true;

    // 初始化：處理像 a*, a*b*, a*b*c* 這種能匹配空字串的情況
    for (int j = 2; j <= n; j++) {
        if (p.charAt(j - 1) == '*') {
            dp[0][j] = dp[0][j - 2];
        }
    }

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            char sc = s.charAt(i - 1);
            char pc = p.charAt(j - 1);

            if (pc == '.' || pc == sc) {
                dp[i][j] = dp[i - 1][j - 1];
            } else if (pc == '*') {
                // 忽略 * 和它前面的字元
                dp[i][j] = dp[i][j - 2];

                // 或者用 * 來匹配多個前字元
                char prev = p.charAt(j - 2);
                if (prev == '.' || prev == sc) {
                    dp[i][j] = dp[i][j] || dp[i - 1][j];
                }
            }
        }
    }

    return dp[m][n];
}

}

測試
Input: s = "aa", p = "a" → false
Input: s = "aa", p = "a*" → true
Input: s = "ab", p = "." → true
Input: s = "mississippi", p = "misisp." → false
Input: s = "mississippi", p = "misisip*." → true

心得

這題是名副其實的 Hard，我覺得難點主要在：

你要很清楚「*」代表什麼意思（零次 or 多次）。

DP 的狀態轉移要寫對，不然會有一堆 corner case。

這題做完感覺像打了一場硬仗，但也讓我更熟悉了 DP 的思考方式，特別是「定義狀態 → 找轉移」