
今天要介紹的是函數組合(Function Composition)~
在開始探索函數組合(Function Composition)的概念之前,先從一個生活一點的案例開始,假設我們要製作一份美味的下午茶,最簡單的就是泡一杯紅茶,只需要一個動作就能得到一個結果,但如果今天的目標是製作一個層次豐富、口感細膩的「法式抹茶慕斯蛋糕」呢?(抹茶真的好好吃...)

圖 1 法式抹茶慕斯蛋糕(資料來源: ChatGPT)
這個過程會是一連串環環相扣的步驟:
每一個步驟都需要以前一個步驟的產出為基礎。我們不能在烘烤蛋糕之前就開始組裝,也不能在冷藏定型之前就進行裝飾。這是一個嚴格的線性流程。
現在我們將這個烘培蛋糕的場景轉換到程式設計的世界。一個簡單的資料轉換,就像泡一杯紅茶一樣直接,但當我們面對一個複雜的業務需求——例如,從一個龐大的使用者資料中,篩選出活躍使用者,提取他們的個人資料,格式化地址,並生成一份客製化的報告——我們的程式碼就會像製作抹茶蛋糕一樣,充滿了連續的、有依賴性的處理步驟。
這就引出了一個問題:我們要如何組織我們的程式碼,來清晰又優雅地表達這一連串的處理流程?我們如何將這些獨立的步驟(函數)串連起來,形成一個資料處理管道,而不會迷失在連接每個步驟的繁瑣細節中?
在許多傳統的程式寫法中,真正造成混亂的,往往不是單一步驟(函數)本身的複雜度,而是連接這些步驟時所產生的繁瑣細節。這些用於手動連接的程式碼,無論是以層層嵌套的函數呼叫形式出現,還是以一系列臨時變數的形式存在,都迫使我們手動管理資料在不同處理單元之間的流動。這種手動管理不僅增加了程式的認知負擔,更提高錯誤發生的機率。
那該如何解決呢?今天要介紹的「函數組合 (Function Composition)」就是為了解決連接流程的問題而生的,它讓我們能以更優雅、明確的方式處理一連串的線性邏輯。
先來看幾個日常開發會見到的例子~
要如何處理線性的處理邏輯呢?最直觀的方式就是將一個函數的呼叫結果,直接作為下一個函數的參數。當流程只有兩三步時,這看起來還算可以接受。但隨著步驟增加,程式碼很快就會演變成一個難以閱讀和維護的「俄羅斯娃娃」,形成巢狀呼叫地獄。
如果我們用程式碼來模擬製作抹茶蛋糕的過程,就會形成以下層層嵌套的程式:
const makeMatchaCake = (initialIngredients) =>
decorate(
chill(
assemble(
prepareMousse(
whipCream(
bakeSponge(initialIngredients)
)
)
)
)
);

圖 2 由內到外的巢狀呼叫結構(資料來源: 自行繪製)
這會引發幾個問題:
bakeSponge 開始,一路向外閱讀到 decorate 。這違背了我們平常理解線性流程的方式,增加認知負擔。assemble 和 chill 之間增加一個「添加水果夾層」的步驟。我們需要在密密麻麻的括號中找到正確的位置,小心翼翼地插入新的函數呼叫,並確保括號的配對依然正確。這種程式碼非常脆弱,任何小小的修改都可能導致語法錯誤、難以維護。console.log 來檢查中間步驟的產出是什麼。為了解決巢狀呼叫的可讀性問題,許多開發者可能會採用另一種策略:為每一步的結果創建一個臨時變數,這也是我平常比較會使用的方式 👀
const makeMatchaCake = (initialIngredients) => {
const bakedSponge = bakeSponge(initialIngredients);
const whippedCream = whipCream(bakedSponge);
const matchaMousse = prepareMousse(whippedCream);
const assembledCake = assemble(matchaMousse);
const chilledCake = chill(assembledCake);
const finalCake = decorate(chilledCake);
return finalCake;
};
這種寫法確實解決了閱讀順序的問題,我們現在可以由上而下地理解整個流程,符合我們一般的理解順序 👌。
然而,這也帶來了新的問題:
bakedSponge, whippedCream, matchaMousse... 這些變數絕大多數都只被使用一次,它們的存在只是為了將上一步的結果傳遞給下一步。這不僅增加了命名的負擔,也污染了函數的內部作用域。bakedSponge 是從 bakeSponge function 出來的,然後下一步會被丟到 whipCream function 內,這增加了心智模型的複雜度,尤其是在流程更長、變數更多的情況下。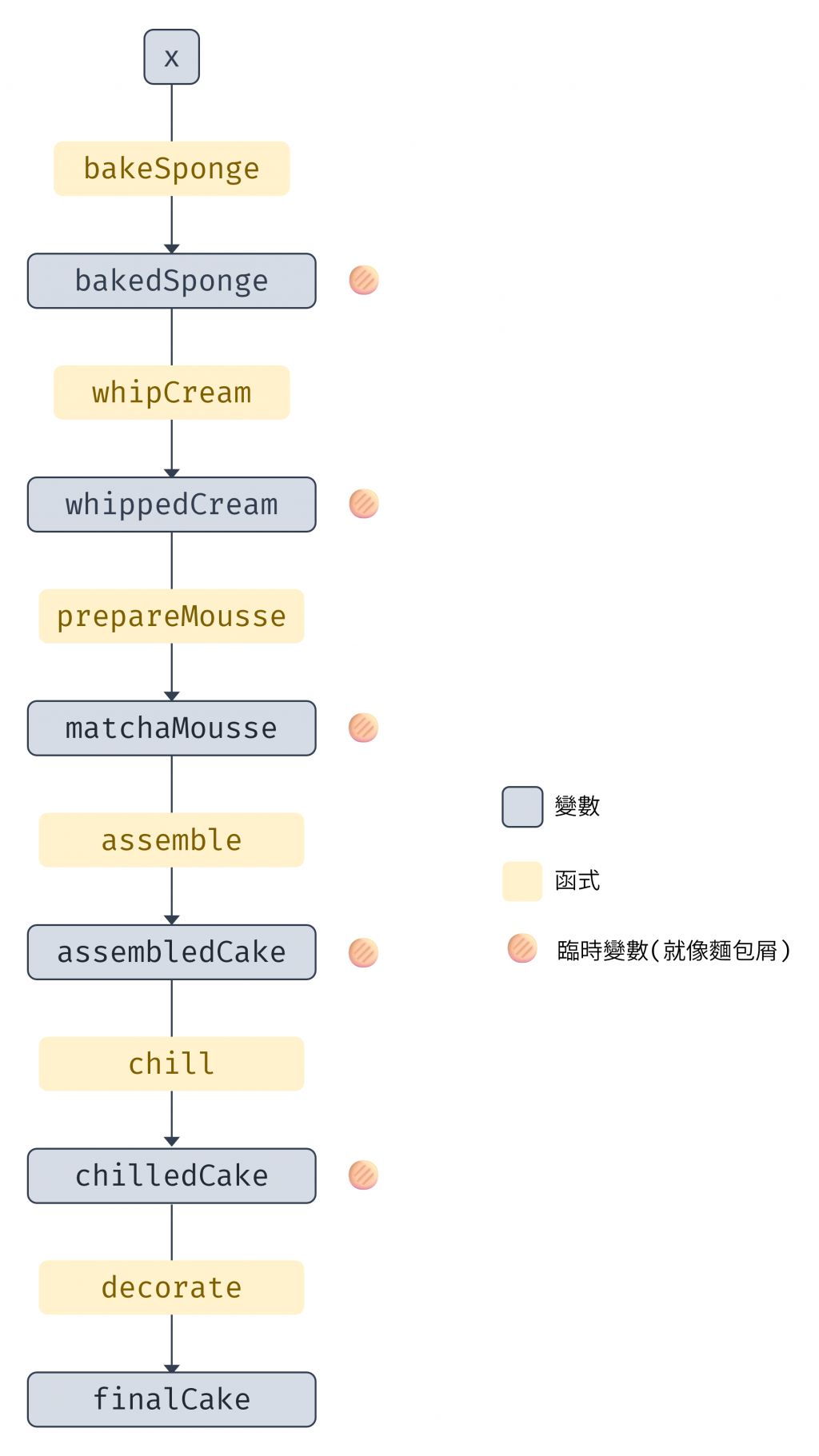
圖 3 充滿臨時變數的程式碼(資料來源: 自行繪製)
上面這兩種看似截然不同的寫法,其本質問題是相同的:它們都無法成功地將「一個接一個處理的序列」這個概念本身進行抽象。
巢狀呼叫把這個序列隱藏在語法結構的深處,而中間變數則把它拆解成一連串獨立但冗餘的指令。它們都在描述「如何」手動地把資料從一個函數傳遞到下一個,卻沒有一個簡潔、聲明式的方式來表達「資料將會流經這樣一個序列」這件事。
函數組合的出現,就是為了解決這問題,它讓我們不再關注於手動傳遞資料的細節,而是將整個處理「管道」本身,視為一個可以被創建、命名和重複使用的獨立實體。它將「描述瑣碎步驟」的思考方式轉換為「定義宏觀流程」的思維。
如果說巢狀呼叫和中間變數是代表著一個混亂的廚房——到處都是用了一次的碗盤(中間變數),或者試圖在一個巨大且不透明的攪拌盆裡完成所有工序(巢狀呼叫)——那麼函數組合就像是建立了一條高度自動化的食品生產線。
在這條生產線上,每一個工作站都是一個獨立、專注且可重複使用的機器(一個 Pure Function)。比如,「烘烤機」、「打發機」、「慕斯混合機」。而將這些機器無縫連接起來,讓半成品自動從一個站點流向下一個站點的,就是那條至關重要的「傳送帶」。
這條傳送帶,就是函數組合。
下圖簡單示意函數組合的傳送帶樣貌,這就像一個工廠生產線,前一個步驟的輸出會成為下一個步驟的輸入,中間不需要再儲存其他臨時變數。

圖 4 函數組合就像工廠傳送帶(資料來源: 自行繪製)
現在來看看使用函數組合後的程式碼會是什麼樣子:
// 假設我們有一個叫做 compose 的工具函數(等等會介紹 compose function 的實作細節)
const makeMatchaCake = compose(
decorate,
chill,
assemble,
prepareMousse,
whipCream,
bakeSponge
);
// 使用時,就像啟動整條生產線
const myCake = makeMatchaCake(initialIngredients);
這段程式碼帶來幾項優點:
makeMatchaCake 這個流程是由哪些步驟「組合」而成的。程式碼的意圖一目了然。compose 的執行順序是從右到左(從 bakeSponge 開始),但這種列表式的呈現方式遠比巢狀結構更容易理解和修改。makeMatchaCake 時,我們完全沒有提到它將要處理的資料 initialIngredients。這個參數(或稱之為 "point")被隱藏了。這種風格讓我們更專注於轉換流程本身,而不是被流經其中的具體資料所干擾。關於 Point-Free 在之後的文章會再說明,這裡先簡單這樣理解~通過函數組合 compose 工具函數,我們成功地將一個複雜的、多步驟的任務,抽象成了一條優雅的、可重用的資料處理管道。
我們已經通過「抹茶慕斯蛋糕製作生產線」感受到函數組合的力量,現在來看看它到底是什麼,以及如何實現它。
compose 與 pipe:資料流的方向函數組合的核心思想是將多個函數串連起來,形成一個新的函數。資料在這個串連的管道中流動,前一個函數的輸出成為後一個函數的輸入。這個流動是有方向性的,因此產生了兩種主要的組合工具:compose 和 pipe。
compose (組合):執行順序為 從右至左。這與數學上的函數組合定義 f(g(x)) 保持一致,先執行的函數 g 寫在右邊。pipe (管道):執行順序為 從左至右。這更符合我們閱讀的自然順序,也類似於 Unix/Linux 系統中的管道操作符 |,資料從左邊的命令流向右邊的命令。 兩者功能完全相同,唯一的區別就是函數參數的排列順序和執行方向。選擇哪一個純粹是個人或團隊的風格偏好。
用以下示意圖來釐清它們的資料流向:
圖 5 compose 和 pipe 的資料流向(資料來源: 自行繪製)
接著要介紹如何實現 compose 和 pipe function,要實現這兩個函式,我們可利用 JavaScript 陣列內建的 reduce 和 reduceRight 方法。
雖然前面文章介紹過 reduce,這裡還是稍微提一下 reduce 和 reduceRight~
reduce 與 reduceRight 的運作方式Array.prototype.reduce 和 Array.prototype.reduceRight 是 JavaScript 中內建的陣列方法,它們可以將陣列中的所有元素「歸納」或「縮減」成單一的輸出值。
它們的共同點是都需要傳入一個「回呼函數 (callback function)」和一個可選的「初始值 (initial value)」。回呼函數則會接收兩個主要參數:
accumulator (累加器):它儲存了上一次回呼函數執行的回傳值。在第一次執行時,如果提供了初始值,它就是初始值;如果沒有,它就是陣列的第一個元素。currentValue (當前值):陣列中正在被處理的當前元素。reduce 和 reduceRight 唯一的區別在於迭代方向 :
reduce:從陣列的最左邊 (索引 0) 開始,向右遍歷到陣列末尾。reduceRight:從陣列的最右邊 (最後一個元素) 開始,向左遍歷到陣列開頭。讓我們看一個簡單的例子來感受它們的差異:
const letters = ['a', 'b', 'c', 'd'];
// 使用 reduce (從左到右)
const leftToRight = letters.reduce((accumulator, currentValue) => accumulator + currentValue);
console.log(leftToRight); // 輸出: "abcd"
// 使用 reduceRight (從右到左)
const rightToLeft = letters.reduceRight((accumulator, currentValue) => accumulator + currentValue);
console.log(rightToLeft); // 輸出: "dcba"
上述舉例展示了它們處理順序的差異性。我們可以利用這個特性來實現 pipe 和 compose。
pipe 的實現 (使用 reduce)pipe 的目標是讓資料從左至右流經一系列函數。reduce 的執行方向完美契合這個需求。
const pipe = (...fns) => (x) =>
fns.reduce((v, f) => f(v), x);
以下來一步步拆解這段程式碼:
(...fns):這是一個剩餘參數語法,它會將所有傳入 pipe 的函數(例如 trim, toUpperCase)蒐集到一個名為 fns 的陣列中。=> (x) =>...:pipe 是一個高階函數,它回傳了另一個函數。這個回傳的函數接收一個參數 x,這就是我們整個管道的初始輸入值。fns.reduce(..., x):這是核心部分。這裡會對 fns 陣列執行 reduce。
reduce 會收到兩個參數
(v, f) => f(v),這裡面的:
v 是累加器,代表上一個步驟的結果,可以理解成上一個步驟的函式執行結果。f 是當前值,代表 fns 陣列中目前要執行的函數。f(v) 的意思是「執行當前的函數 f,並將上一步的結果 v 作為其參數」。這個執行的結果,會自動成為下一次迭代的 v。x,是 reduce 的初始值。這代表在第一次迭代時,累加器 (v) 的值就是我們傳入的 x。舉例來說,pipe(fn1, fn2, fn3)(initialValue) 的整個流程就像這樣:
reduce 開始,v 的初始值是 initialValue。f 是 fn1。執行 fn1(initialValue),回傳 result1。v 現在是 result1,f 是 fn2。執行 fn2(result1),回傳 result2。v 現在是 result2,f 是 fn3。執行 fn3(result2),回傳 finalResult。reduce 結束,回傳 finalResult。compose 的實現 (使用 reduceRight)理解了 pipe 後,compose 可能就好理解一點。compose 的目標是從右至左執行,這正是 reduceRight 會做的事。事實上,在 MDN 的文件中也提到了 reduceRight 的一個經典用途就是Defining composable functions。
const compose = (...fns) => (x) =>
fns.reduceRight((v, f) => f(v), x);
這段程式碼的邏輯與 pipe 相同,唯一的區別就是將 reduce 換成了 reduceRight。reduceRight 會從 fns 陣列的最後一個函數開始執行,並一路向左處理,完美地模擬了 f(g(h(x))) 先執行 h、再執行 g、再執行 f 的執行順序。
下表整理了兩者差異:
| 工具 | 實作方式 | 執行順序 | 類比 |
|---|---|---|---|
compose |
(...fns) => x => fns.reduceRight((v, f) => f(v), x) |
從右至左 | 數學定義 f(g(x)) |
pipe |
(...fns) => x => fns.reduce((v, f) => f(v), x) |
從左至右 | Shell 指令 cmd1 | cmd2 |
另外補充,雖然這裡介紹了 compose 和 pipe function 的實作,但實際應用時仍建議參考第三方 library,例如 Ramda - compose、lodash 等。
在上一篇文章中,我們提到 Currying (柯里化)。而其實 Currying 與函數組合(Composition)並不是獨立的概念,他們的結合可展現 Functional Programming 的潛力。
現在有個問題是,我們上面實現的 compose 和 pipe 工具,都隱含了一個假設——管道中的每一個函數都只接受一個參數,因為前一個函數只會回傳一個值,這個值將被直接傳遞給下一個函數,下一個函數也因此只接受一個參數。
但現實世界中的函數並非總是如此。如果我們想在管道中使用一個需要多個參數的函數,例如 add(a, b),會發生什麼事?
const add = (a, b) => a + b;
const multiplyByTwo = (x) => x * 2;
// 嘗試組合一個需要兩個參數的函數
const calculate = pipe(
add(5), // 這裡會立即執行 add(5, undefined),回傳 NaN,這個回傳值無法作為 function 被呼叫執行
multiplyByTwo
);
// 這將會導致錯誤,會跳出 f is not a function 的錯誤,因為 add(5) 的回傳值不是 function
// calculate(10);
這段程式碼會失敗,因為 add(5) 並沒有像我們期望的那樣回傳一個「等待另一個數字的函數」,而是立即計算 5 + undefined,結果是 NaN。整個 pipe 管道在第一步就崩潰了。
這就是 Currying 派上用場的地方。Currying 的核心作用就是將一個接受多個參數的函數,轉換成一連串只接受單一參數的函數鏈 。它就像一個「轉接頭」,可以讓任何形狀(參數個數)的「插頭」(函數)都能符合我們管道所要求的「單孔插座」。
讓我們用 Currying 來改造 add 函數:
// 一個柯里化版本的 add 函數
const curriedAdd = (a) => (b) => a + b;
const multiplyByTwo = (x) => x * 2;
// 現在,我們可以預先配置 add 函數
const addFive = curriedAdd(5); // 這一步回傳的是一個新函數:(b) => 5 + b
// 現在的組合就完全合法且有效了 ✅
const calculate = pipe(
addFive,
multiplyByTwo
);
// 執行 pipe
const result = calculate(10); // 流程: 10 -> addFive(10) -> 15 -> multiplyByTwo(15) -> 30
console.log(result); // 輸出: 30
通過 Currying,我們將 add 函數進行了「部分應用 (Partial Application)」,創建了一個專門化的新函數 addFive。這個新函數的「形狀」是 (b) => a + b,完美地契合了組合管道對單一參數函數的要求。
可以說,Composition 提供了資料流的「結構」(管道本身),而 Currying 則提供了靈活的「接口」(將任意函數適配到管道中)。Currying 是讓通用化、可重用的函數組合成為可能的關鍵技術。它賦予我們一種能力,可以預先配置和客製化我們的工具函數,然後像樂高積木一樣,將它們輕鬆地拼接到任何處理流程中。
函數組合不只是讓程式碼變整潔,它其實延續了我們早就熟悉的數學直覺:結合律。
在數學裡,有些運算不管怎麼「分組」,結果都一樣(只要順序不變)。
這個特性讓我們在計算時很安心,因為分組方式不會影響答案。
將這個想法搬到程式,就是函數組合的結合律:當你把三個以上的函數串起來時,你如何對它們進行「分組」是不重要的,只要它們的「順序」保持不變即可。
換句話說,對 f(g(h(x))) 這樣的組合,無論是先將 g 和 h 看作一個整體,再與 f 組合;還是先將 f 和 g 看作一個整體,再與 h 組合,最終的結果都是完全相同的。
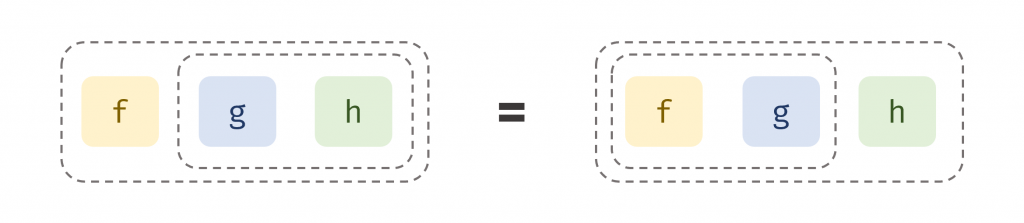
圖 6 結合律示意圖(資料來源: 自行繪製)
在程式碼中,這代表 compose(f, compose(g, h)) 和 compose(compose(f, g), h) 是等價的,也和 compose(f, g, h)是等價的。

圖 7 結合律在 compose 的應用(資料來源: 自行繪製)
可用程式來驗證這一點:
const f = (str) => `${str}!`;
const g = (str) => str.toUpperCase();
const h = (str) => str.trim();
// 方式一:先組合 g 和 h
const pipeline1 = compose(f, compose(g, h));
// 方式二:先組合 f 和 g
const pipeline2 = compose(compose(f, g), h);
// 方式三:不分組,直接組合
const pipeline3 = compose(f, g, h);
const input = ' hello world ';
console.log(pipeline1(input)); // "HELLO WORLD!"
console.log(pipeline2(input)); // "HELLO WORLD!"
console.log(pipeline3(input)); // "HELLO WORLD!"
上面的程式結果證明,無論我們如何分組,最終的行為都是一致的。
這看起來可能只是一個有趣的數學特性,但它在軟體工程中的意義是巨大的。結合律賦予了我們可以隨意且安全地對程式碼進行重構和抽象的超能力。
假設在一個大型應用中,我們有一條非常長的處理管道:
const processUserData = compose(
generateReport,
saveToDatabase,
formatAddress,
capitalizeName,
validateEmail,
trimWhitespace
);
我們發現 capitalizeName、validateEmail 和 trimWhitespace 這幾個步驟經常一起出現,它們會構成一個「處理使用者輸入」的子流程。由於函數組合滿足結合律,我們可以充滿信心地將這幾個相鄰的函數提取出來,組合成一個新的、可重用的函數,而完全不必擔心會破壞原有的邏輯。
// 提取出一個可重用的子流程
const purifyUserInput = compose(
capitalizeName,
validateEmail,
trimWhitespace
);
// 用新的抽象來重構原有的管道
const processUserData = compose(
generateReport,
saveToDatabase,
formatAddress,
purifyUserInput // <-- 使用新的、更高級別的抽象
);
結合律是數學上的保證,它確保了我們的抽象是「無洩漏」的。這代表我們可以從最小、最簡單的純函數開始,逐步將它們組合成更複雜、更具業務意義的函數,然後再將這些函數進一步組合,最終構建出整個應用程式。
這個過程中的每一步都是安全、可靠且可預測的。這正是函數組合能成為管理軟體複雜度的可擴展技術的根本原因。
雖然函數組合帶來了聲明式的優雅,但它也可能帶來一個挑戰:當一條長長的管道最終產出的結果不符合預期時,問題是出在哪個環節呢?由於中間值被隱藏在管道內部,整個流程看起來就像一個「黑盒子」,讓除錯變得困難。
那要如何解決呢? 我們需要的不是傳統的斷點 debugger,而是一個可以被安裝在「水管」任意位置的「透明觀察窗」。通常稱這個工具為 trace 或 tap。
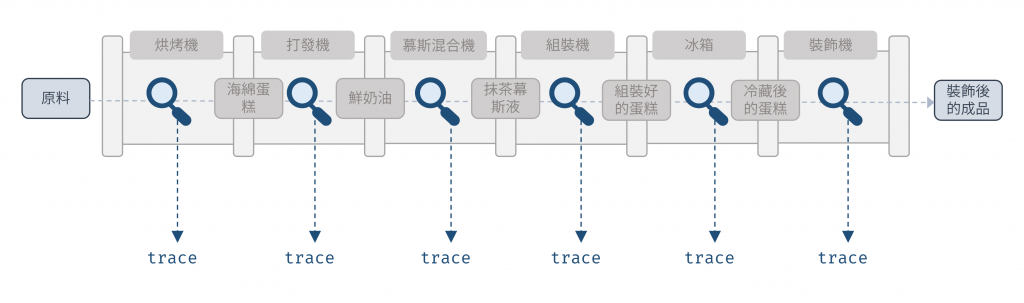
圖 8 trace 就像管道中的透明觀察窗(資料來源: 自行繪製)
這個 trace 函數是一個高階函數,它的作用是:接收一個值,對這個值執行一個副作用(例如 console.log),然後原封不動地將這個值回傳,確保資料流不會被中斷。
我們可以這樣實現一個簡潔的 trace 工具:
// label 參數讓我們可以標記這是管道的哪一個位置
// (console.log(...), x) 利用了逗號運算符:
// 它會先執行左邊的表達式(console 輸出),然後回傳右邊表達式的值(原始值 x)
const trace = (label) => (x) => (console.log(`${label}:`, x), x);
如果我們懷疑 compose 的函數中間有問題時,就可以像安裝水龍頭一樣,在任意兩個函數之間插入 trace 函數來觀察流經此處的資料。
讓我們回到製作抹茶蛋糕的例子,假設我們發現最終的蛋糕口感不對,我們懷疑是在慕斯製作或冷藏環節出了問題。我們可以這樣除錯:
const makeMatchaCake = compose(
decorate,
trace('步驟 5 -> 裝飾後'), // 觀察最終成品
chill,
trace('步驟 4 -> 冷藏後'), // 觀察冷藏效果
assemble,
trace('步驟 3 -> 組裝後'), // 觀察組裝狀態
prepareMousse,
trace('步驟 2 -> 慕斯製作後'), // 觀察慕斯液狀態
whipCream,
trace('步驟 1 -> 奶油打發後'), // 觀察奶油狀態
bakeSponge
);
makeMatchaCake(initialIngredients);
執行這段程式碼後,console 會印出每一步的輸出結果:
// 步驟 1 -> 奶油打發後: {...whippedCreamObject }
// 步驟 2 -> 慕斯製作後: {...mousseObject }
// 步驟 3 -> 組裝後: {...assembledCakeObject }
// 步驟 4 -> 冷藏後: {...chilledCakeObject }
// 步驟 5 -> 裝飾後: {...finalCakeObject }
我們可透過 console 印出的內容來精確地定位到是哪一個環節的輸出與預期不符,快速找到問題的根源。
函數組合的思維不只存在於「資料處理」這種抽象範例,它其實也和前端框架有關。
以 React 為例,一個 component function 就是 props -> ReactElement 的純函數。這段程式碼不是立刻操作真實 DOM,而是回傳一份 UI 的描述。React 再負責把這些描述「組裝」起來,渲染成真實的畫面。
小函數可透過 pipe 或 compose 串起來,形成一條更大的處理管線;在 React 裡,不同的 component function 也可以透過「嵌套」與「組合」串起來,構成更複雜的畫面。
const Layout = ({ children }) => <div className="layout">{children}</div>;
const Toolbar = ({ children }) => <div className="toolbar">{children}</div>;
const UserName = ({ user }) => <span>{user.name}</span>;
const Page = ({ user }) => (
<Layout>
<Toolbar>
<UserName user={user} />
</Toolbar>
</Layout>
);
這裡的 Page 就像一條被組合起來的「UI 管線」:從 UserName 處理最小的顯示單元,到 Toolbar 再到 Layout,最後組成完整的畫面。
component function 本身就像一個可重用的小步驟,而巢狀組合就是 UI 世界的函數組合。
以下透過三個問題來總結函數組合。
為了解決多步驟資料處理流程中的混亂。當我們需要將一個值的處理結果傳遞給下一個步驟時,傳統寫法會導致難以閱讀的「巢狀呼叫地獄」,或是充滿臨時變數、冗長且難以維護的程式碼。
processData = pipe(stepA, stepB, stepC)。連接的細節被自動化處理,讓程式碼變得簡潔、直觀且易於重構。它是一種將多個小而專一的函數串連起來,創建一個全新、更強大函數的技術。其核心是建立一條「資料處理管道」,前一個函數的輸出會自動成為下一個函數的輸入。透過 pipe (由左至右) 或 compose (由右至左) 等工具,我們可以像組合樂高積木一樣,從可重用的零件建構出複雜的邏輯流程。
