Day22 | Rosalind 生資解題 - 012. GRPH（Overlap Graphs） - 上篇

題目連結：https://rosalind.info/problems/grph/

直接來看輸入與輸出

輸入

>Rosalind_0498
AAATAAA
>Rosalind_2391
AAATTTT
>Rosalind_2323
TTTTCCC
>Rosalind_0442
AAATCCC
>Rosalind_5013
GGGTGGG

輸出

Rosalind_0498 Rosalind_2391
Rosalind_0498 Rosalind_0442
Rosalind_2391 Rosalind_2323

這一題是重疊圖，其中提到O3，等於overlop 3個元素（長度k=3）
就是指，「1號序列的前三碼，若與2號序列的末三碼一樣」，則將其標示出來
可返回任意排序內容

重疊？混淆點釐清

直觀一點的話，想像有鋸齒狀卡住的結構，一股力量往左扯、下面一股力往右扯

上面有三個元素、下面也三個元素

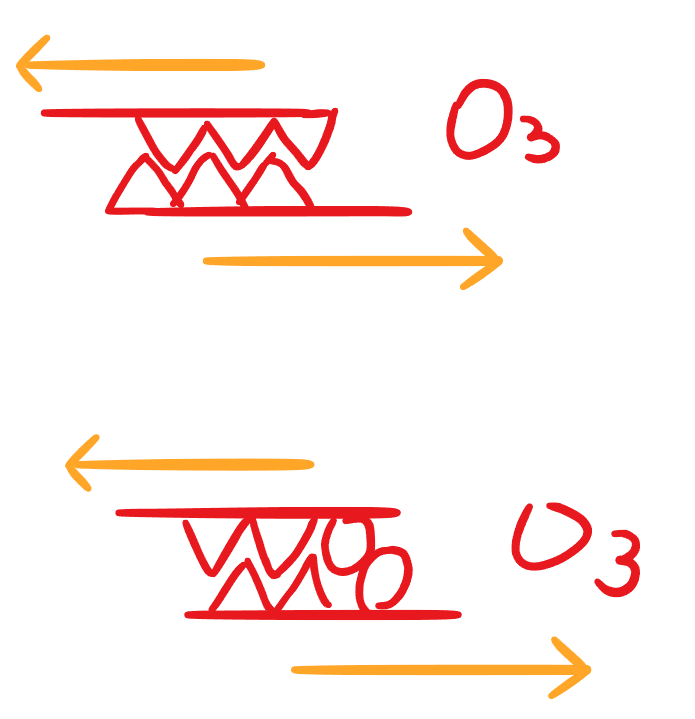
O3關係就是有三個元素，上下互相卡的很緊
卡越緊代表重疊度很高、很overlap（不是"很ｏｖｅｒ"，是overlap）

那麼再看這張圖，上下元素數量來到四個

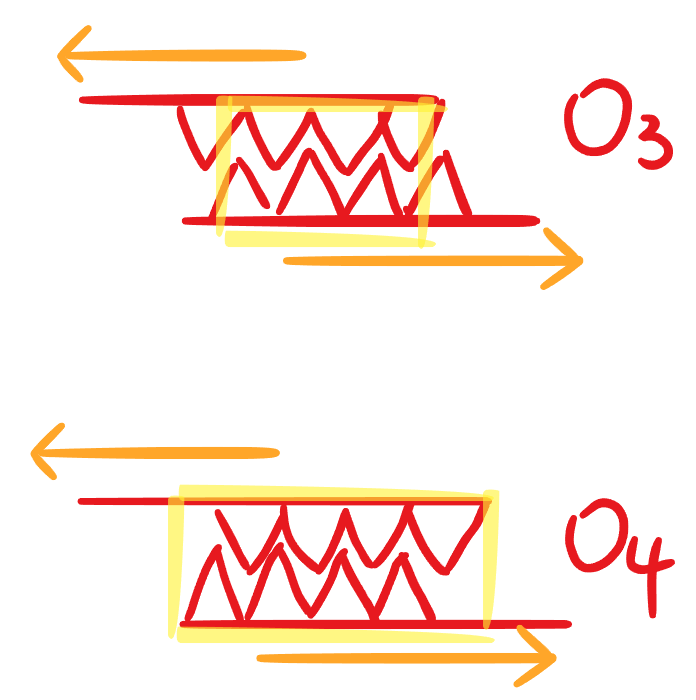
可以形成O3關係、也可以形成O4關係
O4的話卡死更緊了呢，代表更overlap了

結論：
AAACTTT與CTTTCCC => 不是O3關係，而是O4關係，因為重複了CTTT

AAATTTT與TTTTCCC => 是O4關係，重複了TTTT
但他們同時也可以形成O3關係TTT、O2關係TT、O1關係T

在圖論或組裝實作中通常只記「最大重疊」，以避免歧義與重複邊。但在這一題中只考慮O3邊，所以也需將O3關係列入計算

但是要小心
適用於O4（長）關係的，則不一定適用於O3（短）關係
反之，不適用於O3（短）關係的，不代表一定無法形成O4（長）關係
要看兩者的重複結構關係

解法一：暴力破解

O(n²) 的解法，直接把A與B兩兩配對，將每一個組合全部列出比對
符合O3關係的就抓出來！

程式碼：

data = """
>Rosalind_0498
AAATAAA
>Rosalind_2391
AAATTTT
>Rosalind_2323
TTTTCCC
>Rosalind_0442
AAATCCC
>Rosalind_5013
GGGTGGG
"""

def parse_fasta(data: str) -> dict:
	sequences = {}
	label = ""
	for line in data.strip().splitlines():
		line = line.strip()  # 縮排防呆
		if not line:  # 跳過空行
			continue
		if line.startswith(">"):
			label = line[1:].strip()  # 去除label頭尾空白
			if not label:  # 跳過空標籤（不合法）
				label = ""
				continue
			sequences[label] = ""
		elif label:
			sequences[label] += line

	return sequences


seqs = parse_fasta(data)
for s1 in seqs:
	for s2 in seqs:
		if s1 == s2:
			continue
		if seqs[s1][-3:] == seqs[s2][:3]:
			print(s1, s2)

補充生物知識點

這一題雖然是在建 Overlap Graph 重疊圖運算，只是在計算前後是否相等，但其實更像在做「拼圖的組裝」，將每一塊拼圖以合理的方式拼建起來。

類似次世代定序（NGS）將多個小片段，依照最有可能的組合方式拼起來，將拼每一個Reads（NGS產生的短片段序列）拼裝出原本一整條基因的樣貌

次世代定序 (NGS) 的組裝流程：
因為技術上，仍無法一次直接讀完整條基因體
而且目前技術讀的時候，無法做到100%精確

第二代定序（NGS）短讀長，市占率最高
第三代定序（TGS）長讀長，至今仍然在發展，尚未完全成熟和普及

坦白說，所以我們這一題O₃ overlap graph 每個read兩兩比對的解法
只適合小資料驗證概念，因為用在NGS的話，運算量會非常可觀（幾百萬甚至幾億條reads），運算時間非常嚇人

給個數字對比：

次世代定序 (NGS, Next-Generation Sequencing)：

一次只能讀大約數百個以下的bp

• Illumina公司的SBS（Sequencing by Synthesis）：準確度極高，但讀長短，需大量拼接。讀長50–200bp，再繼續往下讀精確度大幅降低（訊號誤差會放大累積）

• SOLiD (Applied Biosystems / Life Technologies / 被Thermo Fisher收購)：ligation探針，讀長35–75bp，已被市場淘汰

• Ion Torrent (被Thermo Fisher收購)：半導體晶片定序，偵測H⁺釋放，讀長100–400bp，已被市場淘汰

第三代定序 (TGS, Third-Generation Sequencing)：

一次能讀非常長的bp，但仍需克服精準度問題

• PacBio公司的SMRT：利用零模波導 (Zero-Mode Waveguide, ZMW)，觀測單一聚合酶合成DNA過程，讀長可達10000-100000bp，HiFi Reads大幅提升準確度

• Oxford Nanopore公司的Nanopore：讓DNA分子通過奈米孔，偵測電流阻抗變化以辨識核苷酸，讀長可達數十萬甚至幾乎無上限

基因體長度（genome）：
人類基因體大約30億個鹼基對(bps)，DNA拉直大約能達1公尺長

所以做基因定序時，會將同一份基因體（Genome）拷貝許多次之後、打碎再讀取
之後再盡可能讀取

目前定序魔王在於：
同聚物序列（AAAAA…）難以判讀，因為電流訊號太相似，難以準確判斷「到底是5個A，還是7個A」，而目前市面上存活的這些技術都能部分克服、或者繞過這個難題，以達到精準

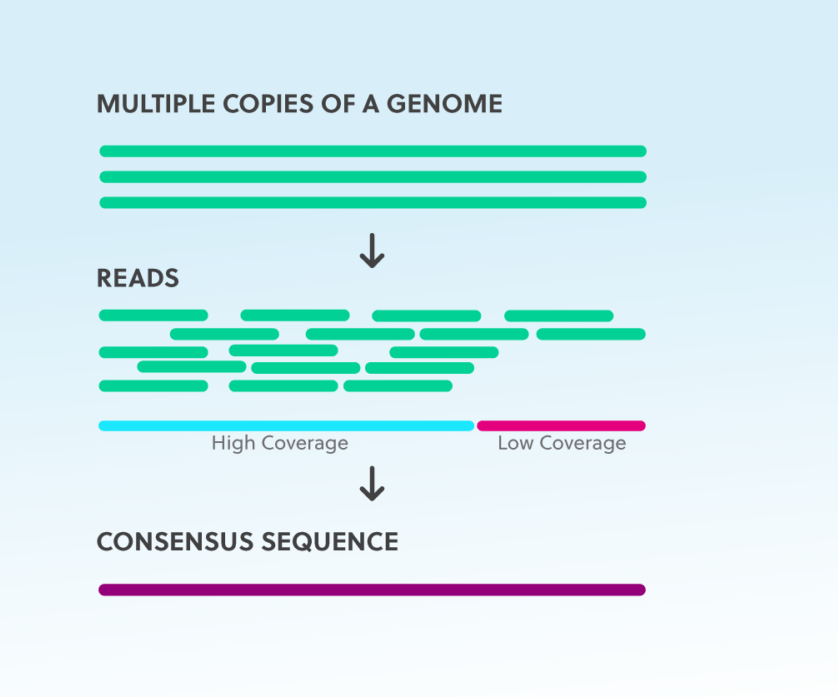
看圖可以發現，我們無法完全把每個copy（複本）上的所有序列都讀過一遍，因為打碎之後還要蒐集全部碎片是不務實的
只能做到盡量cover，反正只要copy的數量充足，定序時讀取足夠多次
以概率來說，就能夠cover整條genome

所以在實驗設計時會要求coverage數值，以降低誤差
30X coverage => 每個鹼基平均會被讀到30次
100X coverage => 每個鹼基平均會被讀到100次
即使個別read有可能錯，只要覆蓋率夠高就能夠平均、抵銷掉誤差

單位釐清：bp vs nt？

單位到底是用「bps還是nts」

bp (base pair)：雙股 DNA 的長度單位。
nt (nucleotide)：單股核酸（單股DNA或RNA）的長度單位

兩者都是在指序列的長度
嚴格來說，1bp = 2nts，因為一個「鹼基配對」是由「2個核甘酸互補」組成

由於至今所有的定序方式都是讀取「單股」辨識，沒辦法讀雙股黏在一起的序列
就有點像，讀書總要把書本攤開、分離成左右兩個頁面，才能讀取上面的文字
雖然定序機器讀的都是單股，但要寫nt還是bp取決於樣本最終是RNA還是DNA

RNA定序（讀的是RNA）就寫nt，DNA定序（讀的是雙股DNA）就寫bp
...嚴格來說，理應如此啦！
但是至今不論DNA或RNA，用的「普遍都是bp」

就像服飾店講「一條拉鍊」，沒有人糾正「應該是一對齒鏈」

去服飾店裡問，阿姨您今天修理了幾條拉鏈？
老闆娘馬上就回答你了
通常老闆娘不會反問：「你到底是問幾對拉鍊、還是幾條拉鏈？」

但其實一條拉鍊是由兩排齒鏈互相咬合，嚴格來說應該是一對，由兩條鏈帶組成

PS 拉鏈是1917年Gideon Sundbäck的專利