Day21 | Rosalind 生資解題 - 011. FIBD（Mortal Fibonacci Rabbits）限制壽命版 - 下篇

延續前一篇

補充數學芝士

接下來要補充一點，營養的
今天要集中專注度，補充數學精神！

生兔規則

前面使用的是「生兔規則」：

m=2 => Fn = F(n-2)
m=3 => Fn = F(n-2) + F(n-3)
m=4 => Fn = F(n-2) + F(n-3) + F(n-4)
任意m => Fn = F(n-2) + F(n-3) + F(n-4) + F(n-5) ... + F(n-m)

直觀理解：
當輪兔總數 = Σ（前 m-1 輪活兔會生的新兔）
這個算法，死亡兔自動被扣掉（死亡兔在死的那瞬間生出新兔，剛好取代抵消）

當m=2 => 兔子只活2輪。死亡數剛好等於出生數，每一回合都只有一隻兔子
當m趨近無窮大 => 退化成經典費氏數列：F(n-1) + F(n-2)

生兔規則考量點：
哪些兔子有繁殖能力？（滿 2 輪以上的兔子會繁殖一次）
每對兔子每輪生多少對？（1 對還是多對？）
=> 逐輪加總活著的貢獻

接下來，將「生兔規則」整理成更泛用的「各輪生死規則」

各輪生死規則

把「各輪生死規則」抽象成通用的數學公式

直觀理解：
此輪兔數 = 上一輪基數 + 新生數 - 死亡數
Fn = F(n-1) + F(n-2) - F(n-m-1)
這回合兔子數 = 上個月成熟兔總數 + 上個月幼兔 - 死亡數（死掉的是 n-m-1月 出生的那一批兔）

m=2 => Fn = F(n-1) + F(n-2) - F(n-3)
m=3 => Fn = F(n-1) + F(n-2) - F(n-4)
m=4 => Fn = F(n-1) + F(n-2) - F(n-5)
任意m => Fn = F(n-1) + F(n-2) - F(n-m-1)

當m=2 => Fn = F(n-1)。每一回合都上一輪留下的活兔。因為F(n-2)與F(n-3)，要馬兩者都為1，要馬就都為0。本輪新生的兔子 - 本輪剛好死掉的兔子=0。
當m趨近無窮大，F(n-m-1)趨近於0（死亡數可忽略）

上一輪留下的活兔+本輪新生的兔子+本輪剛好死掉的兔子

各輪生死規則考量點：
每隻兔子能活幾輪？（固定的時間壽命）
死掉的兔子，會不會影響新兔的數量？（死亡是在「繁殖後」還是「繁殖前」發生）
=> 從累積總數扣掉死亡者

兩者描述不同，但其實是等價的
如何證明「生兔規則」等價於「各輪生死規則」？

遞迴關係式

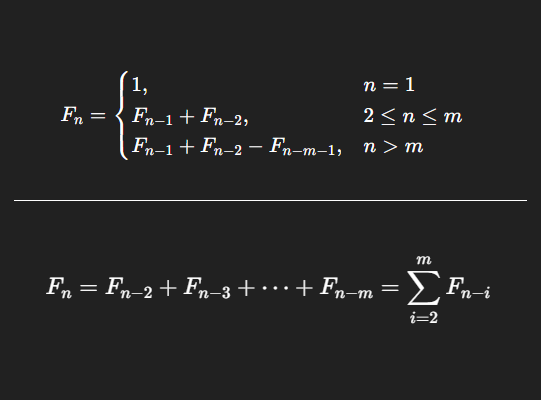
此處假設兔子壽命3個月，m=3

F(n) = F(n-1) + F(n-2) - F(n-4) = F(n-2) + F(n-3)

推導過程如下

方法1：無窮代換法

F(n-1) + F(n-2) - F(n-4)
= [F(n-2) + F(n-3) - F(n-5)] +F(n-2) - F(n-4)
= F(n-2) + F(n-2) + F(n-3) - F(n-4) - F(n-5)
= F(n-2) + [F(n-3) + F(n-4) - F(n-6)] + F(n-3) - F(n-4) - F(n-5)
= F(n-2) + F(n-3) + F(n-3) - F(n-5) - F(n-6)
= F(n-2) + F(n-3) + [F(n-4) + F(n-5) - F(n-7)] - F(n-5) - F(n-6)
= F(n-2) + F(n-3) + F(n-4) - F(n-6) - F(n-7)
= F(n-2) + F(n-3) + [F(n-5) + F(n-6) - F(n-8)] - F(n-6) - F(n-7)
= F(n-2) + F(n-3) + F(n-5) - F(n-7) - F(n-8)
= ...
（無窮代換下去，後三項會趨近一個常數、收斂，用近似常數C表示）
= F(n-2) + F(n-3) + C

上述推導對任意壽命m的兔子皆成立

方法2：特徵根法

假設解的型態 Fₙ = rⁿ，代入：

F(n) = F(n-1) + F(n-2) - F(n-4) <=> rⁿ = rⁿ⁻¹ + rⁿ⁻² − rⁿ⁻⁴

rⁿ = rⁿ⁻¹ + rⁿ⁻² − rⁿ⁻⁴
(同除rⁿ⁻⁴)
=> r⁴ = r³ + r² − 1
=> r⁴ − r³ − r² + 1 = 0
=> (r − 1)(r³ − r − 1) = 0
=> (r − 1) = 0 or (r³ − r − 1) = 0

最後，取 r³ − r − 1 = 0
=> r³ = r + 1
(同乘rⁿ⁻³)
=> rⁿ = rⁿ⁻² + rⁿ⁻³ <=> F(n) = F(n-2) + F(n-3)

上述推導對任意壽命m的兔子皆成立

對照以下（左側公式），我們可以再寫出一種遞迴解法

m=2 => F(n-1) + F(n-2) - F(n-3) <=> F(n-2)
m=3 => F(n-1) + F(n-2) - F(n-4) <=> F(n-2) + F(n-3)
m=4 => F(n-1) + F(n-2) - F(n-5) <=> F(n-2) + F(n-3) + F(n-4)
...

解法三（遞迴補充）

（前一篇文章提到另外兩種解法）

def mortal_fib_recur(n: int, m: int) -> int:
    # 尚未進入回合
    if n <= 0:
        return 0

    # 前兩回合都只有1隻兔子
    if n == 1 or n == 2:
        return 1

    # 還沒有死亡時（從3..m月），等同於經典 Fibonacci
    if n <= m:
        return mortal_fib_recur(n - 1, m) + mortal_fib_recur(n - 2, m)

    # 第一次有兔子死掉（首次死亡月）：m+1月，只扣掉最初那1對
    if n == m + 1:
        return mortal_fib_recur(n - 1, m) + mortal_fib_recur(n - 2, m) - 1

    # 後續死亡月：n > m+1（扣掉 n-m-1 月出生的那批兔子）
    return (mortal_fib_recur(n - 1, m) + mortal_fib_recur(n - 2, m) - mortal_fib_recur(n - m - 1, m))


print(mortal_fib_recur(6, 3))  # 4