Day24 | Rosalind 生資解題 - 013. IEV（Calculating Expected Offspring） + numpy dtype

今天這題很快！
一下就下課囉

題目連結：https://rosalind.info/problems/iev/

輸入：

1 0 0 1 0 1

輸出：

3.5

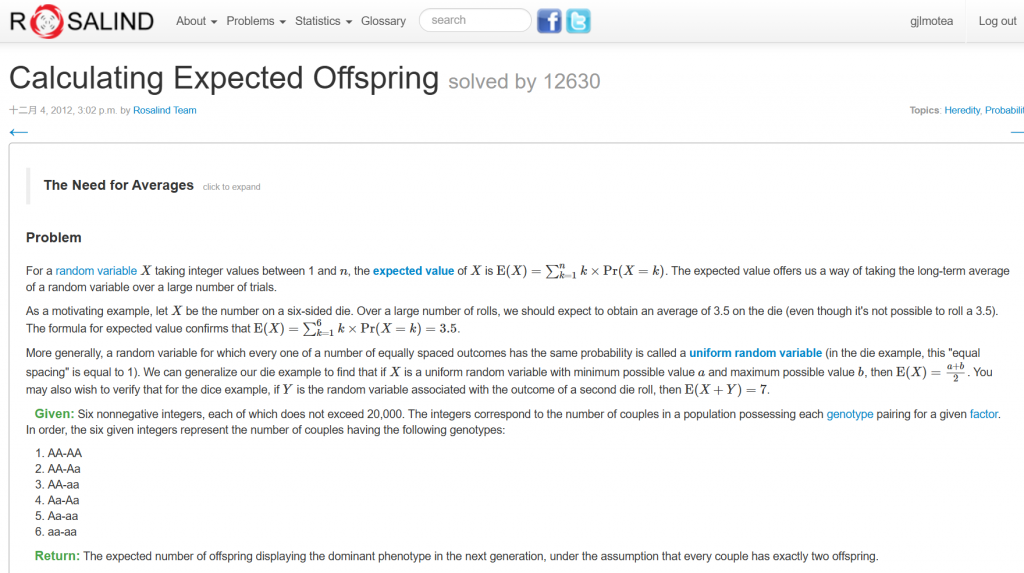
計算子代的顯性性狀數量！

所以拿到資料第一步驟，將一連串的字串切割，轉成數字以陣列存放
再運用龐尼特方格，直接將每一種配對 顯性機率的期望值計算出來，作為權重

基因型配對的權重：
AA-AA：1（怎麼生都是顯性）
AA-Aa：1（怎麼生都是顯性）
AA-aa：1（怎麼生都是顯性）
Aa-Aa：0.75
Aa-aa：0.5
aa-aa：0（怎麼生都是隱性）

最後將數字乘上權重，再乘上子代數量即可

程式碼：

data = "1 0 0 1 0 1"
counts = [int(x) for x in data.split(" ") if x.isdigit()]
weight = [1, 1, 1, 3 / 4, 1 / 2, 0]
offspring = 2

result = [d * w for d, w in zip(counts, weight)]
print(sum(result)*offspring)

寫成function
可以再加做一個陣列長度的檢查

def expected_offspring(raw_data: str, offspring: int = 2) -> float:
    weight = [1, 1, 1, 0.75, 0.5, 0]
    counts = [int(x) for x in raw_data.split() if x.isdigit()]

    if len(counts) != len(weight):
        raise ValueError(f"資料長度不符: data={len(counts)}, weight={len(weight)}")
    if any(d < 0 for d in counts):
        raise ValueError("輸入的配對數不可為負數")

    return offspring * sum(d * w for d, w in zip(counts, weight))

print(expected_offspring("1 0 0 1 0 1"))

用numpy的解法

透過簡單題目，矩陣運算來加減練習numpy的使用方法

初始化陣列時，可以不指定dtype，因為numPy會自動推斷
如果若有混合型別（ex: int + float），numpy會自動轉成「能容納全部資料的最高型別」

型別升階邏輯 type promotion hierarchy：
bool → integer → floating → complex → string → object
（complex 是 複數 = 實部+虛部）

但是建議在開發時，
如果能夠確定型別就自己寫、明確指定dtype，可以避免未來推斷錯誤

import numpy as np

raw_data = "1 0 0 1 0 1"

# counts = np.fromstring(raw_data, sep=' ', dtype=int) # 指定dtype寫法
counts = np.fromstring(raw_data, sep=' ')

weights = np.array([1, 1, 1, 0.75, 0.5, 0])
# weights = np.array([1, 1, 1, 0.75, 0.5, 0], dtype=float) # 指定dtype寫法

offspring = 2

expected = offspring * counts.dot(weights)  # = 2 * Σ(counts_i * weights_i)

print(expected)

改寫成function

import numpy as np

def expected_offspring(raw_data: str, offspring: int = 2) -> float:
    counts = np.fromstring(raw_data, sep=' ', dtype=int)
    weights = np.array([1, 1, 1, 0.75, 0.5, 0], dtype=float)

    if counts.size != weights.size:
        raise ValueError(f"資料長度不符: counts={counts.size}, weights={weights.size}")

    if (counts < 0).any():
        raise ValueError("輸入的配對數不可為負數")

    return float(offspring * counts.dot(weights))

print(expected_offspring("1 0 0 1 0 1"))

numpy題外話

(counts < 0).any()
與
any(x < 0 for x in counts)

雖然都是做一樣的事情（迭代迴圈）
但一個是給py迴圈（上者）用Python在一個一個元素上比對，逐項
一個是給更快的C做迴圈（下者）NumPy在C底層一次性批次運算，向量化

早期Python沒有內建任何矩陣或向量功能。
資料科學家、軟體工程師如果要做矩陣運算
只能用以下寫法

for i in range(n):
    for j in range(n):
        c[i][j] = a[i][j] + b[i][j]

Python每個元素都要型別檢查、函式呼叫，開銷極大

後來有人目標想讓Python有MATLAB那樣的矩陣
在 C 語言中寫了一套底層實作，讓Python只負責呼叫介面。
NumPy在C層一次批次處理整塊連續記憶體，開銷極小
兩者速率大概相差20-200倍，取決於資料量