iT邦幫忙

2025 iThome 鐵人賽
DAY 24
0
Rust

用刷題來練RUST系列 第 24 篇

用刷題來練RUST Day24 Inorder Traversal & Preorder Traversal

17th鐵人賽
67 瀏覽

  • 分享至 

  • xImage
    •  

在Day23介紹了後序遍歷(Postorder Traversal)，接這介紹剩下兩個遍歷，三種差別只在於 root 出現的時間點。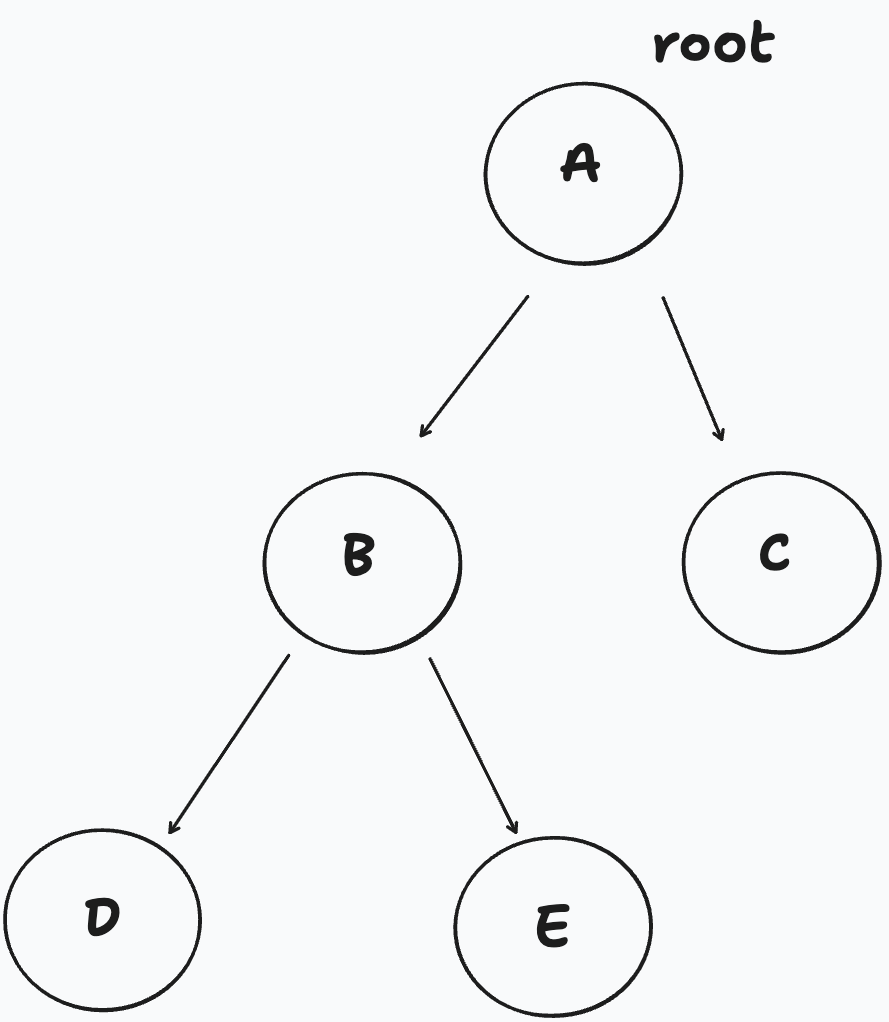
https://ithelp.ithome.com.tw/upload/images/20251006/201422058a7bShlSdl.png

前序遍歷 Preorder Traversal

先訪問 root，再訪問左子樹，最後訪問右子樹，如圖走的順序A→B→D→E→C

主要用途：

  1. 序列化樹

    Leetcode 144. Binary Tree Preorder Traversal

    題目：給一顆樹依照preorder順序將節點的值插入陣列回傳

    輸入：root = [1,null,2,3]

    輸出 : [1,2,3]

    解法：依照preorder走法將節點的值存到陣列回傳

    
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn preorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
        let mut ans:Vec<i32> = Vec::new();
        Self::get_vec(root,&mut ans);
        ans

    }

    pub fn get_vec(root: Option<Rc<RefCell<TreeNode>>>,v:&mut Vec<i32>){
        let Some(node)=root else {return};
        v.push(node.borrow().val);
        Self::get_vec(node.borrow().left.clone(),v);
        Self::get_vec(node.borrow().right.clone(),v);

    }
}

  2. 提前判斷條件

    Leetcode 100. Same Tree

    題目：給兩顆樹判斷他是否相同

    輸入：p = [1,2,3], q = [1,2,3]

    輸出：true

    解法：用preorder判斷每個節點值是否相同，如果不同回傳false提前結束，如果相同繼續往下比較子樹直到葉節點。

    // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// 
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn is_same_tree(p: Option<Rc<RefCell<TreeNode>>>, q: Option<Rc<RefCell<TreeNode>>>) -> bool {

        match((p,q)) {
            (Some(node_p),Some(node_q))=>{
                if(node_p.borrow().val==node_q.borrow().val) {
                   let left = Self::is_same_tree(node_p.borrow().left.clone(),node_q.borrow().left.clone());
                    let right = Self::is_same_tree(node_p.borrow().right.clone(),node_q.borrow().right.clone());
                    return left & right
                } else {
                    return false
                }
            },
            (Some(node_p),None)=>{
                return false
            },
            (None,Some(node_q))=>{
                return false
            },
            (None,None)=>{
                return true
            }
        }

    }
}

    Leetcode 101. Symmetric Tree

    題目：判斷這棵樹是不是鏡像對稱

    輸入：root = [1,2,2,3,4,4,3]

    輸出：true

    解法：鏡像對稱，左子樹的左子樹=右子樹的右子樹，左子樹的右子樹=右子樹的左子樹，知道這個相等式就可以用leetcode 100 Same tree來解

    // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// 
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
        let Some(node)=root else { return true};
        let left = node.borrow().left.clone();
        let right = node.borrow().right.clone();
        Self::is_same(left,right)
    }


    pub fn is_same(p: Option<Rc<RefCell<TreeNode>>>,q: Option<Rc<RefCell<TreeNode>>>) -> bool {
        match(p,q) {
            (Some(p),Some(q))=>{
                if(p.borrow().val==q.borrow().val){
                    let outter_sub_tree=Self::is_same(p.borrow().left.clone(),q.borrow().right.clone());
                    let inner_sub_tree=Self::is_same(p.borrow().right.clone(),q.borrow().left.clone());
                    return outter_sub_tree & inner_sub_tree
                } else {
                    return false
                }
            },
            (Some(n),None)|(None,Some(n))=>{
                return false
            },
            (None,None)=>{
                return true
            }
        }
    }
}

中序遍歷 Inorder Traversal

先訪問左子樹，再訪問 root，最後訪問右子樹，走的順序D→B→E→A→C。

主要用途：

  1. 驗證一棵樹是不是 BST，並輸出有序資料

    Leetcode 98. Validate Binary Search Tree

    題目：給你一顆樹判斷是不是Binary Search Tree

    輸入：root = [2,1,3]

    輸出：true

    解法：BST特徵 左節點比父節點小，右子樹比父節點大，依照這特性我們可以用inorder來判斷節點的值是否遞增，遞增極為BST

    // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// 
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
     let mut prev:i64=i32::MIN as i64 -1;   
     Self::inorder(root,&mut prev)
    }

    pub fn inorder(root: Option<Rc<RefCell<TreeNode>>>,prev:&mut i64)->bool {
        let Some(node) = root else { return true};
        let b_n=node.borrow();
        // push left
        let l=Self::inorder(b_n.left.clone(),prev);

        // push parent
        let v = b_n.val as i64;
        if(*prev>=v){
            return false
        } else {
            *prev=v;
        }

        // push right
        let r=Self::inorder(b_n.right.clone(),prev);
        return l&r
    }
}

  2. 找最小 / 最大 / 第 K 小元素

    1. 最小值：Inorder 的第一個節點

    2. 最大值：Inorder 的最後一個節點

    3. 第 K 小：Inorder 走到第 k 次訪問時

    Leetcode 230. Kth Smallest Element in a BST

    題目：找第k小的節點

    輸入：root = [3,1,4,null,2], k = 1

    輸出：1

    // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// 
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn kth_smallest(root: Option<Rc<RefCell<TreeNode>>>, k: i32) -> i32 {
        let mut idx=0;
        let mut ans=0;
        Self::inorder(root,&mut idx,k,&mut ans);
        ans
    }

    pub fn inorder(root: Option<Rc<RefCell<TreeNode>>>,idx:&mut i32,k:i32,ans:&mut i32){
        let Some(node)=root else { return };
        let borrow_node= node.borrow();
        //left
        Self::inorder(borrow_node.left.clone(),idx,k,ans);
        //parent
        *idx+=1;
        if(*idx==k){
            *ans=borrow_node.val;
            return
        }
        //right
        Self::inorder(borrow_node.right.clone(),idx,k,ans);
    }
}

我們在看樹的題目時都會看到這樣的輸入[3,9,20,null,null,15,7]，所以能知道整個樹結構，那如果我們只有節點出現順序呢，能否知道整顆樹的結構？

重建樹

如果我們有preorder或是postorder順序配合inorder順序就能重建樹

Leetcode 105. Construct Binary Tree from Preorder and Inorder Traversal

題目：給一顆樹節點的preorder和inorder順序，重建回樹狀結構

輸入：preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

輸出：[3,9,20,null,null,15,7]

解法：

  1. 先找到root，preorder第一個值

  2. 知道root值後能在inorder切成[左子樹,跟節點,右子樹 ex 左子樹=[9] 右子樹=[15,20,7]

  3. 知道左子樹和右子樹數量後能在preorder切成[跟節點,左子樹,右子樹]

  4. 接著再對左子樹和右子數做步驟1~3直到全部排完

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
// 
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn build_tree(preorder: Vec<i32>, inorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        if(preorder.len()==0){
            return None
        }
        Self::build(&preorder[0..preorder.len()],&inorder[0..inorder.len()])
    }

    pub fn build(preorder:&[i32],inorder: &[i32])-> Option<Rc<RefCell<TreeNode>>> {
        if(preorder.len()==0){
            return None
        }
        let root_val = preorder[0];
        let mut idx = 0;
        for i in 0..inorder.len(){
           
            if(inorder[idx]==root_val){
                break
            }
            idx+=1;
        }

        let node = Rc::new(RefCell::new(
            TreeNode{
                val:root_val,
                left: Self::build(&preorder[1..idx+1],&inorder[0..idx]),
                right: Self::build(&preorder[idx+1..],&inorder[idx+1..]),
            }
        ));
        return Some(node)
    } 
}

Day24總結

  1. 前序遍歷 Preorder Traversal 做法
  2. 中序遍歷 Inorder Traversal 做法
  3. 利用前序遍歷和中序遍歷重建Binary tree

上一篇
用刷題來練RUST Day23 Tree & Depth First Search & Postorder Traversal
下一篇
用刷題來練RUST Day25 Binary Search Tree
系列文
用刷題來練RUST 共 28 篇
  1. 24
    用刷題來練RUST Day24 Inorder Traversal & Preorder Traversal
  2. 25
    用刷題來練RUST Day25 Binary Search Tree
  3. 26
    用刷題來練RUST Day26 Binary Tree BFS
  4. 27
    用刷題來練RUST Day27 Graph DFS & BFS
  5. 28
    用刷題來練RUST Day28 Implicit Graph & Adjacency List & Adjacency Matrix
完整目錄
圖片
  熱門推薦
圖片
{{ item.channelVendor }} | {{ item.webinarstarted }} |
{{ formatDate(item.duration) }}
直播中

尚未有邦友留言

立即登入留言
iThome鐵人賽
iThome鐵人賽
參賽組數
902 組
團體組數
37 組
累計文章數
17590 篇
完賽人數
218 人
iT+看影片追技術 看影片追技術 看更多
熱門tag 看更多
15th鐵人賽 16th鐵人賽 13th鐵人賽 14th鐵人賽 12th鐵人賽 17th鐵人賽 11th鐵人賽 鐵人賽 2019鐵人賽 javascript 2018鐵人賽 python 2017鐵人賽 windows php c# linux windows server css react
熱門問題
熱門回答
熱門文章
IT邦幫忙