樹 Tree

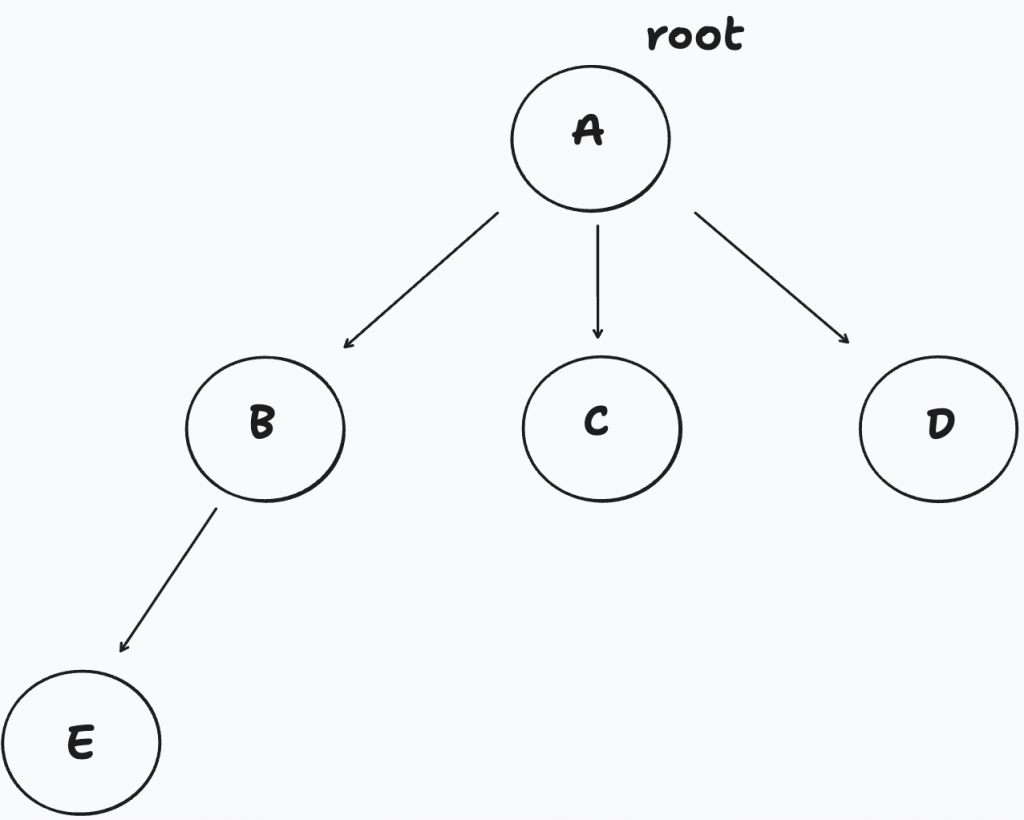
如圖來快速介紹下數的結構

1. A節點為這棵樹的根節點(root)

2. A是B、Ｃ、Ｄ的父節點(parent)

3. C、D、E沒有子節點 (children) 可以叫做葉節點**(leaf)**

4. 有N個節點的樹有N-1個邊

5. 不存在迴圈，所以到每個節點的方法只有一種

二元樹 Binary Tree

最多只有兩個子節點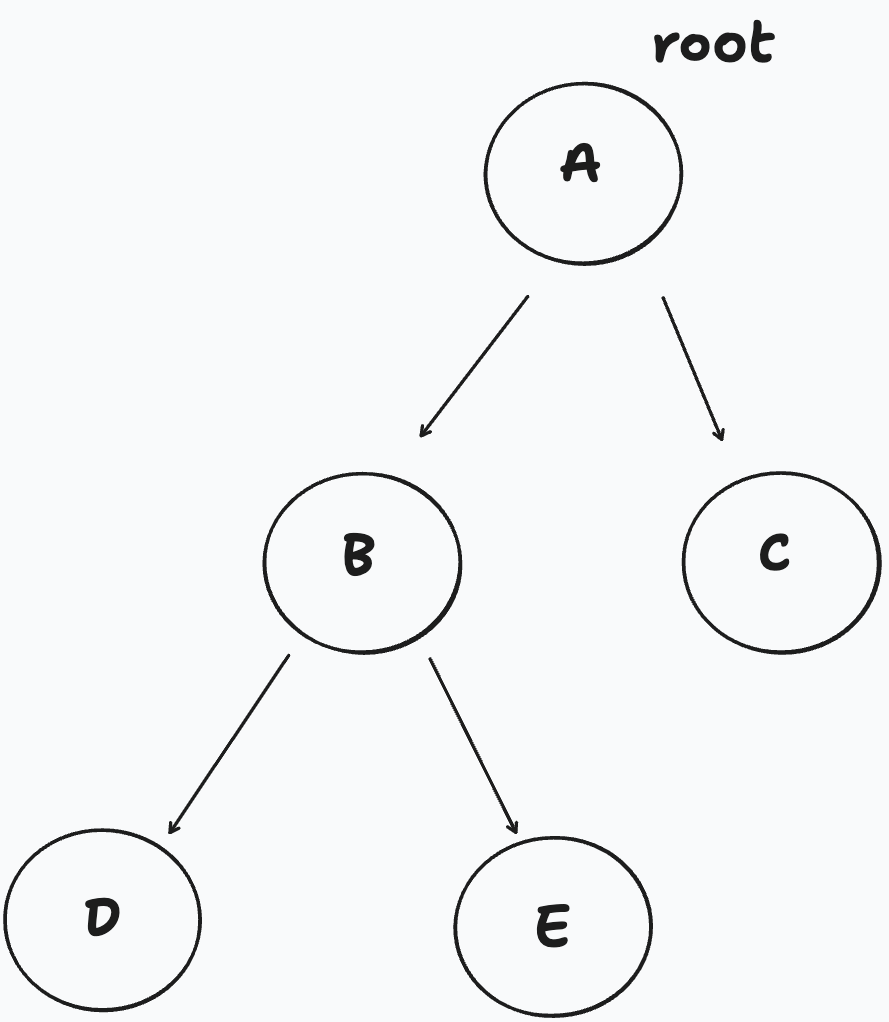

為何需要Tree

1. 查詢與插入

   1. Array → 查詢快 O(1)，插入刪除慢 O(n)

   2. LinkedList → 插入刪除快 O(1)，查詢慢 O(n)

   3. Tree (特別是平衡 BST) → 查詢、插入、刪除都 O(log n)

2. 有序操作

   1. HashMap 雖然查詢快 O(1)，但沒有排序也不能範圍查詢需要找完全部HashMap O(n)

   2. Tree（特別是 BST) inorder可得到排序結果，也能範圍查詢

3. 可以表示層級關係

之前提到的Max Heap就是樹的延伸，再拿大最大值時O(1)

深度優先搜尋 Depth First Search

以上圖為例，我們先往下找子節點，沒有子節點或是找完了在往同輩去找。

1. A→B

2. B→D

3. 沒有子節點回到B節點

4. B→E

5. 沒有子節點回到B節點

6. 子節點找完了回到A節點

7. A→C

8. 沒有子節點回到A節點

我們解一題練習先

Leetcode 104. Maximum Depth of Binary Tree

題目：給一顆樹返回的最大深度

輸入：[3,9,20,null,null,15,7]

輸出：3

     3
   /   \
  9     20
      /    \
     15     7

解法1：

1. 使用遞迴一直往下找到底，碰到Ｎone時回傳0

2. 從底往上回傳時，判斷左、右子樹深度回傳最深的+1大表以這棵節點為跟節點的最大深度

3. 跑完整顆樹回傳最大深度

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        match root {
            None => 0,
            Some(node) => {
                let l_depth = Self::max_depth(node.borrow().left.clone());
                let r_depth = Self::max_depth(node.borrow().right.clone());
                return l_depth.max(r_depth)+1;
            }
        }
    }
}

時間複雜度 O(n)，走完全部節點

解法2：

如stack中我們有看到遞迴能用stack來做

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        if let None = root {
            return 0
        }
        let mut stack:Vec<(Rc<RefCell<TreeNode>>,i32)> = Vec::new();
        let mut depth = 0;
        stack.push((root.unwrap(),1));

        while let Some((node,current_depth)) = stack.pop() {

            if let Some(right) = node.borrow().right.clone() {
                stack.push((right,current_depth+1));
            }
            if let Some(left) = node.borrow().left.clone() {
                stack.push((left,current_depth+1));
            }
            depth = depth.max(current_depth);
        }
        depth
    }
}

時間複雜度 O(n)，走完全部節點

後序遍歷 Postorder Traversal

像這種先訪問左子樹，再訪問右子樹，最後訪問 root，以上面二元樹的圖為例走的順序D→E→B→C→A，叫做Postorder Traversal

主要用途：

1. 計算樹的高度、節點數如 leetcode 104

2. 更新全域最佳解

   Leetcode 543. Diameter of Binary Tree

   題目：找到兩個最遠的節點路徑長

   解法：從底開始找左右子樹節點最長距離，並實時更新全域最長

   // Definition for a binary tree node.
   // #[derive(Debug, PartialEq, Eq)]
   // pub struct TreeNode {
   //   pub val: i32,
   //   pub left: Option<Rc<RefCell<TreeNode>>>,
   //   pub right: Option<Rc<RefCell<TreeNode>>>,
   // }
   // 
   // impl TreeNode {
   //   #[inline]
   //   pub fn new(val: i32) -> Self {
   //     TreeNode {
   //       val,
   //       left: None,
   //       right: None
   //     }
   //   }
   // }
   
   // current left path len + right path len if greater then prev max update
   // after recursion return max length
   use std::rc::Rc;
   use std::cell::RefCell;
   impl Solution {
       pub fn diameter_of_binary_tree(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
           let mut max_len=0;
   
           Self::postorder(root,&mut max_len);
           max_len    
       }
   
       pub fn postorder(root: Option<Rc<RefCell<TreeNode>>>,max_len:&mut i32)->i32{
           let Some(node)=root else { return -1};
           let b_n = node.borrow();
           let left_path=Self::postorder(b_n.left.clone(),max_len);
           let right_path=Self::postorder(b_n.right.clone(),max_len);
           if(*max_len<left_path+right_path+2){
               *max_len=left_path+right_path+2
           }
           return left_path.max(right_path)+1
       }
   }
   

3. 刪除整棵樹時，先刪子樹再刪 root

   Leetcode 1325. Delete Leaves With a Given Value

   題目：給一個目標值，刪掉等於這個值的葉節點

   輸入：root = [1,2,3,2,null,2,4], target = 2

   輸出：[1,null,3,null,4]

   解法：從最底部開始刪，避免上層節點判斷到要刪但未刪得子節點而沒刪到。

   // Definition for a binary tree node.
   // #[derive(Debug, PartialEq, Eq)]
   // pub struct TreeNode {
   //   pub val: i32,
   //   pub left: Option<Rc<RefCell<TreeNode>>>,
   //   pub right: Option<Rc<RefCell<TreeNode>>>,
   // }
   // 
   // impl TreeNode {
   //   #[inline]
   //   pub fn new(val: i32) -> Self {
   //     TreeNode {
   //       val,
   //       left: None,
   //       right: None
   //     }
   //   }
   // }
   use std::rc::Rc;
   use std::cell::RefCell;
   impl Solution {
       pub fn remove_leaf_nodes(root: Option<Rc<RefCell<TreeNode>>>, target: i32) -> Option<Rc<RefCell<TreeNode>>> {
           Self::post_order_delete(root,target)
       }
   
       pub fn post_order_delete(root: Option<Rc<RefCell<TreeNode>>>, target: i32) -> Option<Rc<RefCell<TreeNode>>> {
           let Some(node)=root else {return None};
           let n_b = node.borrow();
   
           let left = Self::post_order_delete(n_b.left.clone(),target);
           let right = Self::post_order_delete(n_b.right.clone(),target);
           if(n_b.val==target&&left.is_none()&&right.is_none()){
               return None
           }
           return Some(Rc::new(RefCell::new(TreeNode{
               val:n_b.val,
               left:left,
               right:right
           })))
       }
   }
   

Day23總結

1. 介紹樹的結構
2. 介紹深度優先搜尋 Depth First Search
3. 後序遍歷 Postorder Traversal 實作

參考資料

1. https://www.geeksforgeeks.org/dsa/dfs-traversal-of-a-tree-using-recursion/