鐵人賽過了今天就算完成helf了!我們也完成了三個主題的複習:

• NET工程師的R環境
• R語言基礎
• R語言資料介面

自己跑過半馬10幾次，就是沒跑過全程馬拉松，繼續往前跑，下半helf主題。

• R語言的資料視覺化
• 簡單的機器學習演算法

Day12-Day14複習了外部資料介面，有了資料集，接下來我們就可以開始觀察資料、分析資料了。

統計是資料分析的基礎，今天先選擇幾個簡單的敘述統計分析函數來複習:

敘述統計是描述資料分佈的特性，可以描述資料的:

• 集中趨勢(平均數(mean)、中位數(median)、眾數(mode))
• 離散趨勢(標準差(sd)、變異數(var)、變異係數(cv)、全距(range)、四分位(Quartile))

我們在資料夾MyR新增一支Day15.R

集中趨勢

先觀察一個維度資料，在Day15.R中輸入程式碼

n <- c(1,1,2,4,6) 
plot(n, pch = 17, col = "blue", cex =2) 

執行結果:

X軸是數值Index，Y軸是數值

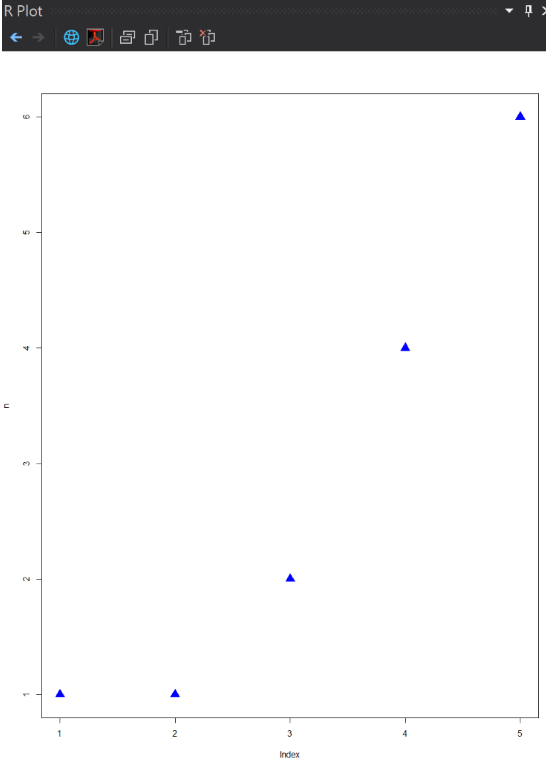
接著作一維資料簡單的統計，在Day15.R中輸入程式碼

#總合 
sum(n) 
 
#平均數 總合除個數 
mean(n) 
 
#中位數:將資料由小到大，位置居中者，就是中位數  
median(n) 
 
#眾數:一組資料中，出現最多次數的值 
as.numeric(names(table(n)))[which.max(table(n))] 
 
#畫平均數的點 
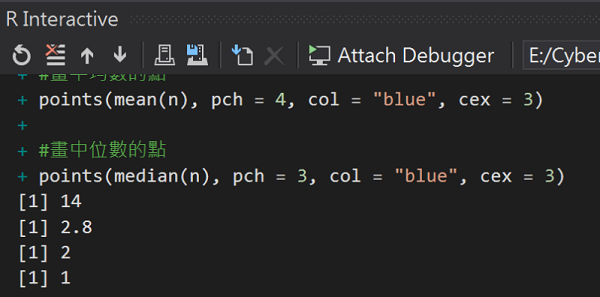
points(mean(n), pch = 4, col = "blue", cex = 3) 
 
#畫中位數的點 
points(median(n), pch = 3, col = "blue", cex = 3) 

R互動視窗執行結果:

• 總和14
• 平均數2.8
• 中位數是2
• 眾數是1

R plot視窗執行結果

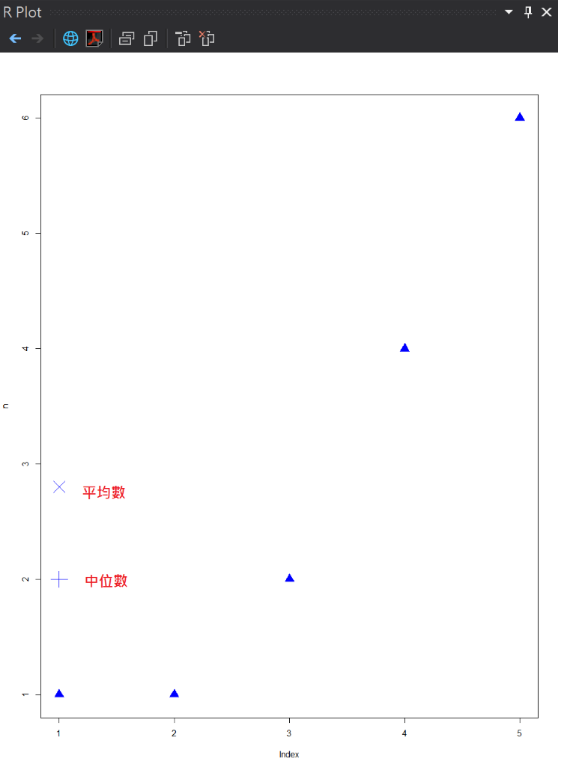
集中趨勢在2-3的值間。

離散趨勢

有時候大起大落的表現會讓平均數(Mean)失真，要觀察選手表現是否穩定，標準差(sd:standard deviation)等離散趨勢函數就可以反應比較真實的數值離散程度。

在Day15.R中輸入程式碼

n <- (1:10) 
 
#標準差  
sd(n) 
 
#變異數 
var(n) 
sd(n) ^ 2 
 
#變異係數 
cv <- 100 * sd(n) / mean(n) 
cv 
 
#全距(最大值減最小值) 
range(n)[2] - range(n)[1] 
 
#四分位:把資料切分為四等分，中間的三條線就是四分位，Q1=P25,Q2=P50,Q3=75 
Q1 <- quantile(n, 1 / 4) 
Q2 <- quantile(n, 2 / 4) 
Q3 <- quantile(n, 3 / 4) 
Q1 
Q2 
Q3 
 
#IQR = Q3-Q1 
b <- Q3 - Q1 == IQR(n) 
b 

執行結果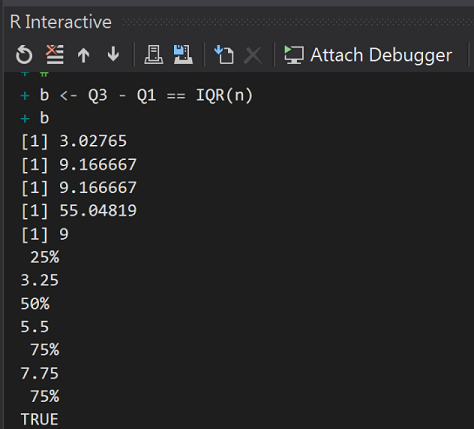

• 標準差:3.02
• 變異數:9.16
• 變異係數:55.04
• 全距:9
• Q1:3.25
• Q2:5.5
• Q3:7.75

Tips

一次總結數據
在Day15.R中輸入程式碼

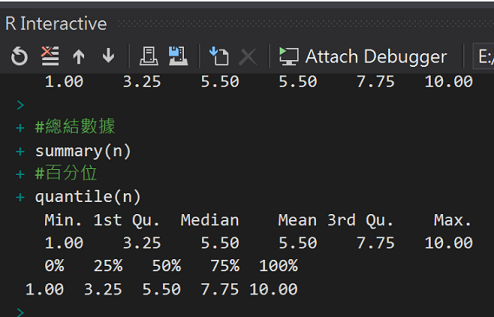
#總結數據(超好用) 
summary(n) 
#百分位 
quantile(n) 

執行結果

THE ROCK

2014.10月攝於直布羅陀半島,英屬地