正所謂物以類聚，人以群分，想要問的問題有標準答案時，我們可以讓機器用分類演算法學習，歸納出資料的平均機率或是資料間的結構關係，但沒有標準答案的問題時，也許我們就可以使用非監督式學習下(unsupervised learning)的分群演算法來分類資料間的結構。

因為沒有先畫好線，怎麼下這一刀，要下幾刀在料理界上通常最後變成是一種藝術上的問題，還好R語言也有的學，我們來找出平均相似的群集(Cluster)資料。

專案新增一支Day29.R

k-means (clustering)

中文是K平均演算法， 一直以來用k-means都是懵懵懂懂的，只知道用k來分出幾個k群，上機器學習課程時，筆記到了兩個很重要的學習目標:

• 組內差異小
• 組間差異大

由於訓練資料集是沒有答案的， 所以沒有對與錯，只要符合上面兩個特點。

為了實際體驗分群結果，我們繼續使用鳶尾花資料集(iris)，分別用標準答案先畫第一個圖，然後用k-means指定3個分群結果來畫。

1. 拿答案Species(亞種)欄位畫
2. 利用分群演算法的結果畫

# (1)直接用亞種結果畫分佈(花瓣的長寬) 
plot(formula = Petal.Length ~ Petal.Width, data = iris, col = iris$Species)


#(2)分群畫圖 
# 建立一個分群模型 
data <- iris[-5] #去除第5個資料行    
##分3群，nstart=10 defaut執行10次  收斂資料區 
km <- kmeans(data, centers = 3, nstart = 10)

#跑分群之後畫分佈 
plot(formula = Petal.Length ~ Petal.Width, data = data, col = km$cluster, main = "將鳶尾花做分群", xlab = "花瓣寬度", ylab = "花瓣長度")

標準答案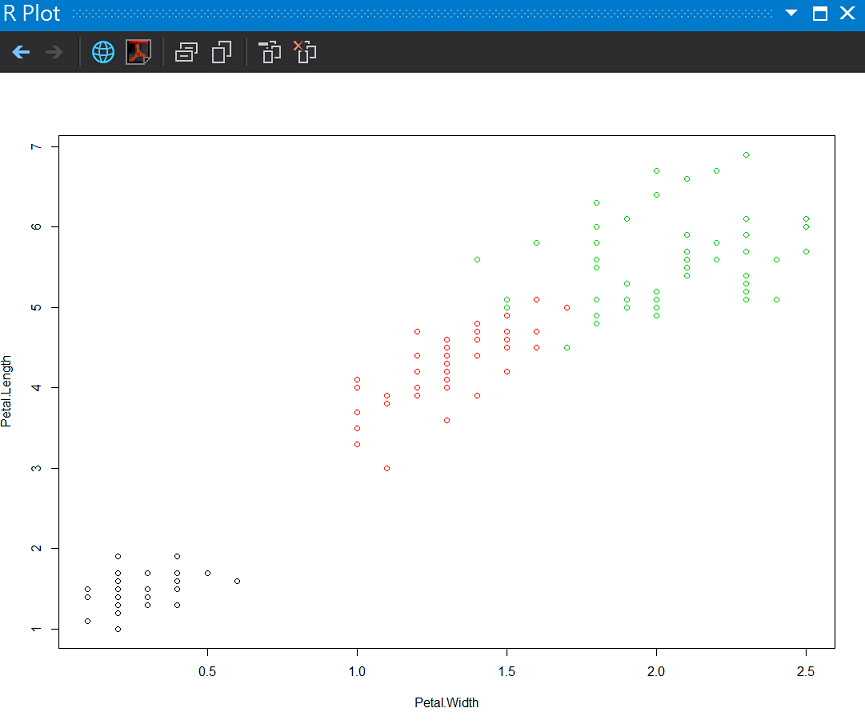

分群答案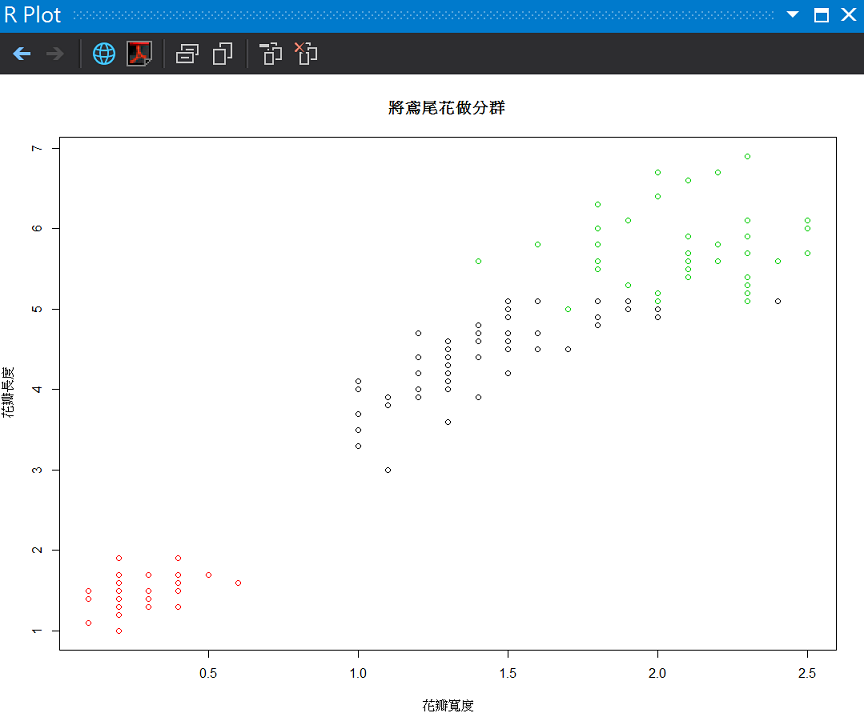

由於事前知道3-Means是實際分群組數，分群的效果很棒!

利用分群結果畫圖(散佈圖加上密度2D)

ggplot(data, aes(x = Petal.Length, y = Petal.Width)) +
geom_point(aes(color = factor(km$cluster))) +
stat_density2d(aes(color = factor(km$cluster)))

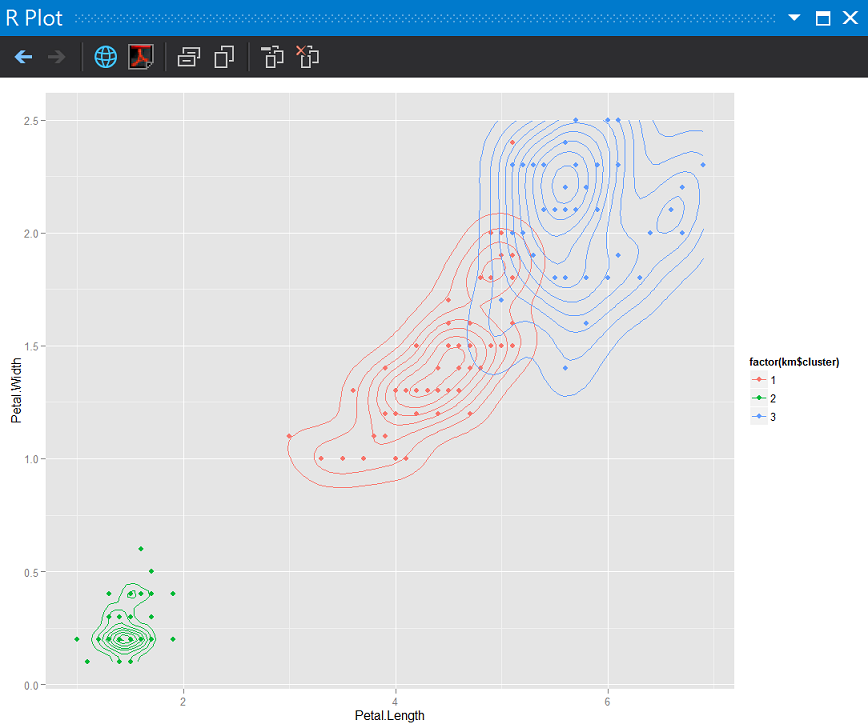
她沒辦法知道每一個群聚組是哪一種鳶尾花的亞種，會直接以1,2,3代號來分。

西班牙現代建築師高第曾說

直線屬於人類，曲線屬於上帝。

鳶尾花是自然科學，屬於上帝。

評估分群模型　　

還記得剛剛提到的組內差異小、組間差異大的學習目標，在衡量分群演算法的表現上，今年機器學習課程學到了用WSS/TSS比例預估。

• 組內距離平方和WSS(Within Cluster Sum of Squares) 越小越好
• 組間距離平方和BSS(Between Cluster Sum of Squares) 越大越好
• 總離均差平方和TSS(Total Cluster Sum of Squares)

(WSS <- km$tot.withinss)
(BSS <- km$betweenss)
(TSS <- BSS + WSS)
(ratio <- WSS / TSS)

K值的決定

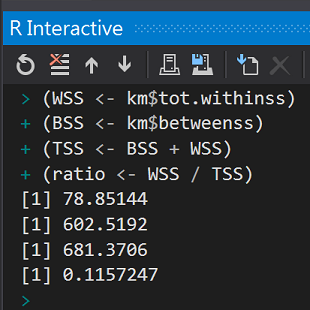
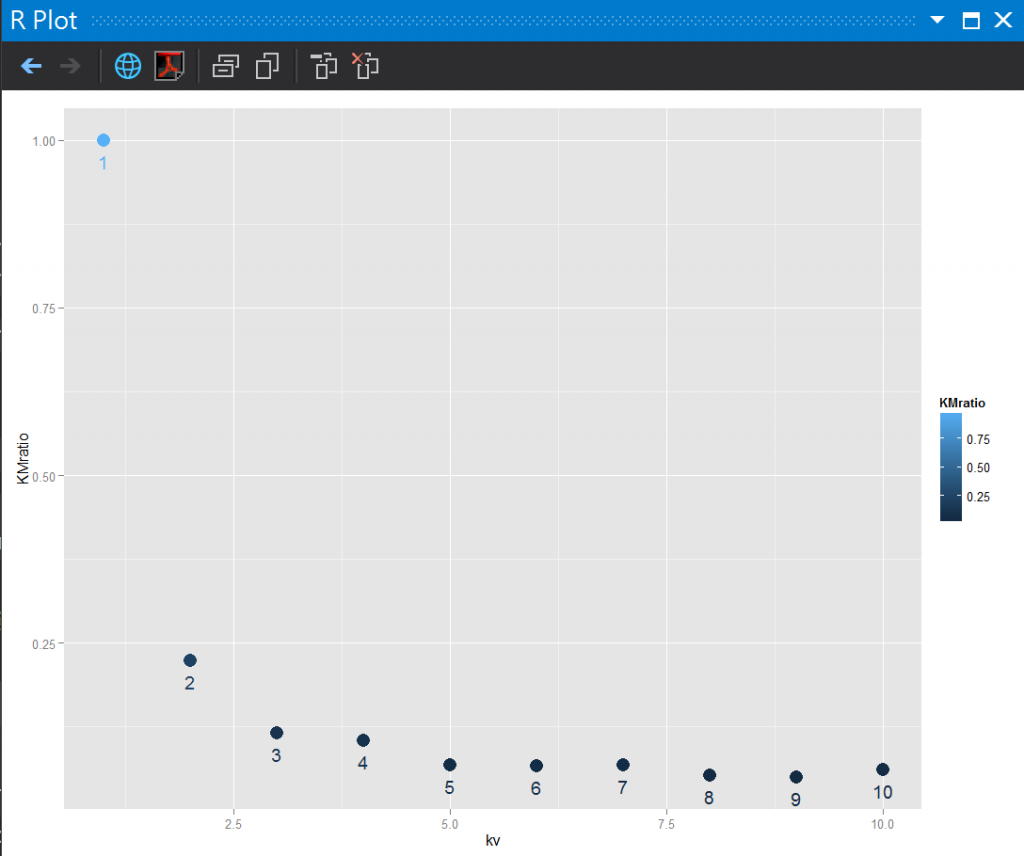
這邊我們可以仿照最近鄰居K-NN的方式比較出最佳WSS/TSS比例值的K Value。

library(ggplot2)
klist <- seq(1:10)
knnFunction <- function(x) {
    kms <- kmeans(data, centers = x, nstart = 1)
    ratio <- kms$tot.withinss / (kms$tot.withinss + kms$betweenss)
}
ratios <- sapply(klist, knnFunction)

# k value與準確度視覺化
df <- data.frame(
       kv = klist, KMratio = accuracies)

ggplot(df, aes(x = kv, y = KMratio, label = kv, color = KMratio)) +
geom_point(size = 5) + geom_text(vjust = 2)

• 取出k值最小但WSS/TSS越貼近0的k value。
• 那個1-mean好像有分等於沒分，WSS/TSS ratio值為1。
• 最後就是雖然都有k，但k平均演算法與k近鄰演算法沒有任何關係。

第29天了！

參考

Wiki k-平均演算法
#https://zh.wikipedia.org/wiki/K-%E5%B9%B3%E5%9D%87%E7%AE%97%E6%B3%95

陳鍾誠教授的網站
http://ccckmit.wikidot.com/ai:kmeans

熊布朗宮山丘

2013.05攝於vienna,Austria