第28天了!今天豪邁的把鐵人賽前備用的分類演算法題目一次乾了,喉嚨借我過一下。
先準備今天的環境,專案新增一支Day28.R
載入鳶尾花(iris)資料集,分成訓練組及測試組
#(1)載入iris資料
data(iris)
#(2)畫散佈圖
library(ggplot2)
#花萼長寬分佈
ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width)) + geom_point(aes(color = Species))
#花瓣長寬分佈
ggplot(iris, aes(x = Petal.Length, y = Petal.Width)) + geom_point(aes(color = Species))
#(3)切分訓練及測試樣本
#設定亂數種子
set.seed(1111)
#樣本筆數
n <- nrow(iris)
#取出樣本數的idx
t_idx <- sample(seq_len(n), size = round(0.7 * n))
#訓練資料與測試資料比例: 70%建模,30%驗證
traindata <- iris[t_idx,]
testdata <- iris[ - t_idx,]
花萼長寬分佈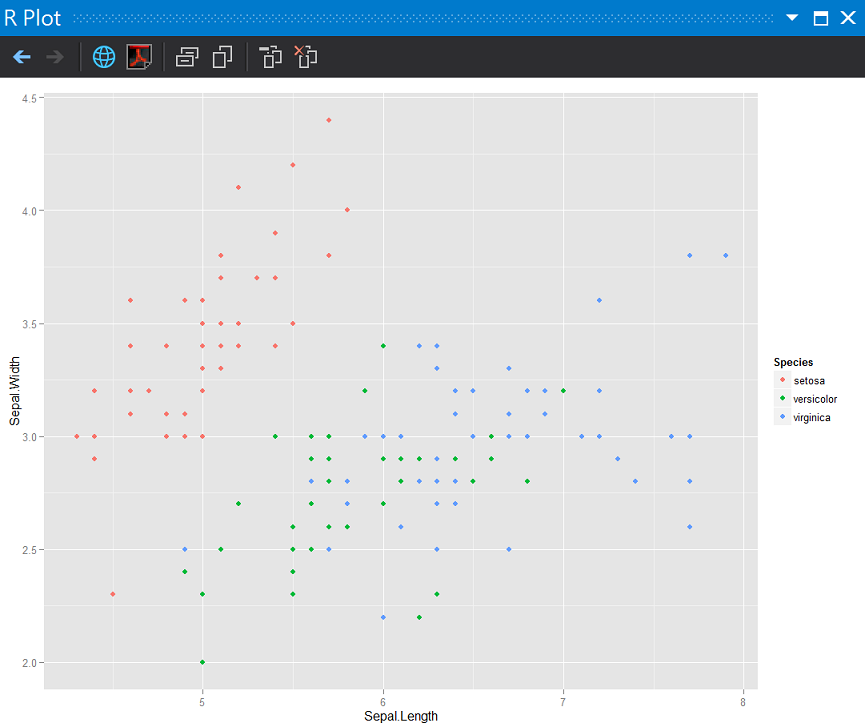
花瓣長寬分佈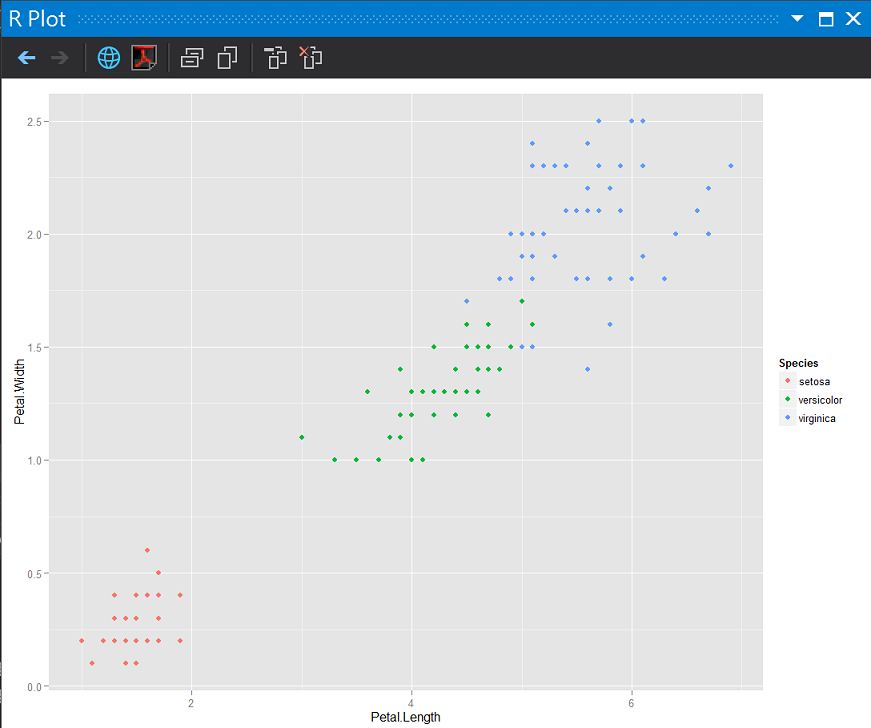
如果我們知道亞種(上圖中的顏色)的標準答案,不管用花萼或是花瓣好像都可以肉眼分辨出來,但如果我們不知道標準答案時:
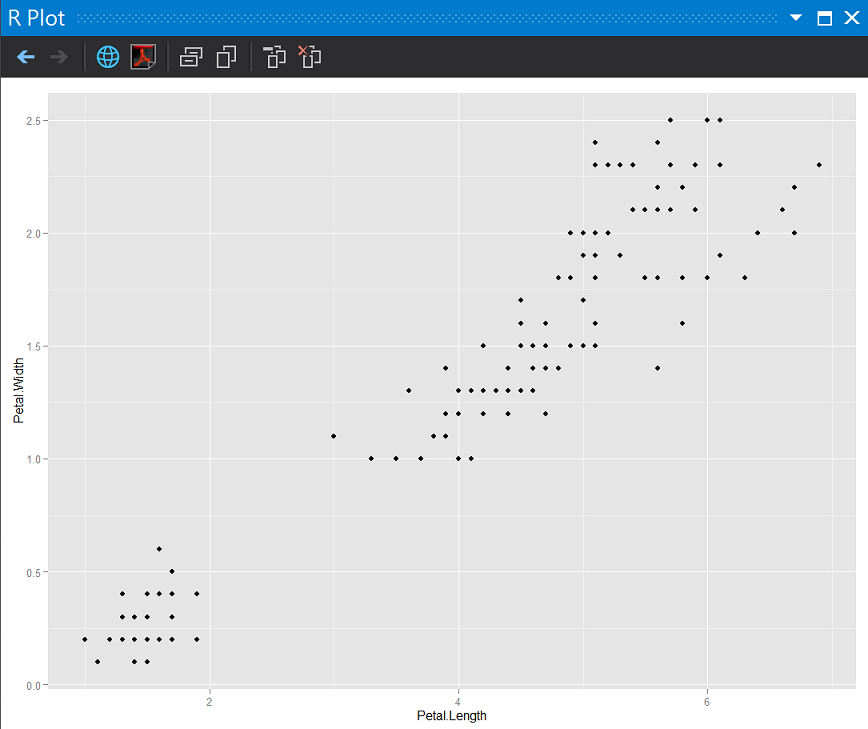
前面兩天複習到的決策樹與類神經(Artificial neural network)都可以幫助我們完成分類問題,我們今天來試試其他分類演算法。
K-NN使用點間的距離為分類標準,當新的觀測值準備預測時,演算法會計算出和她接近最多的類目標點,比方說,k值=5,觀測值比較靠近其中3個目標點時,演算法就會採用多數票來決定分類結果。
#安裝並載入class套件
library(class)
library(dplyr)
#(參數1)準備訓練樣本組答案
trainLabels <- traindata$Species
#(參數2)(參數3)去除兩個樣本組答案
knnTrain <- traindata[, - c(5)]
knnTest <- testdata[, - c(5)]
#計算k值(幾個鄰居)通常可以用資料數的平方根
kv <- round(sqrt(n))
kv
#(4)建立模型
prediction <- knn(train = knnTrain, test = knnTest, cl = trainLabels, k = kv)
#(5)評估正確性
cm <- table(x = testdata$Species, y = prediction, dnn = c("實際", "預測"))
cm
knnaccuracy <- sum(diag(cm)) / sum(cm)
knnaccuracy
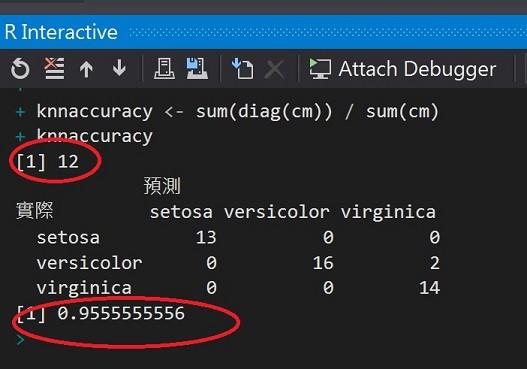
當k值=12時,準確度大約95.5%,已經是相當高的預測了。
分別使用knn結果對訓練組資料及測試資料畫散佈圖加上密度2D圖
#利用knn結果畫圖
#訓練組
knnTrain$Species <- trainLabels
ggplot(knnTrain, aes(x = Petal.Length, y = Petal.Width)) + geom_point(aes(color = Species)) +
stat_density2d(aes(color = Species))
#測試組
knnTest$Species <- prediction
ggplot(knnTest, aes(x = Petal.Length, y = Petal.Width), n = 10) + geom_point(aes(color = Species)) +
stat_density2d(aes(color = Species), h = 0.6)
訓練組
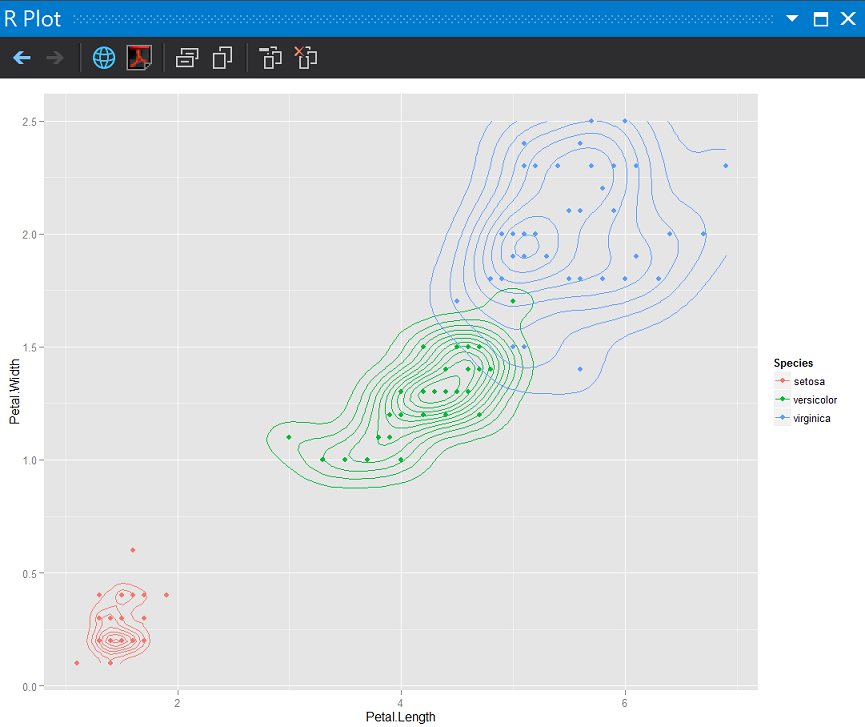
測試組
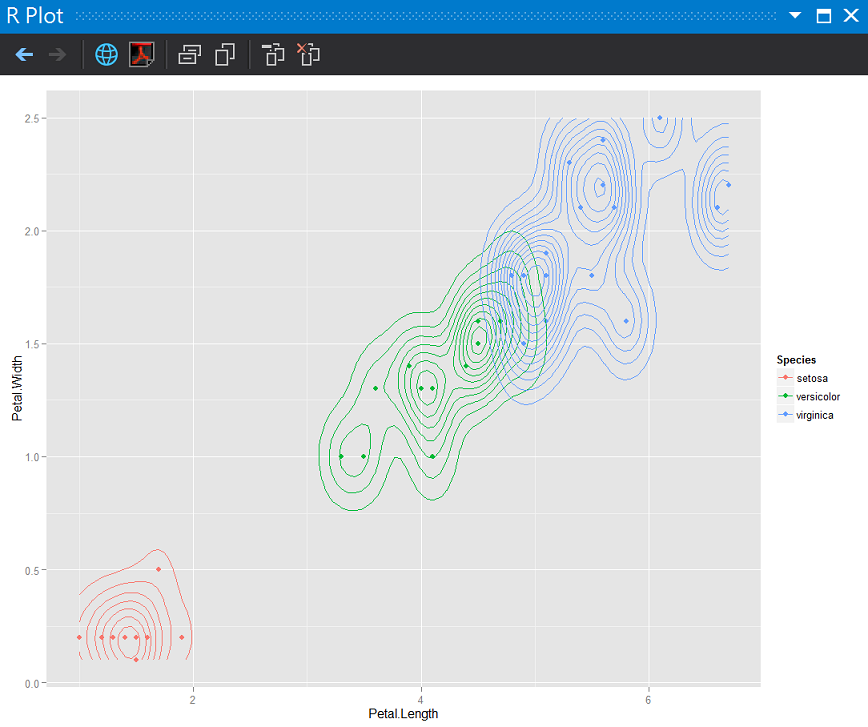
Knn這次預測的問題在virginica和versicolor兩個亞種同時位在DMZ時(分佈太接近),會有誤判。
除了用訓練組平方根計算K值,另外一種方式就是比較k值的準確度(accuracy),作法就是用剛剛平方根算出來的k值微調(tuning)到k+k的距離,然後重新跑模型測試各種k值準確度(accuracy),最後取取最佳值出來。
k值太小會有overfitting的問題,思考了一下1-nn的概念,如果每個訓練用的觀測值都自成一格,在分類上的效果好像就失去了,所以也許比較的範圍可以從2-2k。
# 選擇k value
klist <- seq(1:(kv + kv))
knnFunction <- function(x, knnTrain, knnTest, trainLabels, testLabels) {
prediction <- knn(train = knnTrain, test = knnTest, cl = trainLabels, k = x)
cm <- table(x = testLabels, y = prediction)
accuracy <- sum(diag(cm)) / sum(cm)
}
accuracies <- sapply(klist, knnFunction, knnTrain = knnTrain, knnTest = knnTest, trainLabels = trainLabels, testLabels = testdata$Species)
# k value與準確度視覺化
df <- data.frame(
kv = klist, accuracy = accuracies)
ggplot(df, aes(x = kv, y = accuracy, label = kv, color = accuracy)) +
geom_point(size = 5) + geom_text(vjust = 2)
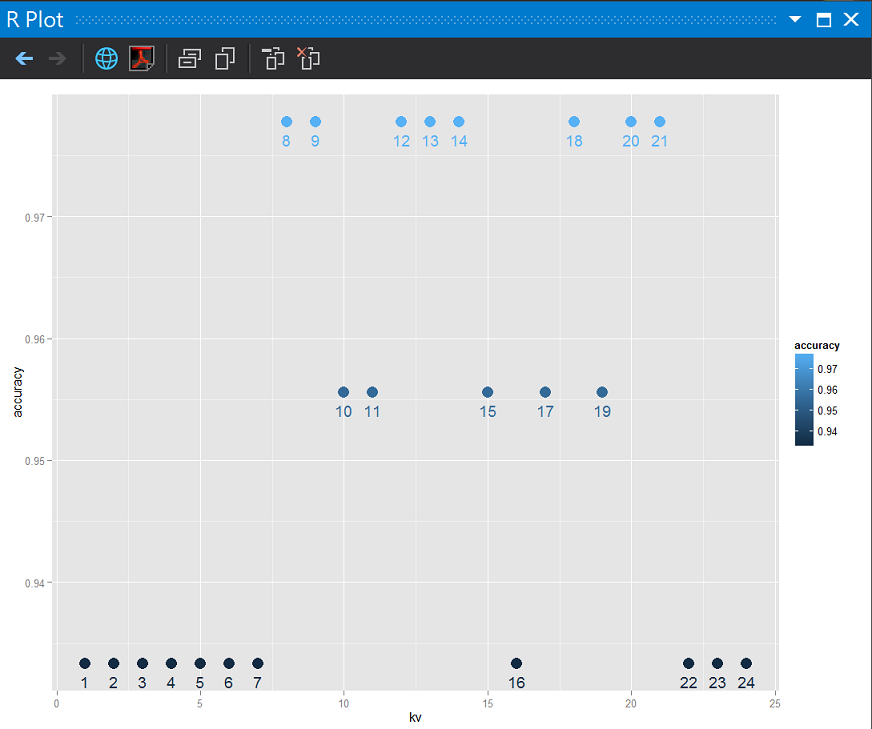
這樣的概念也可以用在幾種分類器間的選擇,像是同時跑決策樹、類神經及knn取最佳解或是幾種演算法的結果再機器學習一次。
使用SVM及樸素貝氏分類器之前,我們需要載入套件e1071:Misc Functions of the Department of Statistics。
SVM WIKI
分類資料是機器學習中的一項常見任務。 假設某些給定的資料點各自屬於兩個類之一,而目標是確定新資料點將在哪個類中。對於支援向量機來說,資料點被視為 p 維向量,而我們想知道是否可以用 (p-1)維超平面來分開這些點。這就是所謂的線性分類器。可能有許多超平面可以把資料分類。最佳超平面的一個合理選擇是以最大間隔把兩個類分開的超平面。因此,我們要選擇能夠讓到每邊最近的資料點的距離最大化的超平面。如果存在這樣的超平面,則稱為最大間隔超平面,而其定義的線性分類器被稱為最大間隔分類器,或者叫做最佳穩定性感知器。
#載入套件
library(e1071)
# 建立模型
svmM <- svm(Species ~ ., data = traindata, probability = TRUE)
# 預測
results <- predict(svmM, testdata, probability = TRUE)
# 評估
cm <- table(x = testdata$Species, y = results)
cm
SVMaccuracy <- sum(diag(cm)) / sum(cm)
SVMaccuracy
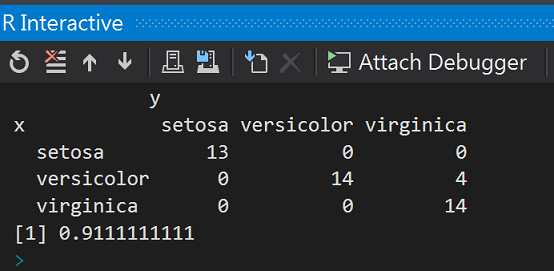
準確度(accuracy):91%
樸素貝氏分類器(Naive Bayes Classifier),也看過有人翻譯樸素貝葉斯算法。
如果觀測資料具有條件獨立,樸素貝氏分類收斂速度非常過速,貝氏分類器可以直接使用條件機率相乘計算出分佈。
不過樸素貝氏分類也有缺點,她沒辦法學習到x變數間共同出現的機率。
nbcm <- naiveBayes(Species ~ ., data = traindata)
results <- predict(nbcm, testdata)
# 評估
cm <- table(x = testdata$Species, y = results)
cm
naiveBayesaccuracy <- sum(diag(cm)) / sum(cm)
naiveBayesaccuracy
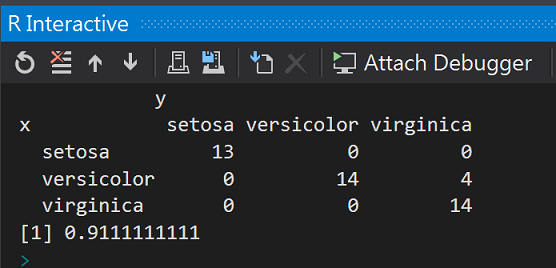
準確度(accuracy):91%,不知道是不是都來自e1071套件,所以和svm英雄所見相同。
今天的預測結果
df <- data.frame(perf = c(knnaccuracy, SVMaccuracy, naiveBayesaccuracy), name = c("KNN", "SVM", "naiveBay"));
ggplot(df, aes(x = name, y = perf, color = name, label = perf)) +
geom_point(size = 5) + geom_text(vjust = 2)
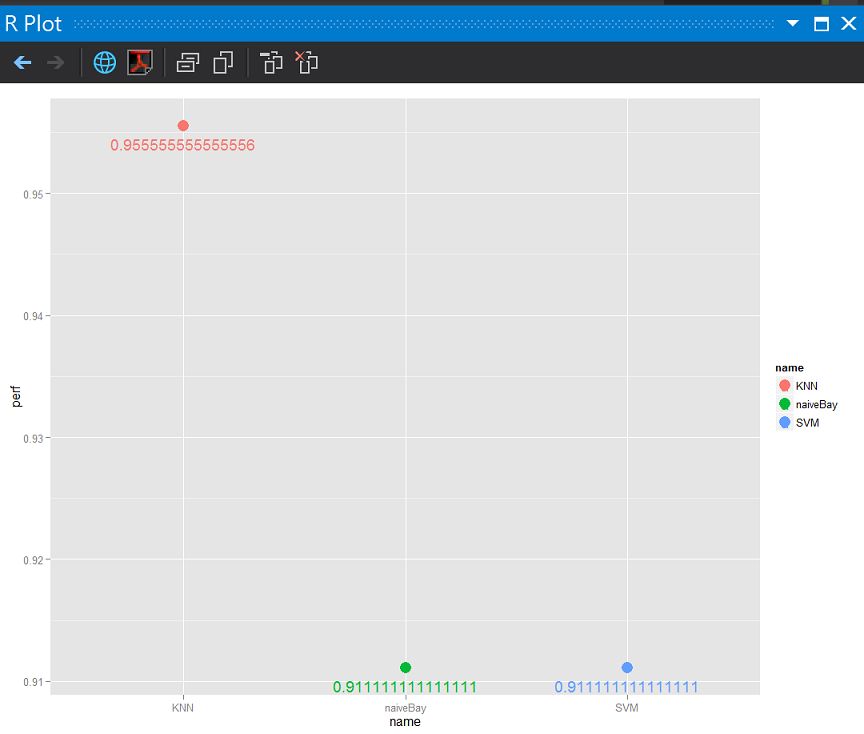
只有今天喔!
支持向量機 wiki
https://zh.wikipedia.org/wiki/%E6%94%AF%E6%8C%81%E5%90%91%E9%87%8F%E6%9C%BA
無限期支持向量機
https://www.facebook.com/unlimitedsvm/posts/753660647998775
http://www.csie.ntu.edu.tw/~cjlin/libsvm/
選擇鄰居:
庫倫諾夫
2013.05攝於Český Krumlov,Czech
帖契
2013.05攝於telc,Czech
