Day26 R語言機器學習之決策樹與隨機森林

2017 iT 邦幫忙鐵人賽

DAY 26

Big Data

R語言與機器學習見面會系列第 26 篇

2017鐵人賽 r語言機器學習

StanleyJui

2016-12-26 06:44:00

49453 瀏覽

分享至

前面幾天我們用幾種常見的迴歸解決了計算數值的數學題目以及回答是或否的是非題目，接下來，我們來讓機器學習用分類(Classification)的方式幫我們回答選擇題。

分類演算法:

分類法(Classification)也是監督式學習(Supervised Learning)的一種，根據已知分類的資料集將未分類的資料集完成分類，常見的分類演算法有:

決策樹、隨機森林
類神經網路
最近鄰居法
樸素貝氏分類及貝氏信念網路

今天來複習決策樹。

決策樹(Decision Tree)

決策樹(Decision Tree)是以樹狀為基礎的演算法，透過歸納規則將資料從樹根開始分類，一節一節尋找最佳分割點來將資料分成為小單位的集合，中間有時也會透過園丁修剪，而成為一顆樹形美麗的決策樹。

不過當訓練資料集內的數目太少，而變數太多時，分類的效果會變差，另外，決策樹在分類上屬於固定的路徑，沒辦法像類神經在分類過程有容錯能力，有時也會有同時使用決策樹結合類神經網路(Artificial neural network)或是採用隨機森林(Random Forest)作預測。

專案新增一支Day26.R

使用決策樹演算法

這邊我們使用與Day24 R語言機器學習之羅吉斯迴歸相同的AER Package中的信用卡資料集練習，除了羅吉斯迴歸分析，我們也試著使用決策樹分析來一起決定結果。

#安裝package 
install.packages("rpart")
install.packages("rpart.plot")
install.packages("rattle")

#載入library 
library("rpart")
library("rpart.plot")
library("rattle")


#載入AER Package(AER: Applied Econometrics with R)
#install.packages("AER")
library(AER)

#(1)載入creditcard資料集(包含1,319筆觀察測試，共有12個變數)
data(CreditCard)

#假設我們只要以下欄位(card:是否核准卡片、信用貶弱報告數、年齡、收入(美金)、自有住宅狀況、往來年月)
bankcard <- subset(CreditCard, select = c(card, reports, age, income, owner, months))

#將是否核准卡片轉換為0/1數值
bankcard$card <- ifelse(bankcard$card == "yes", 1, 0);

將將資料分為訓練與測試組

#(2)測試模型
#取得總筆數
n <- nrow(bankcard)
#設定隨機數種子
set.seed(1117)
#將數據順序重新排列
newbankcard <- bankcard[sample(n),]

#取出樣本數的idx
t_idx <- sample(seq_len(n), size = round(0.7 * n))

#訓練資料與測試資料比例: 70%建模，30%驗證
traindata <- newbankcard[t_idx,]
testdata <- newbankcard[ - t_idx,]

我們使用rpart()來建立決策樹模型，這邊的method參數可以選擇分類樹class或迴歸樹anova兩種方式。
接著使用rattle套件來圖解厲害的決策樹。

#(3)建立決策樹模型 
dtreeM <- rpart(formula = card ~ ., data = traindata, method = "class", control = rpart.control(cp = 0.001))

#(4)用rattle畫出厲害的決策樹(Rx: rxDTree)
fancyRpartPlot(dtreeM)

決策樹預測及準確率

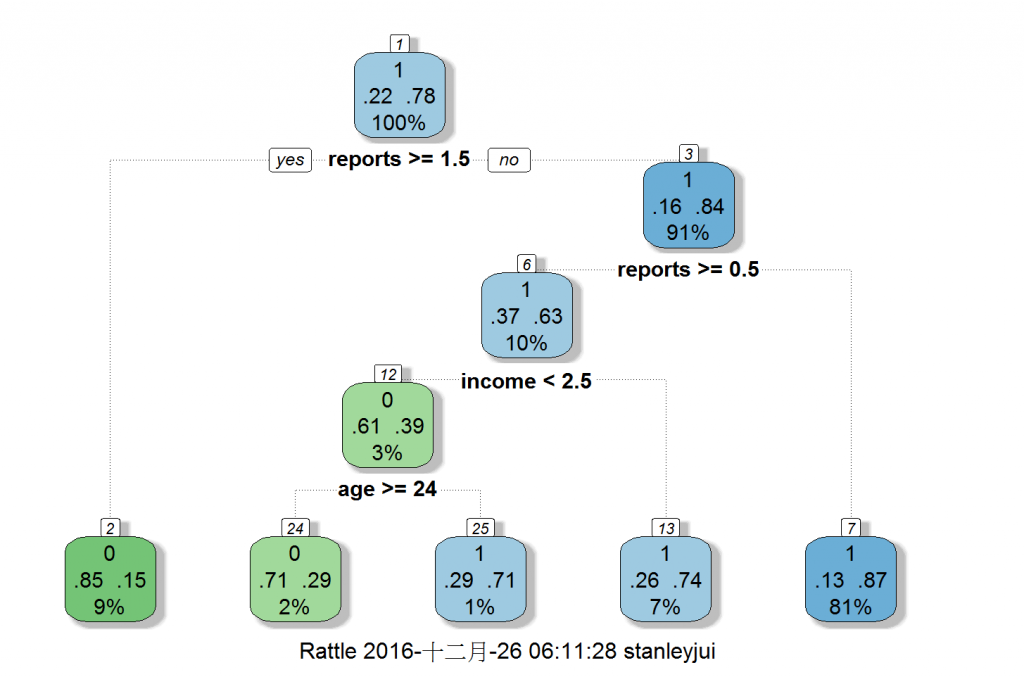
我們可以使用混淆矩陣(confusion matrix)及準確率(Accuracy)觀察模型表現

#(5)預測
result <- predict(dtreeM, newdata = testdata, type = "class")
#(6)建立混淆矩陣(confusion matrix)觀察模型表現
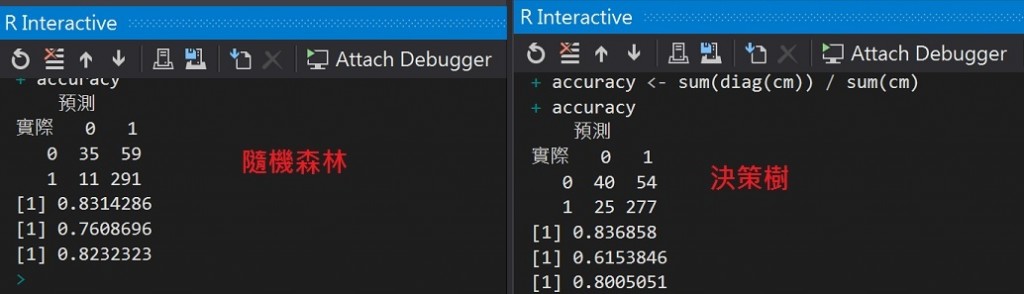
cm <- table(testdata$card, result, dnn = c("實際", "預測"))
cm

#(6)正確率
#計算核準卡正確率
cm[4] / sum(cm[, 2])

#計算拒補件正確率
cm[1] / sum(cm[, 1])

#整體準確率(取出對角/總數)
accuracy <- sum(diag(cm)) / sum(cm)
accuracy

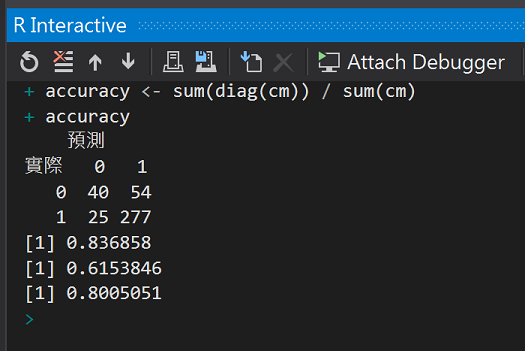
整體準確率大約80%，和前面[Day24 R語言機器學習之羅吉斯迴歸](Day24 R語言機器學習之羅吉斯迴歸)的82%差不多。

條件推論樹(Conditional Inference Tree)

在決策樹中還有一種條件推論樹可以使用，函式是ctree()，我們使用鳶尾花資料集(iris)的複習。

#install.packages("party") 
library(party)

ct <- ctree(Species ~ ., data = iris)
plot(ct, main = "條件推論樹")
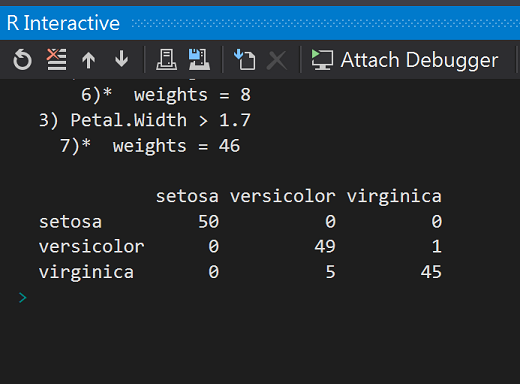
table(iris$Species, predict(ct))

圖解條件推論樹

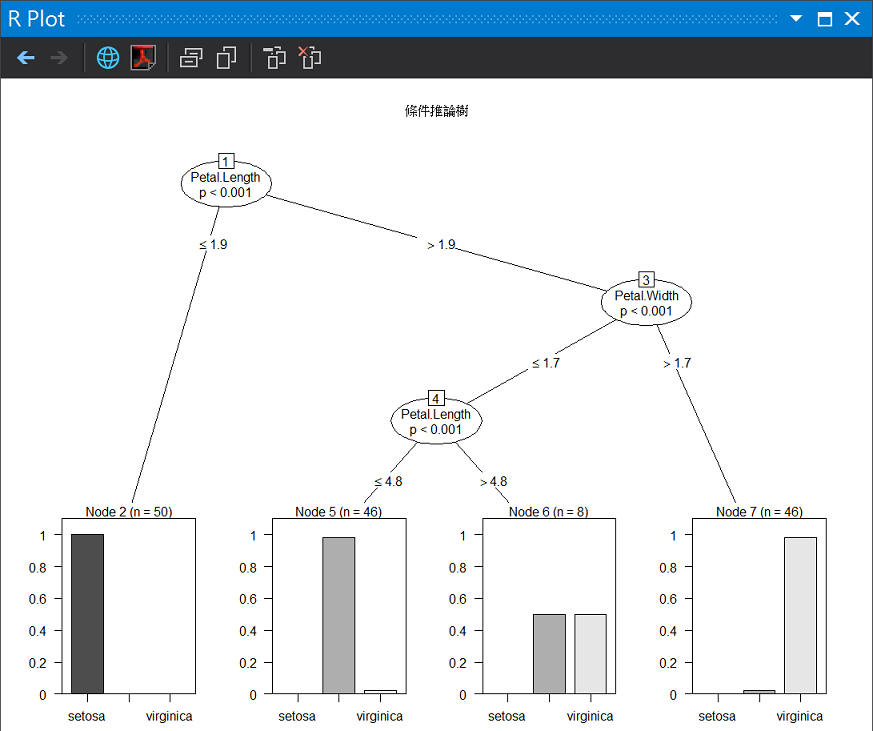
從混淆矩陣可以發現，150筆觀測資料中，只有6筆資料沒辦法正確分類。

隨機森林(Random Forests)

正所謂一箭易折,十箭難斷，為了能讓準確度更高，有時我們會結合多個決策樹的分類器來作預測。

wiki

在機器學習中，隨機森林是一個包含多個決策樹的分類器，並且其輸出的類別是由個別樹輸出的類別的眾數而定。 Leo Breiman和Adele Cutler發展出推論出隨機森林的演算法。而"Random Forests "是他們的商標。這個術語是1995年由貝爾實驗室的Tin Kam Ho所提出的隨機決策森林（random decision forests）而來的。這個方法則是結合Breimans的" Bootstrap aggregating "想法和Ho的" random subspace method " 以建造決策樹的集合。

好，簡單的理解就是利用隨機(重新抽樣)的方法種植出許多決策樹，樹的集合就是森林，接著從決策樹們的投票結果中選出票數最多的候選人作為本屆選舉結果。

#載入隨機樹森林package
#install.packages("randomForest")
library(randomForest)
set.seed(1117)

#(2)跑隨機樹森林模型
randomforestM <- randomForest(card ~ ., data = traindata, importane = T, proximity = T, do.trace = 100)
randomforestM

#錯誤率: 利用OOB(Out Of Bag)運算出來的
plot(randomforestM)

圖解0-500顆樹的錯誤率。

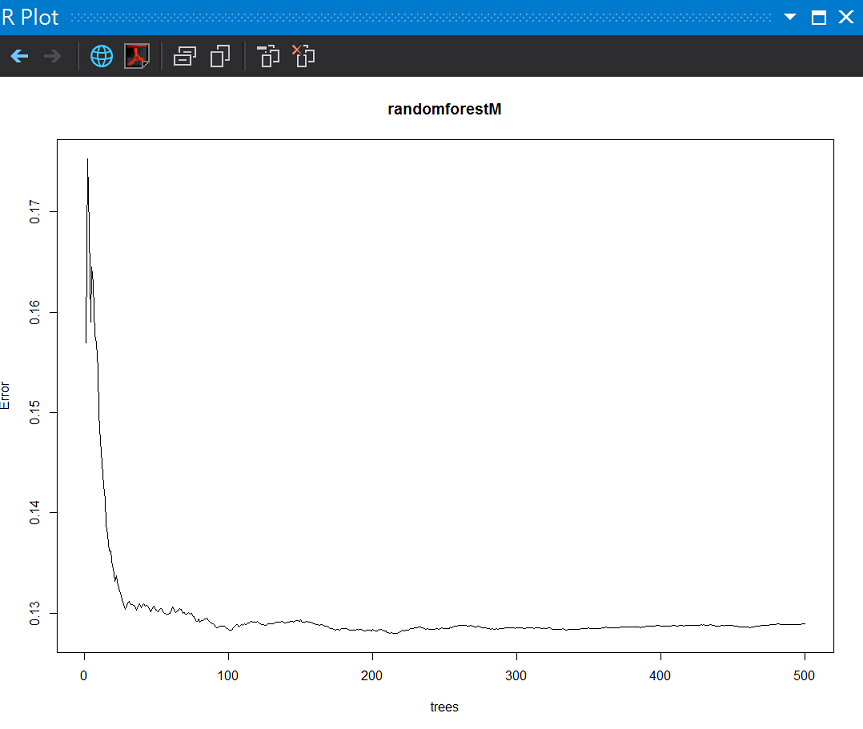
可以發現將分類樹放大綜合考慮後，前面20顆樹還在17%錯誤率，接著隨著森林的形成，就可以壓到13%錯誤率左右，我們可以使用團結力量大的方式來提升分類的成績。

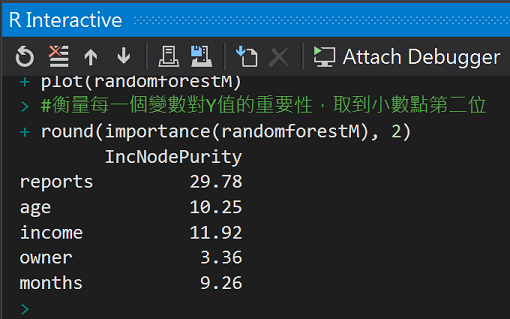
利用內建函式importance()來觀察每個變數x的重要性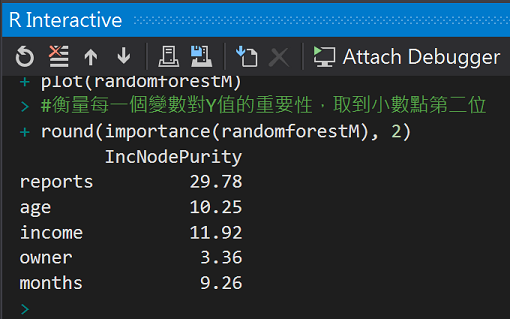

#衡量每一個變數對Y值的重要性，取到小數點第二位
round(importance(randomforestM), 2)

預測

#(3)預測
result <- predict(randomforestM, newdata = testdata)
result_Approved <- ifelse(result > 0.6, 1, 0)

#(4)建立混淆矩陣(confusion matrix)觀察模型表現
cm <- table(testdata$card, result_Approved, dnn = c("實際", "預測"))
cm

#(5)正確率
#計算核準卡正確率
cm[4] / sum(cm[, 2])

#計算拒補件正確率
cm[1] / sum(cm[, 1])

#整體準確率(取出對角/總數)
accuracy <- sum(diag(cm)) / sum(cm)
accuracy

正所謂獨木不成林，這邊我們將剛剛決策樹的結果與隨機森林比較，隨機森林的重新抽樣可以讓拒補件正確率提升了許多。