有人一定會想說：居然講這麼簡單的東西！這我一定會！

是沒錯拉！這東西基本上高中就會教到了，也就是印象中的回歸線阿相關係數等等章節.......
（聽到某些人尖叫崩潰的聲音......）
阿...........先不要擔心，雖然大家印象中的這些章節都含在統計當中，統計又是個讓大家頭痛的科目。
手算統計常常算錯又繁雜，統計又讀不懂他到底在講些甚麼.........

沒關係！今天會一次讓大家搞懂，沒有繁雜的計算，也沒有難懂的抽象。

基本上機器學習跟統計是很像的，機器學習講的是model而統計講的是hypothesis，也就是說機器學習會假設一個模型，接著去調整模型的參數讓他符合現有的資料，統計也是一樣，他會有一堆的hypothesis然後從中去挑一個最符合資料分布的。

線性模型

今天我們請到的模型是線性模型。

統計，到底在講甚麼！統計在講的其實是在講變數與變數之間的關係！
我們常常會去描述，像是有錢人的生活品質會比較好，窮人的生活品質會比較差，我們在邏輯上推論是這樣子的。
但是！真的是這樣嗎！

我們需要蒐集資料做調查，我們可能需要蒐集的是收入程度跟生活品質這兩個變數。
可是生活品質是個難以量化的抽象概念，我們或許可以讓人自己衡量自己的生活品質是0~10的幾分，或是我們可以去紀錄他每個月的支出是多少。
在前面的自我衡量中常常會受到心理的一些因素左右，像是明明生活品質不錯但是卻覺得自己不滿足，但是後者的衡量方法也有缺失的地方，像是可能他花了大把的鈔票在賭博或是買彩券，可是我們卻誤以為他的生活品質很好。

我們在收集資料的時候常常會有以上提到的這些bias或是產生一些誤差，這時候統計就會告訴我們，你需要的是機率，機率分布模型，像是常態分佈，就是我們常常用的模型之一，他可以處理誤差跟bias的部分。

那線性模型又是甚麼，線性模型是用來敘述兩個變數之間的關係是線性的，甚麼意思！？看下面這張圖就會知道了

也就是說，圖上的x軸跟y軸的關係可以畫成一條斜直線，而x軸跟y軸可以分別代表兩個不同的變數，像是我們剛剛提到的收入程度跟生活品質，當x的值越大，y就跟著越大，這個成長是線性的，線性的成長非常符合我們的邏輯跟直覺，所以我們很常使用他。

那我要怎麼找到那條線

大家可以稍微回憶一下我剛剛說的，機器學習當中有很多的model，我們需要從中去挑出一條最適合現有資料的model。
不過大家可能會說：我只有看到一條線(一個模型)而已阿！哪來很多模型？

不不不，你眼睛業障重！
那裏面有滿滿的......

阿！不對！是這張才對！

看到了嗎！我給了大家滿滿的斜直線！這就如同我前面提到的，我們需要從這堆模型當中挑一個出來，也就是對應不同的參數調整會成為不同的線。
那到底哪一條才是符合我們資料的分布情況的線呢？
讓我們先把線性模型的方程式寫出來

y = mx + b

其中我們的x跟y分別對應兩個變數，而m跟b就是我們要去找到的模型參數，其中m跟b都是實數，所以我們要搜尋的解空間是R^2，有無限多組解。

是的，我們要從無限多組解當中挑一組最適合的出來當成我們的解。

通常到這邊，數學課本會開始導公式，不過我要告訴大家概念，也就是說我們要找的那條線，其實是離每個點的距離最近的那條線，也就是這樣的概念

距離，我們也可以把它講成誤差，每個點不會百分之百剛好落在那條線上，當資料點跟線有誤差的時候我們需要找到誤差最小的線。

那我們要怎樣衡量誤差

通常我們認為的誤差會長這個樣子

sum(y' - y) = sum((mx + b) - y)

其中的y'是指我把x代入模型後，預估的y值，而x跟y則代表真正資料點的值，然後把每個資料點都計算過一遍之後把他們全部加起來。可是當中會有問題，因為有正有負，我有可能找到的是正很多跟負很多的值加起來等於零，可是這跟我們的預期不符，也無法表達我們距離的概念，所以我們會把它平方。

L(x, y) = sum( (y' - y)^2 ) = sum( ((mx + b) - y)^2 )

所以我們把它稱為Loss function，也就是衡量誤差的函數，所以到這邊我們已經把我們心裡所想的模型跟資料化成了可以計算的公式了。

我說那條線呢

講了這麼久，仍舊沒有把線給找到，倒是講了蠻多的概念的。

到現在基本上我們把要找到回歸線這件事公式化了，也就是試著將誤差減到最小。

那要怎麼減小誤差呢？

簡單的方法會用gradient descent，也就是梯度下降法，我們可以將我們的Loss function看成一個三維的空間，其中為了要達到誤差(z軸)最小，也就是相對在整個空間中最低的地方，我們去調整m跟b的值(分別是xy軸)來找到他。

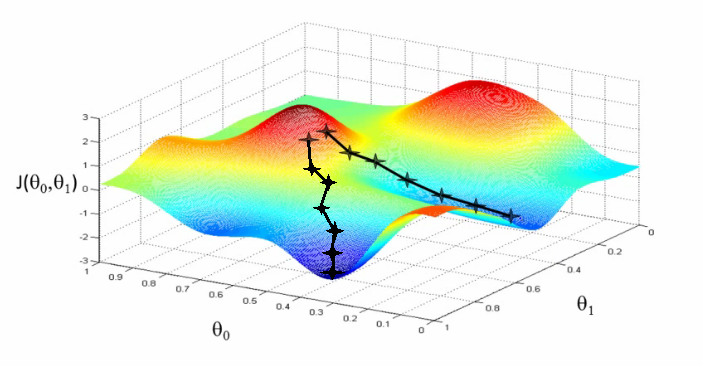
這邊就暫且不介紹梯度下降法了，可以留到以後再講。
總之，我們可以用gradient descent來找到我們要的那條線。

解構

那線性回歸當中有甚麼重要的東西呢

如果以機器學習的角度來說，它可以被拆解成幾個項目：模型、定義誤差並且公式化、最佳化演算法

模型也就是我們先前的假設拉~~~我們這邊用的是線性的模型。
定義誤差也是蠻重要的一個步驟，當你把誤差定義出來之後才有辦法將公式寫出來。這邊我們用的誤差是least square method，也就是最小平方法，很耳熟吧！
寫出公式之後就可以用演算法將它最佳化，找到最適合的解。這邊我們用的最佳化演算法是gradient descent。

基本上線性回歸指的是線性模型+最小平方法這回事，至於演算法要其他的也都可以，後續會繼續講線性回歸的其他方法。