這篇會介紹不同的activation function

Threshold function

這是在約50年前開始設計神經網路模型的時候提出來很簡單的activation function，他就是只要計算出來的值高於閾值就輸出1，否則就是0，不過放眼望去好像沒什麼人在用了阿XD
通常為了簡單，閾值會設成0。

Sigmoid function

這個activation function通常被用於分類問題的網路模型中，會輸出範圍介於[0, 1]，所以整體輸出恆正，而且嚴格遞增。由於feed-forward network通常會用back-propagation訓練，這個方法是gradient-based method，所以activation是可微的函數比較好計算，這邊介紹的activation function的微分都不會太難計算，而且簡化之後的算式都算漂亮，sigmoid function的微分是f'(x) = f(x)(1 - f(x))。

Hyperbolic tangent function

這也是個常用於分類問題的activation function，輸出範圍介於[-1, 1]，輸出範圍會有正有負，也是個嚴格遞增函數，他的微分是f'(x) = 1 - f^2(x)。實際應用上跟sigmoid function差不多，tanh收斂到1跟-1的速度比較快，所以容易學的比較慢一些，相對sigmoid function的學習表現也不是非常好，這兩個可以做初期測試用。

ReLU function

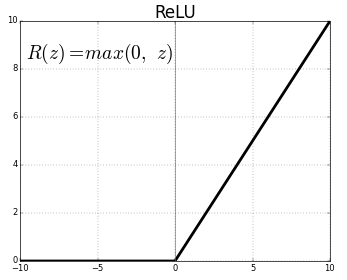
最近很紅的一個activation function，在分類問題上有非常好的表現，下界是0，沒有上界，也是個嚴格遞增函數，不過有時候要避免一個小問題，也就是一旦輸出變成0的話，那這個節點之後就會一直是0，那這樣個個節點就沒有作用了，一方面可以降低所需要的節點數，在收斂速度上會快很多。微分是，如果值有大於0的話就是1，沒有的話就是0。

Softplus function

基本上是一個連續版本的ReLU，也是用於分類問題上，不過表現上略遜ReLU一點。

Radial basis function

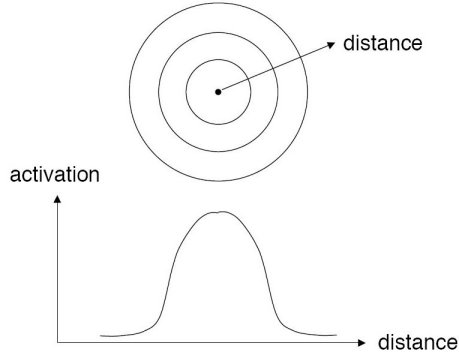
這是個很特別的activation function，用於RBF network，這個函數本身就是一個常態分佈，就我所知，在這個網路中他會去計算每個節點離某個中心點的距離，然後把距離通過這個activation function，這可以篩選出距離這個中心點近的點，所以他會對這些中心點敏感，可以設定不同的點讓網路去持續偵測這些點。