今天來補之前跳過沒講的gradient descent。

延續之前提到的，我們都會把一個模型加上某些measurement之後轉化成一個最佳化問題。
像是將線性模型加上Error measurement後，成為一個最佳化問題，而這個最佳化問題主要是要經由調整內部的參數，讓整個loss function的值最小。
如同這類問題就稱為最佳化問題。

Loss function

那要找出最佳化問題的解，就得看看這地形，長甚麼樣子。
通常loss function會有多個參數，但是在太高維度我們畫不出來，所以通常我們會觀察兩個參數的情況下 (分別為xy)，他的outcome會是如何。

梯度

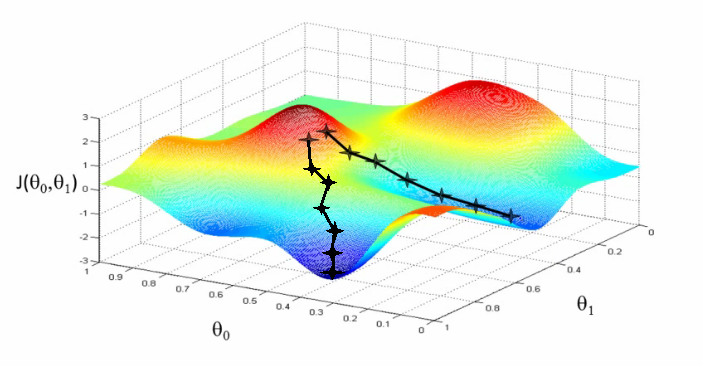
既然要找最小值，就意味著要往整個地形的最低點走，那我們就會想到要走現在這個位置最陡的那個方向下去。
所以這個演算法會去計算現在這個位置的梯度，然後往梯度最小的那個方向走，直到梯度為0為止。

為什麼是梯度呢？其實只是數學名詞而已，他其實就是斜率拉！
差別在於，當我們的函數只接受一個變數作為輸入的時候，我們會說斜率，他比較像是在一條直直的溜滑梯上，方向是固定的，當函數可以有多個變數的時候，我們會說梯度，他就像是在一個開放的山丘上，可以有不同的方向。

梯度下降

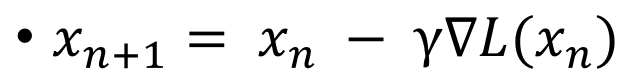
以上就是gradient descent的公式兼演算法拉~~~
x_n+1就是下一步的位置，x_n就是現在的位置，我們先看(倒三角)L(x_n)的地方，(倒三角)指的就是對某人取梯度的意思，所以在這邊就是去計算位於L(x_n)的梯度拉~~~

你問我L()是甚麼？難道我還沒說他是loss function嗎？
最後說明那個gamma，那代表的是我們往下走一步是多大步。有人稱他為learning rate，基本上值越大會越快到達終點，但是在某些狀況下他會不斷震盪喔。

細節

或許細心的人會有疑惑，在山坡的某一點上取梯度是甚麼意思？因為在一個立體空間中，我可以計算朝向不同地方的斜率，朝不同方向的話，斜率就會不一樣阿。

沒錯，在一個位置上有不同的方向導數，也就是真正斜率的意思，像是如果站在一個位置上測量南北向的斜率一定跟東西向的斜率不同，而梯度指的是各方向導數中最大的那個。

所以搭配前面的負號，表示著往斜率最大的反方向走的意思。

今天就到這邊吧！