Recommendations from known user/item features

現在的問題是，我們該如何給出推薦呢？

我們要藉由什麼方法去推測，一個人對沒看過電影的評價呢？

讓我們想像一下，我們對於每部電影和使用者都有一些特徵集合，比如下面的例子

以大佛普拉斯為例，我們其實無法精確的表示這一部電影屬於那一種電影，比方說愛情片也可以歸類在劇情片

所以想像電影v存在一個向量，它包含了多種的訊息

v = [劇情,愛情,動作,喜劇....]

大佛普拉斯 = [0.5, 0.1, 0, 2.5...]

有了這矩陣，我們就能知道電影有關的類型有那些，同樣的對於每一個使用者u，也建立一樣的矩陣，這個矩陣關係到的是使用者個人的喜好

我們假設Andes是一個沒有幽默感並且討厭喜劇的人

u = [劇情,愛情,動作,喜劇....]

Andes = [1.5, 10, 5, 0.1...]

而關於電影的向量我們稱為Rv而使用者則稱為Lu，有了這些訊息後我們要如何使用它呢？

直觀來看我們只要比較兩個向量即可得知，若是越一致表示該部電影越合你的胃口反之亦然

這個式子表示使用者u對未看過的電影v喜好程度的評估

接下來使用的方式跟評估兩個文件相似度一樣，以上面兩個例子為例

Rv1 = [0.5, 0.1, 0, 2.5...]
Lu1 = [1.5, 10, 5, 0.1...]

< Rv1 , Lu1 > = 0.5*1.5 + 0.1*10 + 0*5 + 2.5*0.1 = 2

假設有一個Lu2 = [1, 0, 3, 10]
Rv1 * Lu2 = 0.5*1 + 0.1*0 + 0*3 + 2.5*10 = 25.5

所以當我們要給出推薦時會怎麼做呢？我們只要對這個使用者與全部未觀賞過得電影做排列

按預測評價結果排序，那麼我們就可以推薦評價最高的那一個

有一點必須提醒，我們的評價應該是0~5之間(星星數)，25這個數字明顯暴錶，當然那是因為我們還沒加以限制，但這個結果仍不影響這個模型的效力

Predictions in matrix form

現在我們不再討論，如何將電影與使用者以某種方式結合起來，而是探討如何進行預測

這裡需要運用到一些線性代數的知識，當我們預測使用者u對於特定電影v的評價時

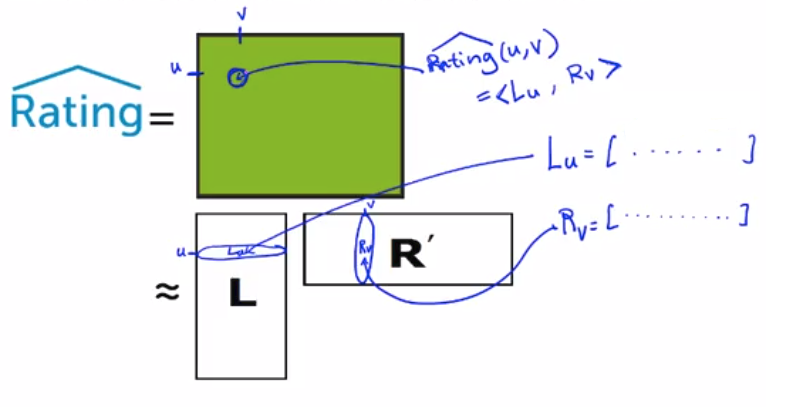
按照前面說過得，我們會得到Rv跟Lu，然後將其元素相乘，依照這個方法求得所有的使用者與電影的結果

最終我們可以得到一個完整的矩陣，矩陣裡面的每一個元素，都是特定Rv與特定的Lu的組合

Discovering hidden structure by matrix factorization

我們將所有使用者與電影做矩陣相乘，得到一個巨大的喜好預測矩陣

事實上我們是不知道這些資料的，相反的我們可以反過來想這個問題，接下來將嘗試估計R矩陣與L矩陣的值

當然這是建立在目前觀測到的評價來為每個使用者與電影估計它的特徵向量

而這些矩陣或者稱為主題向量的集合就是我們模型的參數

現在回到我們之前提過得回歸模型，對於已知的模型與相關的參數，如何有效從這些資料來推估這些參數

這邊的資料就是我們觀察到的評價

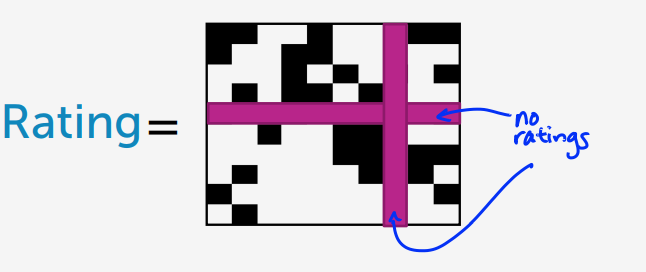
資料是什麼呢？就是那些黑色方塊，而參數就是使用者與電影的特徵

由觀察的評價來估計每一個參數，要估計L與R和結果矩陣，只能透過這些黑色方塊

在回歸模型中我們討論過殘值平方和，那時候討論的是一間房子它有一系列的特徵，這些特徵對應著權值

而那些權值就是我們的參數，我們由此來預測東西的價格，最後將預測與實際價格做比較

求出其差平方，並且將資料中的每間房子對應值相加，在這個例子中模型參數變成L與R

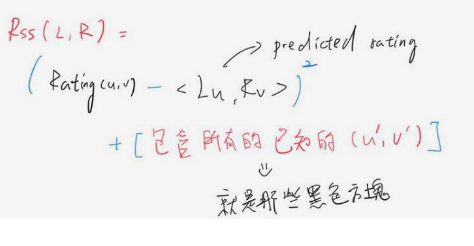
接下來用給定的L與R求出來觀察預測值，我們將觀察與評估之前對黑色格子所作的預測結果為何

現在評估L與R跟之前回歸係數的權值一樣

在這個例子，我們檢索了所有電影與使用者的特徵向量，最後找出一個參數組合

這個方法稱為 matrix factorization 模型

之所以這樣稱呼是因為，這裡將把矩陣做因式分解來逼近它

最後我們將得到的Rv-hat和Lu-hat來得到預測值(填補白色空格)

matrix factorization 確實是一個不錯的工具但是他還有一個限制，就是之前提過得 Cold-Start 問題

這個模型依舊無法解決，當有一個新使用者或新電影時該怎麼辦？

Bringing it all together: Featurized matrix factorization

基於回歸的方法我們只能夠有限的解決問題，另一方面在 matrix factorization 我們看到，我們可以捕捉到商品與使用者的關係，尤其是學習這些因素的特徵

我們有辦法找出一個綜合的方法？

重要的是我們能夠獲取的東西，像是文件內容、當前時間、使用者資訊、過去購買的紀錄

然後從 matrix factorization 中發現的特徵，它能夠得到一些行為相似的組別

比如：上PTT八卦板的宅宅們

直覺上當我們獲得一個沒有歷史購買紀錄的新使用者，我們將從其使用者資訊下手(年紀、性別...)

來預測他的得分，同樣的通過獲得那個使用者越來越多的資料，我們就可以加大 matrix factorization 的權重，在推薦的時候，選用它學到的特徵

這是一種非常普遍的混合模型，在 netflix 競賽中很常見

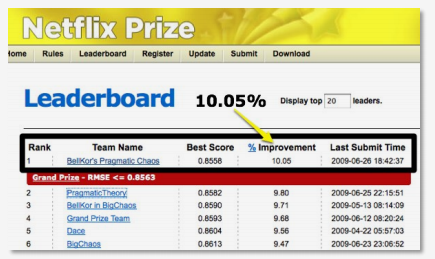
這是一個對使用者做出評價預測的比賽，誰可以幫 netflix 提供最精準的使用者分數預測

資料包含著:1億個不同使用者的觀影紀錄及評價幾乎有一萬八千部影視作品目標是對300萬則評價做出最高準確率的預測

領先的團隊幾乎用了上百個模型來達到這個水準

這種組合不同類型的解決方法，我們將在之後進行更多的討論

Reference:

• Machine Learning Foundations: A Case Study Approach 華盛頓大學在 coursera 上的公開課程，為本筆記追蹤的主要素材
• 課程投影片