transform的一個屬性：matrix(矩陣)

這個是很多人所懼怕的，因為沒有學過，或者學過不懂。
我會盡力以簡單的方式講給大家懂。

目前也在看svg，雖然還沒有看到跟矩陣有關係，
但是svg既然是向量檔，我想矩陣應該跑不掉，一定有關聯。

如果你是看到數學就頭暈的人，我會建議你還是要把它看完，

沒有人一開始就懂的，只是我比較聰明。-----Jason。

githubpage有範例可以玩

一.何為矩陣？

你可以把矩陣想成方陣思密達。

只是方陣裡面裝的是士兵，矩陣裡面裝的是數值。

複習一下
transform的其他四個屬性分布是translate(位移)、scale(縮放)、rotate(旋轉)、skew(傾斜)
其實transform只有一個重要數值，那就是matrix，
剩下的其實都是由特定的matrix去延伸的，
這四個數值是為了讓transform可以更簡單的被利用。

二.matrix表示法

transform: matrix(a,b,c,d,e,f);
什麼！？一堆參數，怎麼記得住？
不用怕，其實只是兩兩一組。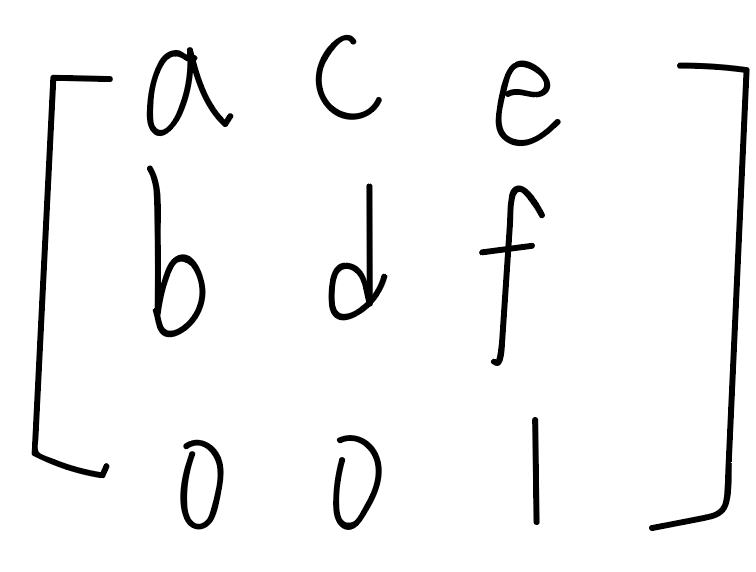

最後補上一列0 0 1。

三.何為矩陣的運算

矩陣的運算可想成捉對廝殺（相乘），
只有特定的我方士兵可以跟特定的敵方士兵對決，
按照各個顏色的箭頭，
第一個士兵跟第一個遇到的敵方士兵對打；第二個士兵跟第二個遇到的敵方士兵對打，以此類推。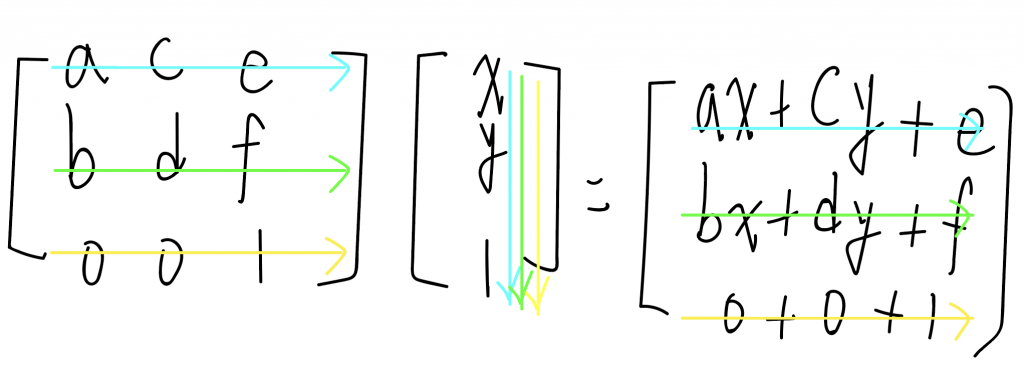

常常看Jump漫畫的人應該可以理解，

「這裏交給我！你快去找多佛朗明哥！」

「你就由我來對付，魯夫他可是要成為海賊王的男人」

或者

這種例外

而捉對廝殺（相乘）的結果也依序寫下來。
所以要怎麼去解釋這個運算式呢？
其實很簡單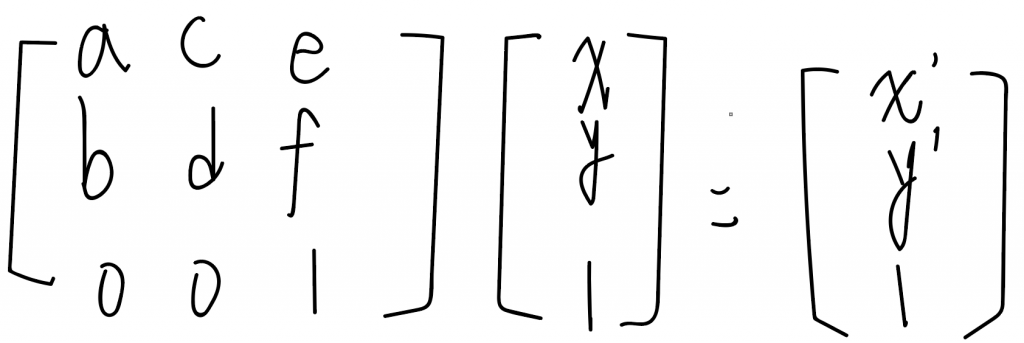

原本有一個座標為（x,y）的點經過一個矩陣運算後跑到(x',y')了。
其中x'=ax+cy+e; y'=bx+dy+f。

實例：當x=0,y=0
原點(x,y)=(0,0)
經過一個transform: matrix(1,,0,0,1,20,20);
x'=ax+cy+e=0+0+20=20; y'=bx+dy+f=0+0+20=20
新點(x',y')=(20,20)，
你會發現結果跟transform: tranlate(20px,20px);一樣。
再回去看看運算過程：
會發現matrix（沒空,去洗澡了,已讀不回,去睡了,水平位移距離,垂直位移距離)
所以translate(位移)只要管最後兩個參數就好(e,f)就好，
剩下的都不用管。
martix VS translate

縮放(scale)

聰明的你有發現方塊大小都沒有變嗎？
沒錯！
再回去看x'=ax+cy+e=; y'=bx+dy+f，
剛剛a=1；d=1，
如果matrix(1,,0,0,1,0,0)
會得到x'=x=; y'=y
我們改一下，a=2；d=2，
會得到x'=2x=; y'=2y。
（中文：後來的x座標是原來x座標的兩倍；後來的y座標是原來y座標的兩倍。）
如網頁範例。

martix VS scale

目前小複習
ad管縮放；ef管位移
接下來會比較難，三角函數來啦！！！！！！！！！！！！！
到這邊果斷放棄沒關係的。
不過如果你想要堅持是OK的！
這邊我就不介紹為什麼了，
這邊用記的吧！

旋轉(rotate)

其實我已經忘了旋轉矩陣怎麼來的，旋轉矩陣wiki
我自己只記得這樣，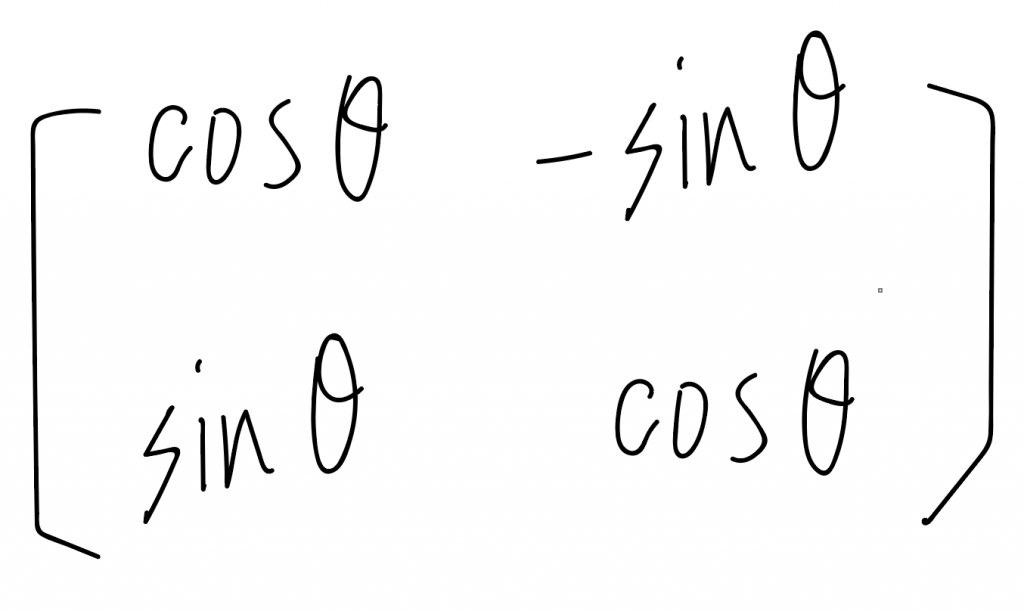

所以用matrix表示：
matrix(cosθ,sinθ,-sinθ,cosθ,0,0)。
很難記對吧！

用圖像記憶法：cs-sc

好吧！剛好我有用拼音：cs-sc可以寫成初三-上床
一次就記起來了

不過就rotate而言，matrix就不好用了，
因為rotate(θdeg)清楚明瞭，如果換成matrix(cosθ,sinθ,-sinθ,cosθ,0,0)
要計算值，以簡單的30deg為例：
transform:rotate(30deg);和transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);，
效果是一樣的。（拿出工程計算機吧！）

martix VS rotate

傾斜(skew)

剛剛還有兩個值沒有用到，那就是b和c，
不過是tanθ，
我的範例使用60°，tan60°=√3=1.73205080757
tanθ高中學的不多，真的無法深入介紹了。

martix VS skew

既然有translate、scale、rotate、skew，
要matrix做什麼呢？

目前我的想法是：高中還有鏡像矩陣、投影矩陣、什麼正交投影的...
感覺有機會可以實現！