Ref.: Classification

看到有人關注這系列文章實在很開心，但盡信書不如無書，全信我不如不要學ML。
建議多看多學其他的source，以免被單一資源給嚴重誤導。

今天這篇的預估學習時間：90分鐘。超多！！
頭都洗一半了，還是得寫下去。

以下先考慮分兩群，就是只有True或False
分多群的以後會再介紹

門檻值Thresholding

假設我們要預測是A (true)還是不是A (false)，最直接的想法就是給定一個機率p，P(A): 0.5<=p<=1, P(B): 0<=p<0.5。大於一半(0.5)的機率就是A，小於一半(0.5)的機率就是B。0.5就是我們的門檻值Threshold。換句話說，門檻值不一定要是0.5，可以是我們自己定義的數值。
這個數值是根據問題而定，慢慢tune出一個最適合的數值。但挑選門檻值又要小心，它可能會讓你true變false，想想你們的有多少註冊通知信跑到垃圾郵件就知道了。

True vs. False and Positive vs. Negative

原諒我沒翻這個，真假正負？是非真假？太難了。

定義好我們的Positive Class vs. Negative Class後，就能判斷預測出來的是真的還假的。OK，我比較喜歡這樣看Google給的表：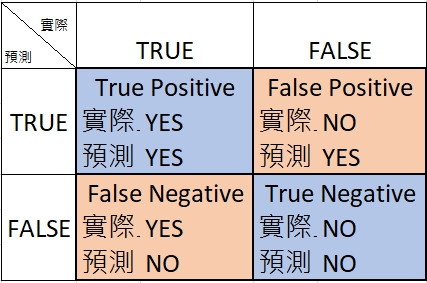

• True positive (TP): 真的有 (實際上就是有)
• False positive (FP): 假的有 (實際上就是沒有)
• False negative (FN): 假的沒有 (實際上就是有)
• True negative (TN): 真的沒有 (實際上就是沒有)

這幾個組合是接下來判斷model好壞的依據，Google提供放羊的小孩的例子滿親民的，假的就會讓人生氣。

正確率Accuracy

正確率Accuracy就是真的猜對的(TP+TN)除以所有猜的次數(TP+FP+FN+TN)。很不巧，正確率越高並不能代表越好，看看這個100 (1+1+8+90)個examples猜測的結果：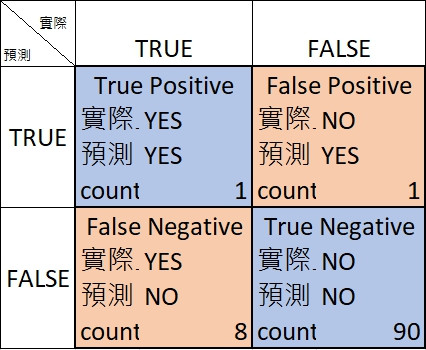

正確率 = (1+90)/100 = 0.91
看似挺高的，但問題是：

1. 它把很多實際是YES的都猜成NO ==> False positive (FN)很高。
2. 或者換一個觀察，所有的examples它幾乎都猜成NO，猜NO的機率高達(8+90)/100。
3. 再觀察一件事：實際上是NO的比例也很高(1+90)/100=91%。

很高的正確率通常會反應一些問題，像這邊提到的是class-imbalanced，Data set 中實際是True跟實際是False的數量差異太懸殊了。

Precision and Recall

Precision

What proportion of positive identifications was actually correct?
猜True(Positive)時有多少比例是正確猜對的

Precision = TP/(TP+FP)
上圖的例子是1/(1+1) = 0.5

Recall

What proportion of actual positives was identified correctly?
實際是對的而且也被識別出來(猜對)的比例有多少

Recall = TP/(TP+FN)
上圖的例子是1/(1+8) = 0.11，意思是有0.89的機率把True認成False的。

Precision-Recall 拉鋸戰

我重劃了Google的範例圖：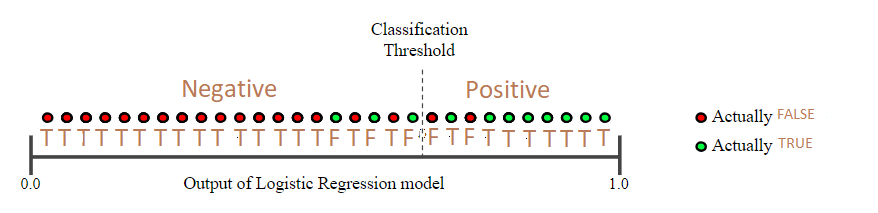

所有example根據predict probability由小排到大，再用threshold切一刀。左邊是Negative(猜False)，右邊是Positive(猜True)，搭配原本的example targets (actually TRUE or actually FALSE)，判斷到底猜對(T)還猜錯(F)。

• Threshold右邊綠點：實際是True，猜成True ==> TP，共 8 個
• Threshold右邊紅點：實際是False，猜成True ==> FP，共 2 個
• Threshold左邊綠點：實際是True，猜成False ==> FN，共 3 個
• Threshold左邊紅點：實際是False，猜成False ==> TN，共 17 個

因此這個範例來看
Precision = 8/(8+2) = 0.8
Recall = 8/(8+3) = 0.73

提高Threshold後...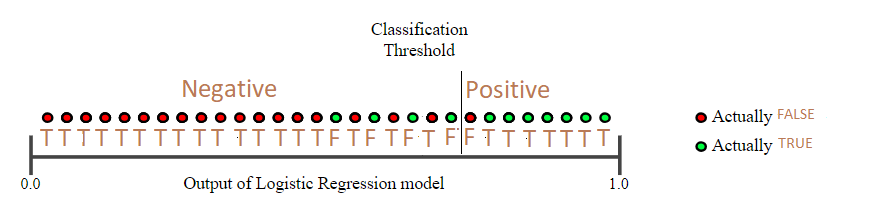

• Threshold右邊綠點：實際是True，猜成True ==> TP，共 7 個
• Threshold右邊紅點：實際是False，猜成True ==> FP，共 1 個
• Threshold左邊綠點：實際是True，猜成False ==> FN，共 4 個
• Threshold左邊紅點：實際是False，猜成False ==> TN，共 18 個

Precision = 7/(7+1) = 0.88
Recall = 7/(7+4) = 0.64

看看降低Threshold後呢?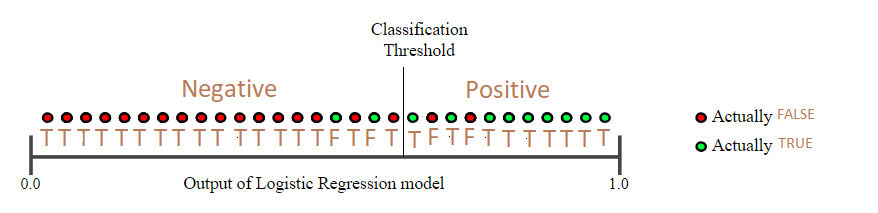

這個就再讓大家算看看囉(跟最後一個範例不太一樣!!)

好 今天先寫到這。剩下兩個部分留給明天吧！