Ref.: Logistic Regression

今天講跟機率、跟邏輯相關的迴歸分析，機率老實說我非常不OK，但還好看完不會碰到太深奧的機率理論。

對，機率就只是(AS IS)機率，她所說的就是有多少機率是(反過來說多少機率不是)。文中給了一個範例：

如果狗狗在半夜叫的機率 p(bark|night) 是0.05，那一年內晚上會叫的次數就是p(bark|night)*365 ~= 18次。

但很多情況我們只要預測是或否而已，我們需要的不是預測出一個很大很奇怪的數字，而是需要預測出0或1，這時候可以用到sigmoid function。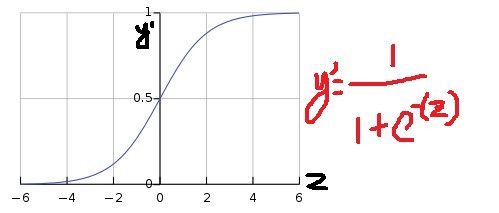

先看圖形，左逼近0，右逼近1。input z後所得到的 y'就會落在0~1之間。z離0越遠，y'越接近0或1。

z是什麼：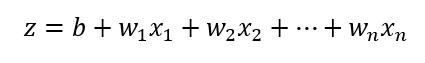

同時z也視為log-odd function，也就是 1的機率 / 0的機率：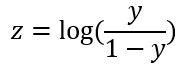

知道這麼多，套在model裡要怎麼辦呢？

Loss fun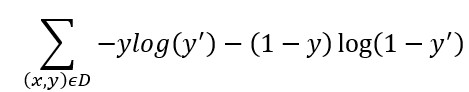ction for Logistic Regression

Log loss =
用在data D裡的examples (x, y) pair去算出 y'預測值及loss。

學過訊息理論(Information theory)的人對這個應該不陌生，有點像Entropy，而最小的loss function在最大的likelihood估計值的時候。

昨天講到的Regularization在這裡也很有用，因為越多次的估算會導致loss越接近0，所以這邊常用兩種方式去減少model complexity：

1. L_2 Regularization
2. 限制step提早結束。
   還有第三種之後會提到的L_1 Regularization

昨天說過少了Regularization會讓model overfit，這邊也是一樣。如果我們有一些每個example只出現一次的feature / crossed feature / id，這樣這個model會導致weight非常大，而且幾乎不會到loss為0。所以為了避免這個問題，一定要套一個Regularization的方法比較保險。