今天跟大家聊個簡單的問題：前綴極小值問題。

我們知道計算 min 可以在 O(n/p) 時間算得，但由於有 n 個值要輸出，一個顯然的平行算法可以在 O(n^2/p) 時間內被算出來。但絕大多數情形這個方法是沒有太大效率的，此時我們該怎麼辦呢？

注意到，我們並不太希望把輸出寫成 b[i] = min{b[i-1], a[i]}，原因是因為這樣會造成 b[i] 的計算必須取決於 b[i-1] 的值，這樣會難以平行。

事實上，我們可以把 a[1..n] 拆成 p 段，每一段先分別找出該段的最小值。這麼一來就可以再次利用這 p 個最小值找出 b[1..(n/p)*x] 的最小值。然後又可以根據這個算出正確的 b[i] 值，整體時間複雜度為 O(n/p + p)（如果追求極致，第二步我們可以再次遞迴下去解決同樣的子問題，所以利用前天的找最大值方法，這樣的時間複雜度是 O(n/p + log p / log log p)。）但總之我們可以達到高度的平行化，也就是說時間複雜度大約是 O(n/p)，比起原本的直接的演算法來說快了幾乎 p 倍。

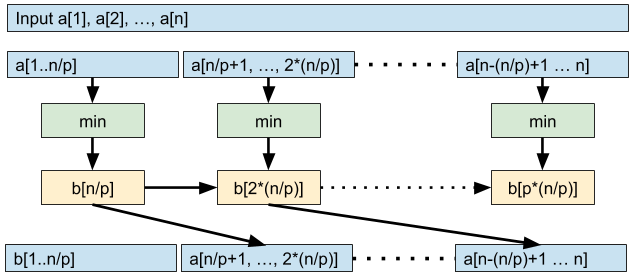
明天我們來看看這東西可以怎麼應用 :)

大家有興趣的話可以猜猜看XD