圖論上的拓撲排序

今天我們來討論討論在圖（Graph）上面的平行演算法。一個圖，是由一些節點（通常被稱為 Vertex 或 Node）以及一些連接兩個點之間的邊（Edge）所構成。一個有向圖（Directed Graph，又稱 Digraph）則是指所有的邊都被賦予了方向的圖。

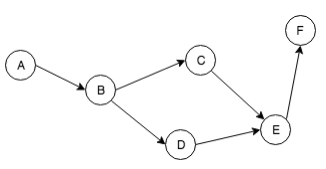
像上面這樣的圖，是沒有環（Cycle，又稱圈）的，這樣的有向圖我們把它稱為有向無環圖（Directed Acyclic Graph）。在這樣的圖上，我們不難觀察到：總是存在一個點，並沒有人指向它。我們如果依序挑出這樣的點，然後把這個點（與相連的邊）刪掉，就存在另一個點使得沒人指向它，然後可以重複以上動作，直到所有的點都被我們挑出來為止。

這樣把點挑出來的序列我們把它稱作「線性表列 Linear Ordering」，而找出任何一種線性表列的演算法被我們稱為「拓撲排序 Topological Sort」。一般來說實作上有 DFS 和 BFS 兩個方向，但這兩個方法其實在平行的世界裡不太管用，理由如下。

比方說，如果我們要用 BFS 方法平行化：找出所有 indeg = 0 的那些點。根據每一個處理器被分配到的點來說，indeg = 0 的點可能分佈地很不平均。我們不能把這些點放進 queue。如果把他們依序塞進一個 queue 裡面，就會在 queue 這邊造成順序的相依性，而喪失了平行化的優勢。

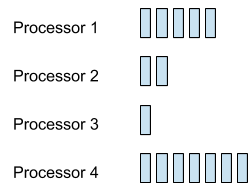
那該怎麼辦呢？我們可以利用另一種平行想法：讓每一個處理器固定負責一個範圍的點，比方說編號 1 負責編號 1~n/p 的點、編號 2 負責編號 n/p+1~2(n/p) 的點、依此類推。（這跟前天的前綴極小值的分法很像）然後我們在每個點上面儲存一個值 Rank[i] 代表「順位」。對於每一條邊 u → v，只要能夠滿足 按照這個順位由小到大把點都找出來，就完成了拓撲排序。（證明略）

一開始，所有「每人指向它的點」的順位都是 0。接下來，我們每一個回合考慮這些順位是 0 的點，然後考慮那些連出去的邊，並且更新連出去的邊的另一頭的 Rank 值為 1，這個更新是可以同時更新的（因為要更新對面的值永遠相同，所以不管誰先更新誰後更新，其值相同）。依此類推得出順位 0, 1, 2, …, D。

總共只要更新 D 個回合就好（D是長度最長的 path），而每一個回合的更新取決於該處理器負責的點的 out-degree 總和。所以總時間複雜度大約是 。

參考資料

https://academic.oup.com/comjnl/article-pdf/26/4/293/1072486/26-4-293.pdf
https://www.diva-portal.org/smash/get/diva2:927255/FULLTEXT01.pdf
https://pdfs.semanticscholar.org/f91a/350a7560e3d80a546852cbd66e492ceecfca.pdf