Day 13: 平行計算模型（六）Parallel Computation Model, Part 6 -- 分而治之法

2019 iT 邦幫忙鐵人賽

DAY 13

自我挑戰組

當傳統演算法遇到新的計算模型系列第 13 篇

2019鐵人賽

卡卡恩

2018-10-28 13:40:21

1482 瀏覽

分享至

Work Optimality

前天我們得到一個 $O(mn/p)$ 時間複雜度的最長嚴格遞增子序列演算法，其中 $n =$ 輸入序列長度、 $m =$ LIS 的長度、 $p =$ 處理器的數量。但這個演算法在 $p$ 很小的時候不是最優的。為了理解什麼是「好的平行化」，我們試圖給出一個客觀的定義 -- Work Optimality。

如果一個演算法 A 的非平行版本，其執行時間複雜度是 $T_1(n)$ ，而平行化後的演算法 PA 使用 $p$ 個處理器後的時間複雜度是 $T_p(n)$ 。我們說這個演算法 PA 相對於演算法 A 是 Work Optimal 的，若且唯若 $T_p(n) = O(T_1(n) / p)$ 。也就是說，給定 $p$ 個處理器以後，我們可以把總工作量平均分配到 $p$ 個處理器上。

回頭檢視 LIS 的演算法，傳統的 LIS 演算法，依序以二分搜尋法更新 L[1..m]，要花 $O(n \log n)$ 的時間。如果我們要找到 Work Optimal 的平行演算法，則要把我們的目標設立在 O(n log n / p) 的時間複雜度上。

之前在討論搜索問題的時候，我們知道遞迴呼叫是一種相依性，過深不是一件好事。但是如同N皇后問題一樣，如果我們可以分支出許多遞迴呼叫，那麼還滿適合拿來平行化的。

LIS 的分而治之法

而事實上，我們可以利用分而治之法解決 LIS 問題。要怎麼做呢？首先我們不妨假設輸入是一個 1~n 的排序（對原資料進行平行版的合併排序法可以作到 $O(n \log n/p)$ 時間。）接下來進行 Divide & Conquer 步驟：

Divide: 把輸入的序列分成 $\le n/2$ 以及 $> n/2$ 的兩部份
Conquer: 呼叫兩次遞迴，回傳兩個陣列 A[i] 以及 P[i]。其中 A[i] 表示以 i 為結尾的 LIS 長度為何，P[i] 表示其中一個以 i 為結尾的 LIS 他的前一個傢伙是誰。
Combine: 首先，因為我們把序列依照數值分成小數字和大數字兩種，所以小數字的 A 陣列值與 P 陣列值不需要做任何改變！至於大數字的部份，每一個大數字都可以連到它之前的任何一個小數字，只要長度是最長的就有機會接起來便得更長！我們把他想像成一個有向圖：對於每個數字 $x$ ，如果他是小數字 ( $x \le n/2$ )，我們就連一條邊 $x\to P[x]$ 。如果它是大數字 ( $x > n/2$ )，我們連兩條邊 $x\to P[x]$ 以及往前連到一個擁有最長 LIS 的小數字。意即：假設 $x$ 的位置是 i ，那麼定義 $best(i) = \arg\max_{j<i} A[j]$ ，而 $best(i)$ 的值是 y 的話，就連一條 x → y 的邊。

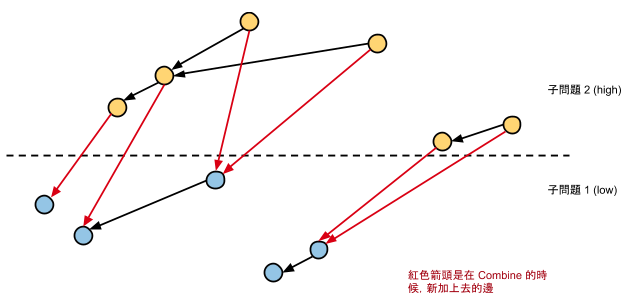
我們要做的事情就是在這張圖上更新 A 跟 P 兩個陣列的值。而這件事情相當於做拓撲排序。但是，為了作到 $O(m+n/p)$ 時間（而非昨天的 $O(m*(n/p))$ ），我們必須要把圖加上一些節點，並且改造成：每個節點的 in-degree 與 out-degree 至多都是 2。（這個圖的 out-degree 本身至多是 2，因為對一個 x，要嘛直接連出去一條，要嘛連出去兩條。）

在這樣的條件下，我們就可以用類似 BFS 的方式順利在 $O(m + \log n + n/p)$ 的時間內做出 A 和 P 兩個陣列了！

時間複雜度的分析

第 $k$ 層遞迴有 $2^k$ 個子問題，每一個子問題的大小大約是 $n/2^k$ 。因此，這層平行後所花費的總時間會是
$https://chart.googleapis.com/chart?cht=tx&chl=O(m%5Clog%20%5Cfrac%7Bn%2F2%5Ek%7D%7Bm%7D(2%5Ek%2Fp)%2Bn%2Fp)$ 。築層加總以後可以知道總花費時間會是 $https://chart.googleapis.com/chart?cht=tx&chl=O(m%5Clog%5E2%20%5Cfrac%7Bn%7D%7Bm%7D%20%2B%20n%5Clog%20n%2Fp)$ ，相當接近我們想要的 $O(n\log n/p)$ 了！而且若 $p=1$ 時還保證了最壞情形下時間仍是 $O(n\log n)$ ，很棒吧！

結論

我們得到一個 $https://chart.googleapis.com/chart?cht=tx&chl=O%5Cleft(m%5Clog%5E2%20%5Cfrac%7Bn%7D%7Bm%7D%20%2B%20%5Cfrac%7Bn%20%5Clog%20n%7D%7Bp%7D%5Cright)$ 的平行演算法，在 $p < \log n$ 時是 Work-Optimal 的。我的作法是改良自 2013 年的這篇 paper：https://www.sciencedirect.com/science/article/pii/S0020019013000902 。