前言

這次介紹，主成分分析英文名為Principal components analysis，簡稱為PCA，而這次一樣自己的觀點簡單的敘述，但還是會介紹一些數學公式，但其根本也能用最後結果簡單的說明。

投影向量

參考[1]介紹主要有兩種向量定義，一為代數定義，二為幾何定義。

代數定義

使用點對點相乘後加總，而這裡用矩陣的方式如下圖，A的反轉矩陣乘上B(原始數據為垂直列向量，所以將A做轉置)，結果與向量點對點相同。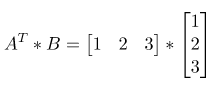

幾何定義

在歐幾里得定義點積[1]的公式為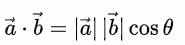，(來源:[1])，與上列代數定義兩者相等，而代數除上向量a*b長度後則可以得到角度。

純量投影

在歐幾里得當中垂直投影如下圖，向量a長度乘上cos theta，即可得到鄰邊，而鄰邊就是a投影在b的長度。

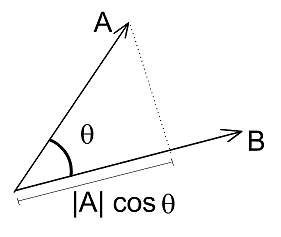
投影，來源:[1]。

PCA 公式

假設矩陣資料為A，投影矩陣為B，第一步先將每個垂直列零均值化(也能水平行，只是計算要反轉矩陣)，此步驟能將計算變異數的偏移值歸零，在二維意旨通過原點(能用直線公式理解為，y=ax + b，b為0)。這裡介紹兩種推導方式。

方法一

[2]的推導方式，沒有方法二較詳細推導，也簡單容易理解。

變異數

1.投影做內積公式。
在AdaBoost已經有介紹倒變異數這裡就跳過公式。在二維當中PCA降維利用了垂直投影到B向量並計算距離的方式(計算距離從二維變一維)，來代替目前的(x,y)表示方式，如下圖。紅色線為零均值化。

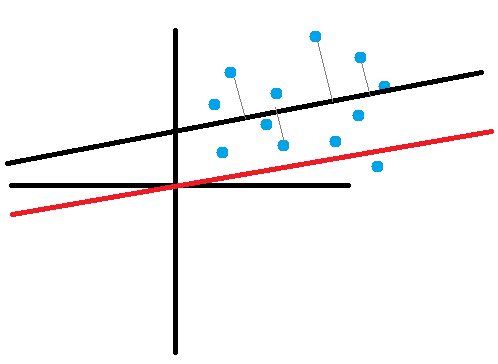
投影。

使用變異數來計算投影後差異，之後再找出向量B的最大極值(投影損失最少)，計算變異數的公式如下，(偏移量為0因做過零均值化)。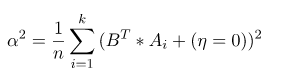

這裡使用矩陣所以公式如下圖，B轉置乘上A轉為水平行，所以右邊轉置，轉置後使用特性，(B轉置A)轉置=A轉置B詳細請看[4]。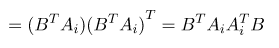

由上述可得知，公式最後為B零均值化的共變異數矩陣B轉置，共變異數矩陣在影像風格轉換也有介紹過(協方差矩陣)。

拉格朗日乘數

2.求投影到B時變異數最大公式(投影越大LOSS也相對較少)。
求最大化的條件為B^2為1(因條件模長=1)，如下圖。

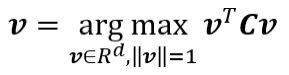
投影，來源:[2]。

求最大化可使用拉格朗日乘數來取得最佳解，可先看[5]的例子了解公式使用，有興趣也可以看推導。求最大值所以扣掉特徵如下方公式。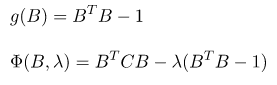

求微分，即可得到極值，可以看到這裡的極值就是共變異數矩陣的特徵值。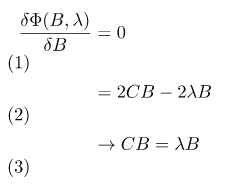

帶入原式，這裡可能特徵值為常量所以矩陣可交換，如下圖。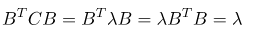

方法二

方法二是來自於[3]，這裡用更簡單的方式解釋，讓讀者能更加理解，而[3]是使用樣本標準差下去計算所以平均的分母都會-1。

樣本平均數向量

下面是證明樣本平均數公式(x - a)，a=m(樣本的平均)。如下圖所式。

1. 將原先公式x加上m，a減掉m(因為要證明所以將m代數方式帶入，並不會影響結果)。
2. 展開，當作矩陣所以有的乘法可轉為轉置矩陣。
3. 整理公式。

因假設a=m，所以後項都是0，最終解果(x - a)^2 = (x - m)^2，也就是所謂的離差[2]，離差AdaBoost有介紹過。

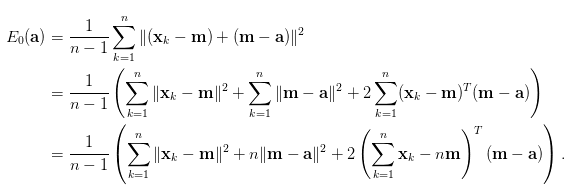
樣本平均數向量，來源:[3]。

均方誤差(方法一計算變異量方式)

此方法為了計算誤差，所以進行投射到一直線上面，而條件為，意指映射到模長=1。一開始都先將資料零均值化使得資料總和=0，而原先x可由映射後的權重來還原，公式為，，w為向量，c為純量，m和x的距離為|c|，這公式能理解出映射的簡易過程(能用直線公式來看待會更加容易理解)。
既然知道大概映射的過程，接著就是要求出c這個值，計算出誤差總和最小的即是我們要找的c，這時候就可以使用偏微分=0(變化等於0，在人工智慧章節有解釋過)，公式如下圖。

1. 將上述投影反推x公式扣掉原先x，使用均方誤差計算。
2. 整理公式，使得x-m再一起方便後續處理。
3. 展開公式。
   
   來源[3]。

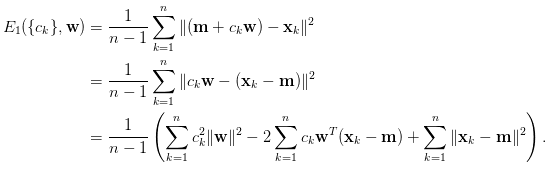
對c求偏微分(極小值，最小變化)。
1.求偏微分。
2.得出相等式子。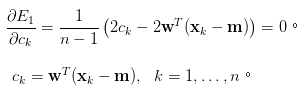

來源[3]。

將最小化相等公式帶入原先公式(取代x - m)。

1. 整理公式，並將c改為(x - m)。
2. 展開左邊sigma，並將w轉置*(x - m)位置互換，互換則兩者都要轉置。
3. 整理公式，使得中間為x零均值化的共變異數矩陣(對稱半正定性質，詳細說明可上維基)。
   
   來源[3]。

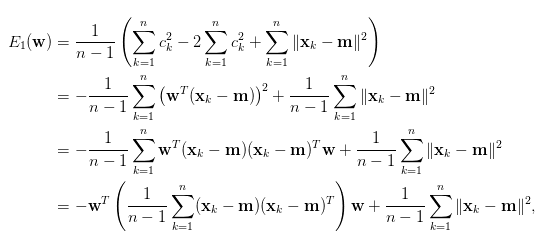
這裡的S即是共變異數矩陣，左邊sigma為扣掉均值總和=0。而[3]解釋數據集的總變異量 (即離差平方和)是一常數，所以最小化E(w)等價於最大化 w轉置SW。而這裡簡單解釋為，因E(w) = -w轉置SW，所以w轉置SW最大化等於最小化E(w)。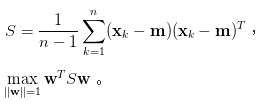

來源[3]。

求最大即帶入方法一所講到的拉格朗日乘數，求偏微分，即可得到S的對應公式。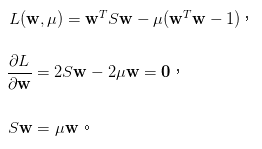

來源[3]。

解到這一步就可以得知w為特徵向量，所以只要求出共變異數矩陣的特徵向量和特徵值即可。

PCA降維

以上介紹的公式只需要將特徵值大小排序，再取出指定維度n的前n個特徵向量來做相乘。而最終所損失的量為，指定n維的特徵值和/全部特徵值和，如下圖。

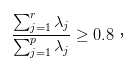
來源[3]。

PCA 實作

映射向量圖

首先來可視化映射向量，這裡有兩個紅色向量如下圖，可以想像為較長的是x映射，短的為y映射，因為x的值分散較大所以特徵值會較大，而y則較小。如下圖。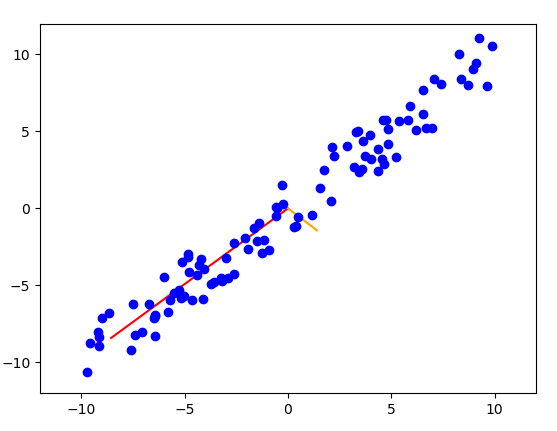

1. 建立資料。
2. 計算共變異數矩陣。
3. 得取特徵量和特徵向量(可以自己實作，但用原本作法會較慢，numpy有使用效率較高的公式，有點忘記使用那些了，有興趣可上網查詢)。
4. 畫出結果。

import numpy as np
import matplotlib.pyplot as plt

size = 100

data_x = np.random.uniform(-10.0, 10.0, size=(size, 1))
data_y = data_x - np.random.uniform(-2.0, 2.0, size=(size, 1))
data = np.hstack((data_x, data_y))

cov_matrix = np.cov(data,rowvar=0)
eig_val, eig_vec = np.linalg.eig(cov_matrix)

plt.plot([eig_vec[0, 0] * 12,0], [eig_vec[0, 1] * 12,0],color='red')
plt.plot([eig_vec[1, 0] * 2,0], [eig_vec[1, 1] * 2,0],color='orange')

plt.plot(data[:,0],data[:,1], 'o', color='blue')

plt.xlim(-12, 12)
plt.ylim(-12, 12)
plt.show()

PCA

接著實作PCA，使用上述的公式，最後並帶回計算是否會是原始資料。結果如下圖。

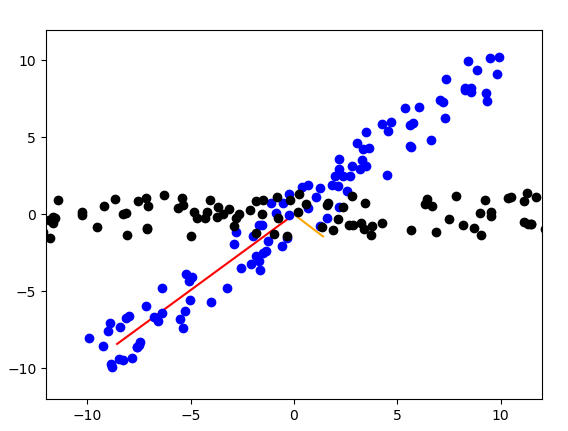
黑點為映射資料。

1. 創建資料。
2. 零均質化。
3. 計算共變異矩陣。
4. 計算特徵值和特徵向量。
5. 依照特徵值排序特徵向量。
6. 這裡選擇維度為2，所以eig_val_sort_indexs[:2]取出前兩個特徵向量做乘法(降一維改1)，結果即是映射後資料。
7. 依照上述公式，乘上反轉矩陣(推導時先乘矩陣再乘上原始矩陣，主要看資料是行還是列)，m+cw，c=w轉置*(資料零均值)，即是原先數據。

import numpy as np
import matplotlib.pyplot as plt

def zero_mean(data):
    mean = np.mean(data, axis=0)
    zero_data = data - mean
    return zero_data

size = 100

data_x = np.random.uniform(-10.0, 10.0, size=(size, 1))
data_y = data_x - np.random.uniform(-2.0, 2.0, size=(size, 1))
data = np.hstack((data_x, data_y))

zero_data = zero_mean(data)
cov_data = np.cov(zero_data, rowvar=0)
eig_val, eig_vec = np.linalg.eig(cov_data)
eig_val_sort_indexs = np.argsort(-eig_val)
eig_vec_sort = eig_vec[:,eig_val_sort_indexs[:2]]
mapping_data =np.dot(zero_data, eig_vec_sort) 

print(zero_data)
print(np.dot(mapping_data, eig_vec_sort.T))

plt.plot([eig_vec[0, 0] * 12,0], [eig_vec[0, 1] * 12,0],color='red')
plt.plot([eig_vec[1, 0] * 2,0], [eig_vec[1, 1] * 2,0],color='orange')
plt.plot(zero_data[:,0],zero_data[:,1], 'o', color='blue')
plt.plot(mapping_data[:,0],mapping_data[:,1], 'o', color='black')
plt.xlim(-12, 12)
plt.ylim(-12, 12)
plt.show()

總結

方法二的方法很詳細，最後推導得知w為特徵向量，最後總結出簡單的解釋。(解釋只是換個想法，實際上都要用以上數學來解釋，若上述推導能理解，這裡能跳過)。

1. 將資料零均質化，解釋為在二維中為了將特徵線通過原點，意旨任何資料都是通過原點，類似正規化。
2. 共變異數矩陣，解釋為在二維中計算x和y之間的離散數值。
3. 計算出離散數值特徵，解釋為在二維中x和y兩者的影響哪個較大，並可得到兩者的獨立特徵向量。
4. 資料乘上特徵向量，解釋為在二維中在獨立的向量當中是如何表示。

結語

在很久之前就聽過PCA，但每次都是看看，這次終於有機會將它完成，接著有時間還會繼續介紹各種算法，可能有的解釋並不是很好，但這主要是自己往後回來看原理能快速理解，請多包涵。有問題或錯誤歡迎糾正討論。

參考文獻

[1]維基百科(2019) 內積 from: https://zh.wikipedia.org/wiki/%E7%82%B9%E7%A7%AF(2019.05.20)
[2]Tommy Huang(2018) 機器/統計學習:主成分分析(Principal Component Analysis, PCA) from: https://medium.com/@chih.sheng.huang821/%E6%A9%9F%E5%99%A8-%E7%B5%B1%E8%A8%88%E5%AD%B8%E7%BF%92-%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90-principle-component-analysis-pca-58229cd26e71
[3]ccjou(2013) 主成分分析 | 線代啟示錄 form: https://ccjou.wordpress.com/2013/04/15/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90/
[4]ccjou(2013) 主成分分析 | 轉置矩陣的意義 form:https://ccjou.wordpress.com/2010/05/20/%E8%BD%89%E7%BD%AE%E7%9F%A9%E9%99%A3%E7%9A%84%E6%84%8F%E7%BE%A9/
[5]維基百科(2019) 拉格朗日乘數 from: https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0#%E8%AF%81%E6%98%8E
[6]https://upmath.me/