這次使用了之前介紹的CNN模型下去修改。主要參考[1]李弘毅老師的影片(內容圖文並茂),和[3]是屬於比較少圖片說明,但兩者其實大同小異,如果喜歡看公式可直接看[3],喜歡圖片解講可看[1]。
假設,是輸入資料的分布,但我們無法得知實際的資料分布,而假設
是一個任意函數來近似
,所以必須找到最大theta參數。這裡使用[1]圖片來解釋。
1.將機率相乘得到產生的機率,取log轉為指數。
2.指數可變為相加方便處理。
3.轉為期望,而上述其實與max為產生出x機率乘上
意思是一樣的。
4.轉為連續機率分布,再減上,這並不會影響結果,因為
是已知分布且固定的,可視為常數。
5.轉為KL散度,第三和四步驟能說是為了轉為KL分布計算。所以minKL散度(計算的KL為負數轉正求min)即是max原式。
在上一章VAE講到KL散度就是再度量兩者分布,其實也能直接寫出第五步驟解釋要度量兩者分布。
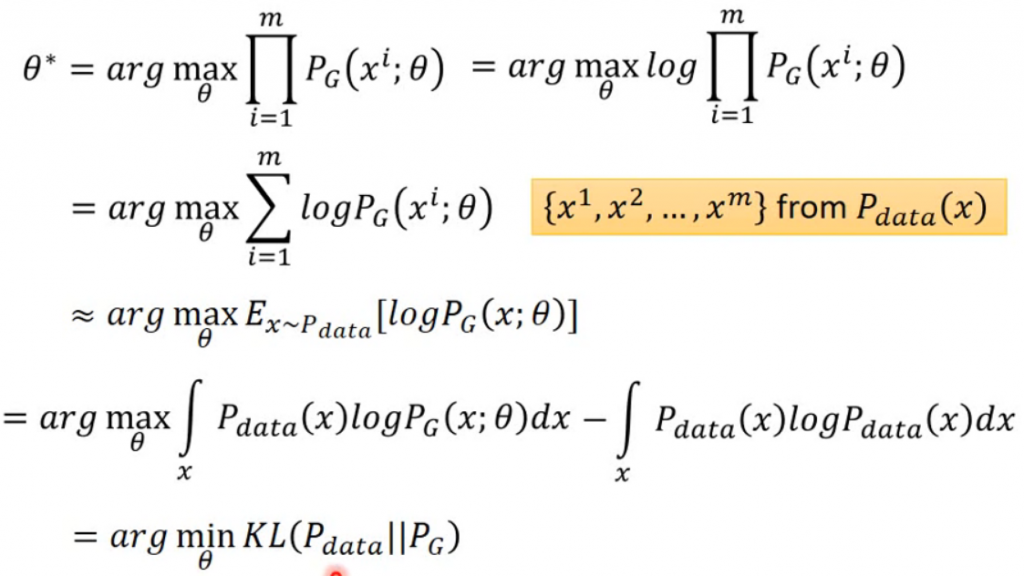
來源[1]。
這想法是可行的,在VAE講過在高維度當中要求出theta還是很難的,然而GAN利用最後計算出的結果來衡量。定義loss公式如下。
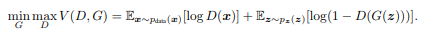
來源[2]。
以直觀角度來看,對於Discriminator就是讓原先資料辨識結果越高越好並且生成資料辨識越低越好,反知對於Generator就是讓生成資料辨識越高越好(原先資料辨識不影響)。
接著使用數學證明上述公式為何能當作loss。
首先將Discriminator最大化,而做這一步就能很明顯知道為何這式子可當loss。
1.當max D時,固定住G則會變為第一式。
2.轉為連續機率。
3.整理公式。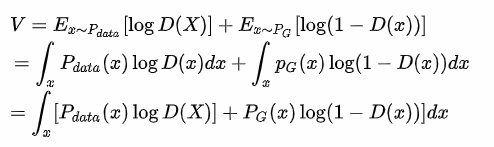
來源[3]。
假設、
則要最大化的公式如下。
來源[3]。
1.將a和b帶入。
2.對D求偏微分(log偏微分公式帶入),偏微分即是求出最大化。
3.整理公式。
4.將a和b帶回原先的分布。
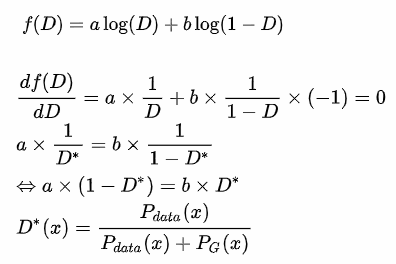
來源[3]。
1.將最大化D帶入原式,右邊1-D所以分子扣掉Pdata剩下Pg。
2.將分子分母除以2,因是常數並不影響。
3.將兩邊分子的1/2提到最前面,則結果會變為2個KL,而這兩個KL其實就是JS散度(也能說是對稱性KL),簡單來說就是一個計算分布差異的公式。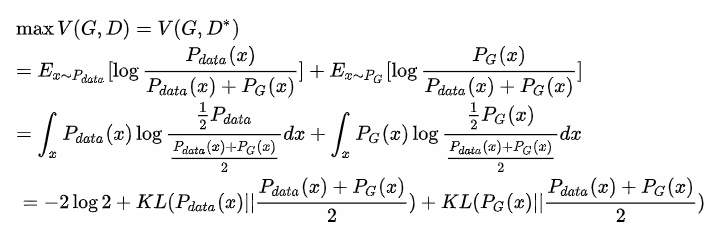
來源[3]。
而前面的-2log2是常數可以忽略,所以由此得知max D就是使用JS散度計算,這樣就知道loss是有意義的。
而Min G,則只需要對,因dG與左邊無關可忽略。而這裡要注意的是[2]提到不要最小化
,而是最大化
,如下圖。

來源[2]。
在[1]也有說明,其實主要是訓練時梯度下降的關西,最小化一開始會下降很慢,而最大化一開始則不會。如下圖。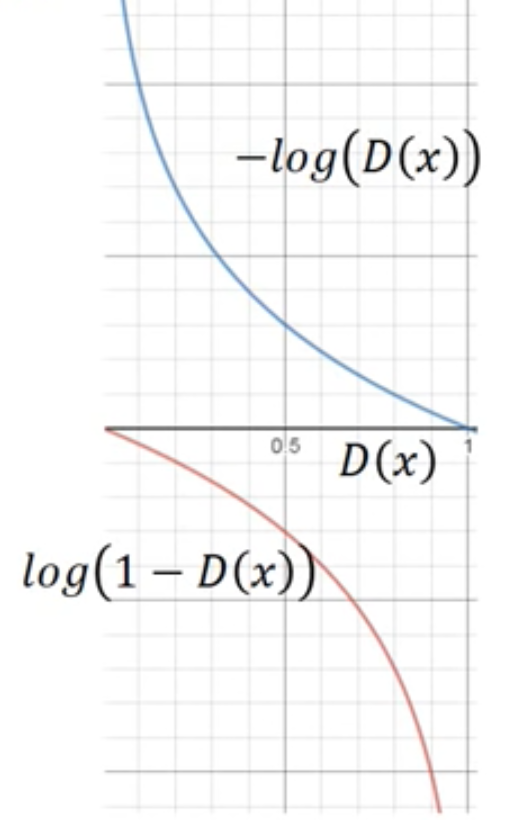
來源[1]。
對於和
我們是不知道真實分布,所以我們只能產生出圖片帶入計算。也就是真實圖片與Generator圖片帶入Discriminator計算log的平均。
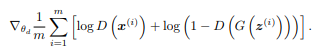
來源[1]。
使用之前CNN講解的程式下去修改。訓練需要較久時間,所以只使用50筆資料測試。
learning_rate: 學習率。
batch_size: 批次訓練數量。
train_times: 訓練次數。
train_step: 驗證步伐。
D_param: discriminator網路層所有相關權重,為了更新用。
G_param: generator網路層所有相關權重,為了更新用。
discriminator_conv: discriminator捲基層數量。
discriminator_output_size: discriminator輸出數量。
generator_input_size: generator輸入數量。
generator_conv: generator捲基層數量。
generator_output_size: generator輸出數量。
learning_rate = 0.0001
batch_size = 10
train_times = 100000
train_step = 1
D_param = []
G_param = []
# [filter size, filter height, filter weight, filter depth]
discriminator_conv1_size = [3, 3, 1, 11]
discriminator_conv2_size = [3, 3, 11, 13]
discriminator_hide3_size = [7 * 7 * 13, 1024]
discriminator_output_size = 1
generator_input_size = 20
generator_conv1_size = [3, 3, 1, 13]
generator_conv2_size = [3, 3, 13, 11]
generator_hide3_size = [generator_input_size * 11, 1024]
generator_output_size = 28 * 28
全鏈結層使用
def layer_batch_norm(x, n_out, is_train):
beta = tf.get_variable("beta", [n_out], initializer=tf.ones_initializer())
gamma = tf.get_variable("gamma", [n_out], initializer=tf.ones_initializer())
batch_mean, batch_var = tf.nn.moments(x, [0], name='moments')
ema = tf.train.ExponentialMovingAverage(decay=0.9)
ema_apply_op = ema.apply([batch_mean, batch_var])
ema_mean, ema_var = ema.average(batch_mean), ema.average(batch_var)
def mean_var_with_update():
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean), tf.identity(batch_var)
mean, var = tf.cond(is_train, mean_var_with_update, lambda:(ema_mean, ema_var))
x_r = tf.reshape(x, [-1, 1, 1, n_out])
normed = tf.nn.batch_norm_with_global_normalization(x_r, mean, var, beta, gamma, 1e-3, True)
return tf.reshape(normed, [-1, n_out])
捲積層使用
def conv_batch_norm(x, n_out, train):
beta = tf.get_variable("beta", [n_out], initializer=tf.constant_initializer(value=0.0, dtype=tf.float32))
gamma = tf.get_variable("gamma", [n_out], initializer=tf.constant_initializer(value=1.0, dtype=tf.float32))
batch_mean, batch_var = tf.nn.moments(x, [0,1,2], name='moments')
ema = tf.train.ExponentialMovingAverage(decay=0.9)
ema_apply_op = ema.apply([batch_mean, batch_var])
ema_mean, ema_var = ema.average(batch_mean), ema.average(batch_var)
def mean_var_with_update():
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean), tf.identity(batch_var)
mean, var = tf.cond(train, mean_var_with_update, lambda:(ema_mean, ema_var))
normed = tf.nn.batch_norm_with_global_normalization(x, mean, var, beta, gamma, 1e-3, True)
mean_hist = tf.summary.histogram("meanHistogram", mean)
var_hist = tf.summary.histogram("varHistogram", var)
return normed
捲積層
這裡多了type去判斷是哪個神經網路的參數。活化函數使用relu。
def conv2d(input, weight_shape, type='D'):
size = weight_shape[0] * weight_shape[1] * weight_shape[2]
weights_init = tf.random_normal_initializer(stddev=np.sqrt(2. / size))
biases_init = tf.zeros_initializer()
weights = tf.get_variable(name="weights", shape=weight_shape, initializer=weights_init)
biases = tf.get_variable(name="biases", shape=weight_shape[3], initializer=biases_init)
conv_out = tf.nn.conv2d(input, weights, strides=[1, 1, 1, 1], padding='SAME')
conv_add = tf.nn.bias_add(conv_out, biases)
conv_batch = conv_batch_norm(conv_add, weight_shape[3], tf.constant(True, dtype=tf.bool))
output = tf.nn.relu(conv_batch)
if type == 'D':
D_param.append(weights)
D_param.append(biases)
elif type == 'G':
G_param.append(weights)
G_param.append(biases)
return output
全鏈結層
這裡多了type去判斷是哪個神經網路的參數。和activation能選擇不同的活化函數。
def layer(x, weights_shape, activation='relu', type='D'):
init = tf.random_normal_initializer(stddev=np.sqrt(2. / weights_shape[0]))
weights = tf.get_variable(name="weights", shape=weights_shape, initializer=init)
biases = tf.get_variable(name="biases", shape=weights_shape[1], initializer=init)
mat_add = tf.matmul(x, weights) + biases
#mat_add = layer_batch_norm(mat_add, weights_shape[1], tf.constant(True, dtype=tf.bool))
if activation == 'relu':
output = tf.nn.relu(mat_add)
elif activation == 'sigmoid':
output = tf.nn.sigmoid(mat_add)
elif activation == 'softplus':
output = tf.nn.softplus(mat_add)
else:
output = mat_add
if type == 'D':
D_param.append(weights)
D_param.append(biases)
elif type == 'G':
G_param.append(weights)
G_param.append(biases)
return output
這裡與之前CNN神經網路雷同。而這裡我選擇使用sigmoid活化函數(有些使用tensorflow的cross...函數去做可不用)為了讓loss的log能運算。
def discriminator(x):
x = tf.reshape(x, shape=[-1, 28, 28, 1])
with tf.variable_scope("discriminator", reuse=tf.AUTO_REUSE):
with tf.variable_scope("conv1", reuse=tf.AUTO_REUSE):
conv1_out = conv2d(x, discriminator_conv1_size)
pool1_out = max_pool(conv1_out)
with tf.variable_scope("conv2", reuse=tf.AUTO_REUSE):
conv2_out = conv2d(pool1_out, discriminator_conv2_size)
pool2_out = max_pool(conv2_out)
with tf.variable_scope("hide3", reuse=tf.AUTO_REUSE):
pool2_flat = tf.reshape(pool2_out, [-1, discriminator_hide3_size[0]])
hide3_out = layer(pool2_flat, discriminator_hide3_size, activation='softplus')
#hide3_drop = tf.nn.dropout(hide3_out,keep_drop)
with tf.variable_scope("output"):
output = layer(hide3_out, [discriminator_hide3_size[1], discriminator_output_size], activation='sigmoid')
return output
這裡與之前的CNN也雷同,這裡第一行reshape則是上述參數的generator輸入。
def generator(x):
x = tf.reshape(x, shape=[-1, generator_input_size, 1, 1])
with tf.variable_scope("generator", reuse=tf.AUTO_REUSE):
with tf.variable_scope("conv1", reuse=tf.AUTO_REUSE):
conv1_out = conv2d(x, generator_conv1_size, type='G')
with tf.variable_scope("conv2", reuse=tf.AUTO_REUSE):
conv2_out = conv2d(conv1_out, generator_conv2_size, type='G')
with tf.variable_scope("hide3", reuse=tf.AUTO_REUSE):
conv2_flat = tf.reshape(conv2_out, [-1, generator_hide3_size[0]])
hide3_out = layer(conv2_flat, generator_hide3_size, activation='softplus', type='G')
with tf.variable_scope("output", reuse=tf.AUTO_REUSE):
output = layer(hide3_out, [generator_hide3_size[1], generator_output_size], activation='sigmoid', type='G')
return output
損失函數這裡將它分為兩個,一個用來訓練Discriminator一個用來訓練Generator,將上述推導公式帶入即可。
def discriminator_loss(D_x, D_G):
loss = -tf.reduce_mean(tf.log(D_x + 1e-12) + tf.log(1. - D_G + 1e-12))
loss_his = tf.summary.scalar("discriminator_loss", loss)
return loss
def generator_loss(D_G):
loss = -tf.reduce_mean(tf.log(D_G + 1e-12))
loss_his = tf.summary.scalar("generator_loss", loss)
return loss
這裡驗證主要存為圖片觀看。
def image_summary(label, image_data):
reshap_data = tf.reshape(image_data, [-1, 28, 28, 1])
tf.summary.image(label, reshap_data, batch_size)
def accuracy(G_z):
image_summary("G_z_image", G_z)
def discriminator_train(loss, index):
return tf.train.AdamOptimizer(learning_rate=0.0001, beta1=0.9, beta2=0.999, epsilon=1e-12).minimize(loss, global_step=index, var_list=D_param)
def generator_train(loss, index):
return tf.train.AdamOptimizer(learning_rate=0.0001, beta1=0.9, beta2=0.999, epsilon=1e-12).minimize(loss, global_step=index, var_list=G_param)
這裡為了讓Generator快速產生結果,而訓練多次。然而訓練過程有時會不錯有時會很糟糕,能感受的到GAN是個不穩定模型。
if __name__ == '__main__':
# init
mnist = input_data.read_data_sets("MNIST/", one_hot=True)
input_x = tf.placeholder(tf.float32, shape=[None, 784], name="input_x")
input_z = tf.placeholder(tf.float32, shape=[None, generator_input_size], name="input_z")
# predict
D_x_op = discriminator(input_x)
G_z_op = generator(input_z)
D_G_op = discriminator(G_z_op)
# loss
discriminator_loss_op = discriminator_loss(D_x_op, D_G_op)
generator_loss_op = generator_loss(D_G_op)
# train
discriminator_index = tf.Variable(0, name="discriminator_train_time")
discriminator_train_op = discriminator_train(discriminator_loss_op, discriminator_index)
generator_index = tf.Variable(0, name="generator_train_time")
generator_train_op = generator_train(generator_loss_op, generator_index)
# accuracy
accuracy(G_z_op)
# graph
summary_op = tf.summary.merge_all()
session = tf.Session()
summary_writer = tf.summary.FileWriter("log/", graph=session.graph)
init_value = tf.global_variables_initializer()
session.run(init_value)
saver = tf.train.Saver()
sample_z = np.random.uniform(-1., 1., (mnist.train.num_examples, generator_input_size))
D_avg_loss = 1.
while D_avg_loss > 0.001:
total_batch = 1
for i in range(total_batch):
minibatch_x = mnist.train.images[i * batch_size: (i + 1) * batch_size]
data = sample_z[i * batch_size: (i + 1) * batch_size]
session.run(discriminator_train_op, feed_dict={input_x: minibatch_x, input_z: data})
D_avg_loss = session.run(discriminator_loss_op, feed_dict={input_x: minibatch_x, input_z: data})
for time in range(train_times):
D_avg_loss = 0.
G_avg_loss = 1.1
total_batch = 1
for i in range(total_batch):
minibatch_x = mnist.train.images[i * batch_size: (i + 1) * batch_size]
data = sample_z[i * batch_size: (i + 1) * batch_size]
session.run(discriminator_train_op, feed_dict={input_x: minibatch_x, input_z: data})
D_avg_loss = session.run(discriminator_loss_op, feed_dict={input_x: minibatch_x, input_z: data})
for k in range(7 + 5 * int(time / 500)):
session.run(generator_train_op, feed_dict={input_x: minibatch_x, input_z: data})
G_avg_loss = session.run(generator_loss_op, feed_dict={input_x: minibatch_x, input_z: data})
last_loss = 99.
over_time = 0
while G_avg_loss > 1. and over_time < 10:
if last_loss < G_avg_loss:
over_time += 1
last_loss = G_avg_loss
session.run(generator_train_op, feed_dict={input_x: minibatch_x, input_z: data})
G_avg_loss = session.run(generator_loss_op, feed_dict={input_x: minibatch_x, input_z: data})
if ((total_batch * time) + i + 1) % train_step == 0:
data = sample_z[0:batch_size]
image_summary("G_z_image", session.run(G_z_op, feed_dict={input_z: data}))
summary_str = session.run(summary_op, feed_dict={input_x: mnist.validation.images[:batch_size], input_z: data})
summary_writer.add_summary(summary_str, session.run(generator_index))
print("train times:", ((total_batch * time) + i + 1),
" D_avg_loss:", session.run(discriminator_loss_op, feed_dict={input_x: minibatch_x, input_z: data}),
" G_avg_loss:", session.run(generator_loss_op, feed_dict={input_x: minibatch_x, input_z: data}))
session.close()
訓練一下即可看到成果(1~10分)。實際訓練會隨機產生出新的亂數,這裡單純測試所以固定產生,加快看到結果。



一開始嘗試直接使用全數據和亂數訓練,但訓練時間太長,且也沒有一個值判斷目前的訓練情況,而訓練值也不好調整,訓練起來與先前的網路相比算是一大挑戰,但這幾年許多人將GAN模型修改,而Wasserstein GAN(WGAN)是其中一個突破,能得知目前的結果是好還是壞,未來有機會還會介紹WGAN,若文章有誤歡迎糾正討論。
[1] 李宏毅(2018) GAN Lecture 4 (2018): Basic Theory from: GAN Lecture 4 (2018): Basic Theory
[2]Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio, "Generative Adversarial Nets" arXiv:1406.2661, Jun. 2014.
[3] Sherlock(2018). GAN的数学推导 from: https://zhuanlan.zhihu.com/p/27536143
