很多現實生活中的問題都跟時間有關，也可說是時間的函數，例如空間飛行、化學反應、種族增長、投資、汙染控制和運動控制等，都是廣泛應用動態模型的領域之一。這一部分我們將介紹動態模型重要的建模概念，如狀態空間、平衡態和穩定性。

首先，我們從一個簡單的例子開始，並輔以建模五步驟，來建立問題的動態模型。

範例

有一片林區，有兩種樹種，硬材樹與軟材樹。硬材樹的價值高但生長慢，軟材樹生長快；硬材樹有著高度的優勢，遮擋小樹陽光，更抗疾病，而軟材樹靠著有效消耗水分與土壤養分與硬材樹競爭。試問這兩種樹是否可無限期共存，亦或是一種樹迫使另一種是滅絕。

在一開始所做的假設要盡可能的簡單但不可忽略問題最基本的方面，隨後才逐步改進或複雜化這個模型。
1. 提出問題


2. 選擇模型方法
將問題建立成一個定常態的動態模型，定常態是指系統處於平衡點時，所有的變化率為0，亦即作用在系統上的全部影響達到平衡。因為達到平衡，未來的任何時刻系統都處於現在的狀態。
設函數



定義在的子集上，函數分別表示每個變量的變化率。若在點時，



則稱集合中的這一點為平衡點，也就是說，每個變量的變化率為0，系統處於靜止狀態。稱為狀態變數，為狀態空間。因為函數僅依賴系統的當前狀態，所以當前狀態完全確定系統的將來，而與過去無關。
3. 推導數學模型的數學表達式
令, ，狀態空間:
定常態方程式為


4. 求解模型
從步驟三的方程組可以解得四個點，如下圖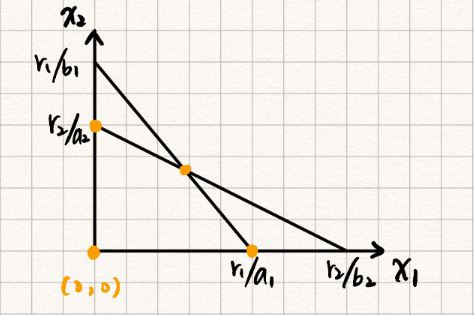

5. 表達分析結果
若要共存其條件為，每種樹達到限制自己增長的點之前，便已達到它限制另一種樹增長的點。