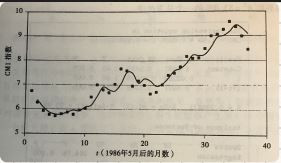
今天要介紹的是時間序列，它是一個隨時間變化的隨機過程，通常是在固定的時間區間上進行分析，例如每天的溫度和降雨量，每月的失業率以及年收入都是時間序列的一種，而分析時間序列資料的工具之一就是線性回歸。讓我們用昨天的例子以時間序列的方式再分析一次，看看有甚麼相異之處。

範例

對1986年6月到1989年6月的CM1指數的資料來估計1990年5月的CM1指數

1. 提出問題
   預測
2. 選擇建模方法
   使用時間序列模擬這個問題，並擬合一個自回歸模型，它假設在一個穩定的時間序列中加入一個趨勢，這趨勢是隨時間變化的非隨機函數。若和自相關係數在時間上是常數，則該時間序列被稱為是穩定的。
   自相關係數，，其中。
   因此，在此例中
   我們使用最簡單有用的模型自回歸過程，
   
   來模擬此模型，參數稱為自回歸過程的階。在這邊就會產生一個問題，如何選取合的值 關注的值，作法是將預測變項一個一個加入，直到的改善達到最小為止。
3. 推導模型的數學表達式
   考慮對某些常數和某個誤差，為了選擇適當的參數，可依序假設，代到模型中，直到取得滿意的結果，使得這模型具有不相關的殘差噪音序列且包括最少個數的預測變項。
4. 求解模型
   利用，解得。在此以的模型來求解
   ，對其取期望值
   
   將CM1的資料代入整理可得矩陣形式，
   
   解得
   故所求
   附上程式碼

   import numpy as np
   
   CM1 = [6.73,6.27,5.93,5.77,5.72,5.8,5.87,5.78,5.96,6.03,6.5,7,6.8,6.68,7.03,7.67,7.59,6.96,7.17,6.99,6.64,6.71,7.01,
       7.40,7.49,7.75,8.17,8.09,8.11,8.48,8.99,9.05,9.25,9.57,9.36,8.98,8.44]
   
   t = np.linspace(0, len(CM1)-1, len(CM1))
   
   # 簡單線性回歸
   A = []
   for i in t:
       temp = [1, i]
       A.append(temp)
   
   pinv_A = np.linalg.pinv(np.array(A))
   
   coef = pinv_A.dot(np.array(CM1).reshape(len(CM1),1))
   print(coef)
   
   # 自回歸
   self_A = []
   for i in t:
       if i == len(t) - 1:
           break
       temp = [1, i, CM1[int(i)]]
       self_A.append(temp)
   
   pinv_self_A = np.linalg.pinv(np.array(self_A))
   
   CM1.pop(0)
   
   self_coef = pinv_self_A.dot(np.array(CM1).reshape(len(CM1),1))
   print(self_coef)
   

5. 說明分析結果
   統計量表示此模型組合對該月CM1指數的預測有94.1%的變異解釋量，與昨天的簡單線性回歸模型的83%要來的好。
   下圖是使用自回歸模型所擬合出來的結果